BEM Integral and geometrical means in the analytical

BEM期末作業 Integral and geometrical means in the analytical evaluation of the BEM integrals for a 3 D Laplace equation 指導教授：陳正宗 學生：黃佳美 學號：M 98510007

Introduction l This paper focuses on the analytical evaluation of the surface integrals connected with the BEM procedure for the 3 D Laplace equation. l General formulas for constant approximation Planar polygons as boundary elements l – Evaluating the H-type integral l l The meaning of θ Bonnet integral formula

General formulas for constant approximation l For the Laplace equation l satisfied by u in a 3 D region with closed boundary S, the standard BEM procedure leads to the following equation:

Planar polygons as boundary elements l l a planar polygon without holes and self-intersections. denote its vertices by Pk, and their radius vectors by rk, where k=0, 1, 2, …. , K-1

Planar polygons as boundary elements l Evaluating the H-type integral

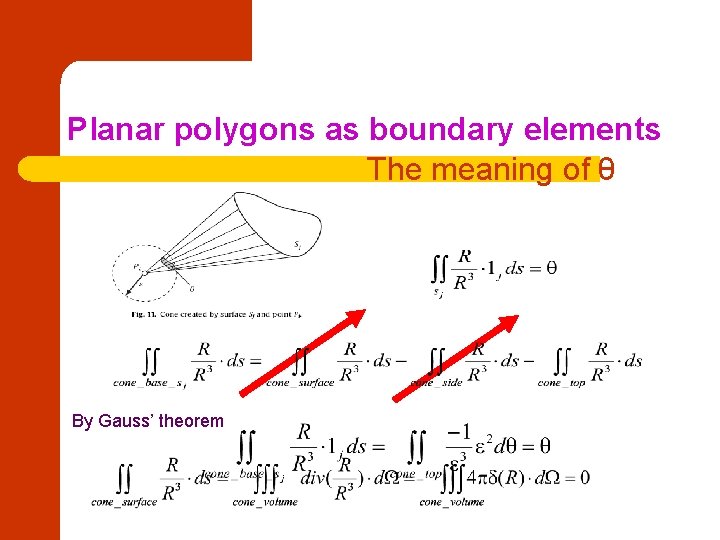
Planar polygons as boundary elements The meaning of θ By Gauss’ theorem

Planar polygons as boundary elements Bonnet integral formula

Planar polygons as boundary elements

Planar polygons as boundary elements

Planar polygons as boundary elements For convex polygons, all angles γk≧ 0 , Hence, we may disregard εk in the formula

Thanks for your attentions