BELLWORK Eureka Module 3 Lesson 16 Exercise 1

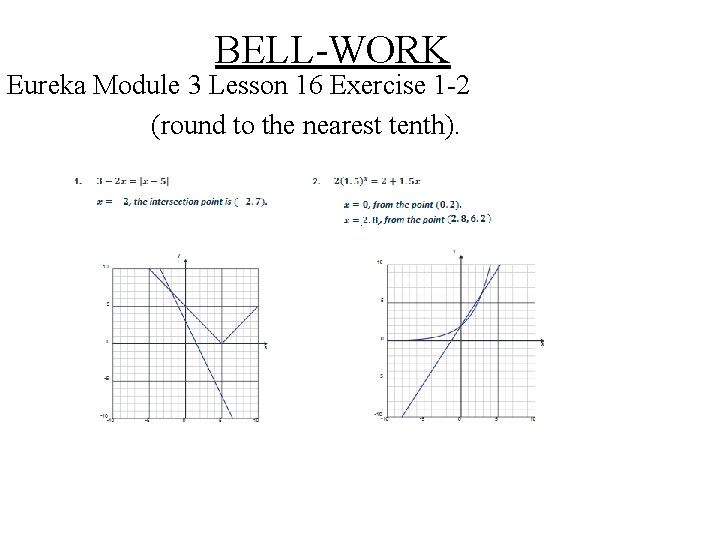
BELL-WORK Eureka Module 3 Lesson 16 Exercise 1 -2 (round to the nearest tenth).

Solving Inequalities in 1 Variable Now we will solve inequalities in 1 variable. Example: x + 2. 5 ≤ 8 x ≤ 5. 5 Notice that this inequality only has 1 variable, so we will graph its solution on a number line.

Solving and Graphing Inequalities Examples: x + 2. 5 ≤ 8 x ≤ 5. 5

Solving and Graphing Inequalities Examples: 5 t > 15 t>3

Solving and Graphing Inequalities Examples: w– 1<8 w<9

Solving and Graphing Inequalities Examples: 3≥p 4 12 ≥ p p ≤ 12

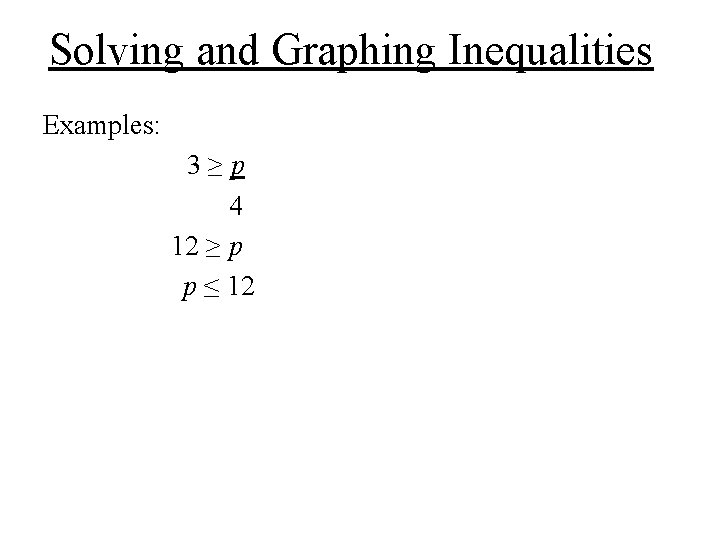
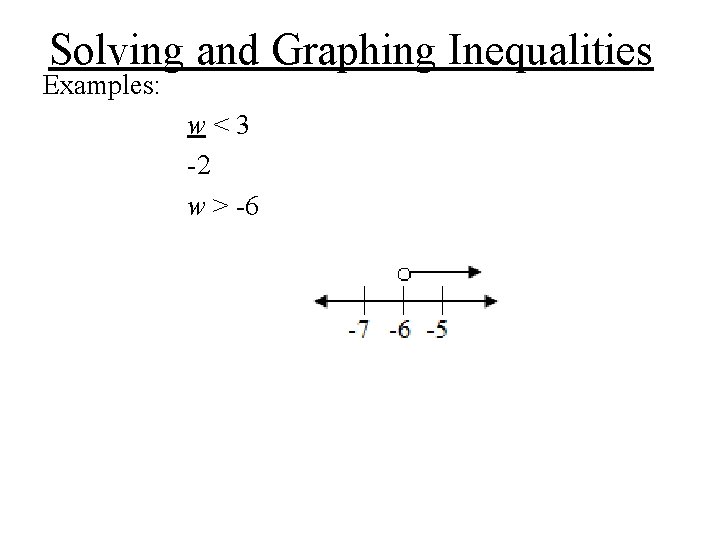
Solving and Graphing Inequalities Examples: w<3 -2 w > -6

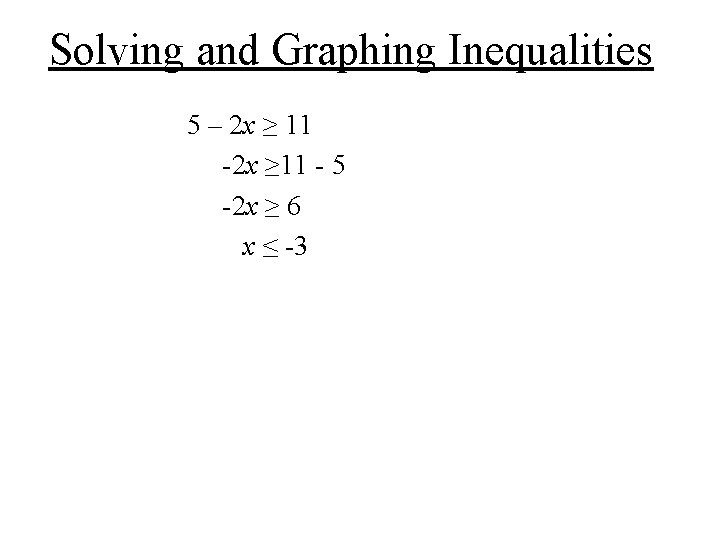
Solving and Graphing Inequalities 5 – 2 x ≥ 11 - 5 -2 x ≥ 6 x ≤ -3

Compound Inequalities What does the word compound mean? When two inequalities are joined, a compound inequality is formed. If the inequalities are joined by the word ‘and’ a conjunction is formed. Example: All real numbers that are at least -1 and at most 3. So, x ≥ -1 and x ≤ 3 Which is written as -1 ≤ x ≤ 3, and is graphed as:

Compound Inequalities What does the word compound mean? When two inequalities are joined, a compound inequality is formed. If the inequalities are joined by the word ‘and’ a conjunction is formed. Example: All real number that are at least -1 and at most 3. So, x ≥ -1 and x ≤ 3 Which is written as -1 ≤ x ≤ 3, and is graphed as:

Compound Inequalities What does the word compound mean? When two inequalities are joined, a compound inequality is formed. If the inequalities are joined by the word ‘and’ a conjunction is formed. Example: All real numbers that are at least -1 and at most 3. So, x ≥ -1 and x ≤ 3 Which is written as -1 ≤ x ≤ 3, and is graphed as: Notice there is no gap in the graph, which implies that solutions to a conjunction make both components of the conjunction true.

Compound Inequalities Write a compound inequality for the following: Today’s temperature will be no more than 70 degrees but it will be higher than 55. T ≤ 70 and T > 55 55 < T ≤ 70 Graph the solution.

Solving Conjunctions Solve and graph -4 < r – 5 ≤ -1 If this were just a regular inequality: r – 5 ≤ -1 how would you solve it? What ever is done to one side of a conjunction, must be done to all other sides. -4 < r – 5 ≤ -1 -4 + 5 < r ≤ -1 + 5 1<r≤ 4

Solving Conjunctions Solve and graph -4 < r – 5 ≤ -1 -4 + 5 < r ≤ -1 + 5 1<r≤ 4

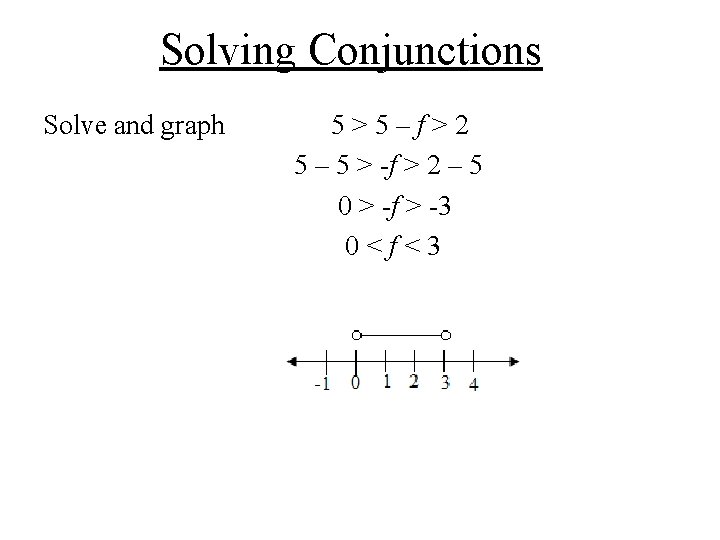
Solving Conjunctions Solve and graph 5>5–f>2 5 – 5 > -f > 2 – 5 0 > -f > -3 0<f<3

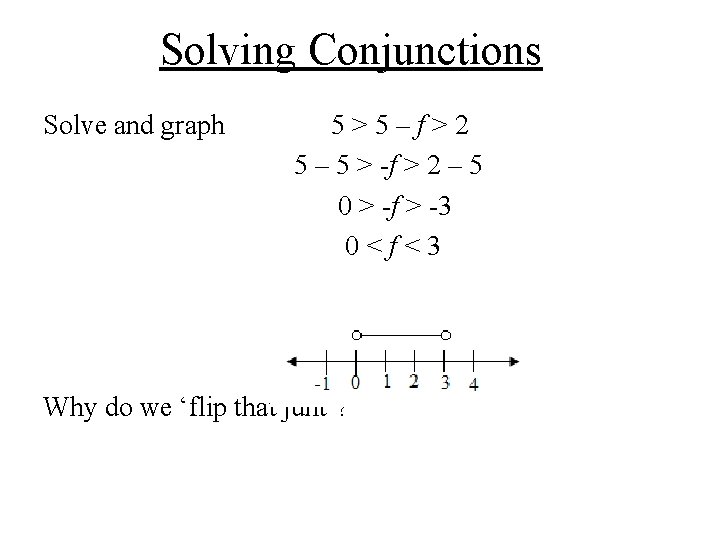
Solving Conjunctions Solve and graph 5>5–f>2 5 – 5 > -f > 2 – 5 0 > -f > -3 0<f<3 Why do we ‘flip that junt’?

Solving Conjunctions What are the solutions of 20 x – 18 < 50 < 36 x – 16? Notice that the variable is not in the middle! When that happens, the inequality must be broken into 2 parts: 20 x – 18 < 50 and 50 < 36 x – 16 x < 17 and x > 11 5 6 11 < x < 17 6 5