Bellwork 1 Write the equation for a line

Bellwork 1) Write the equation for a line that is parallel to the line y= ⅓x – 4. 2) Write the equation for a line that is perpendicular to the line y= ⅓x – 4.

6 -1 Classifying Quadrilaterals Geometry

Definitions: SIDE • Polygon—a plane figure that meets the following conditions: – It is formed by 3 or more segments called sides, such that no two sides with a common endpoint are collinear. – Each side intersects exactly two other sides, one at each endpoint. • Vertex – each endpoint of a side. Plural is vertices. You can name a polygon by listing its vertices consecutively. For instance, PQRST and QPTSR are two correct names for the polygon above.

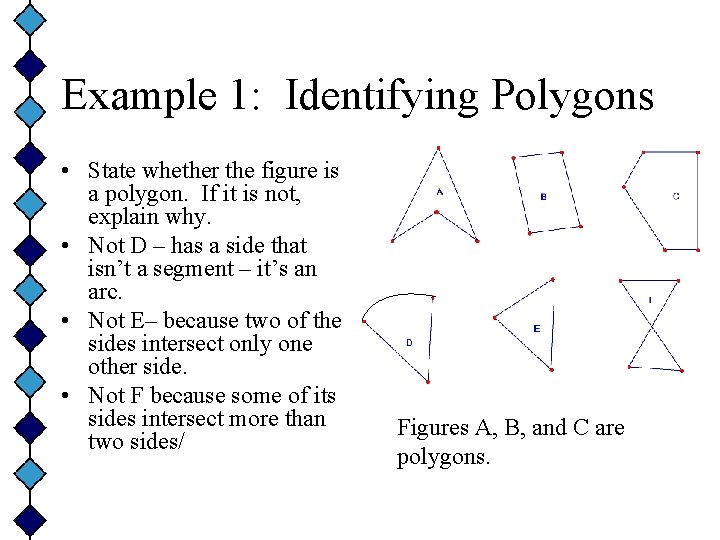
Example 1: Identifying Polygons • State whether the figure is a polygon. If it is not, explain why. • Not D – has a side that isn’t a segment – it’s an arc. • Not E– because two of the sides intersect only one other side. • Not F because some of its sides intersect more than two sides/ Figures A, B, and C are polygons.

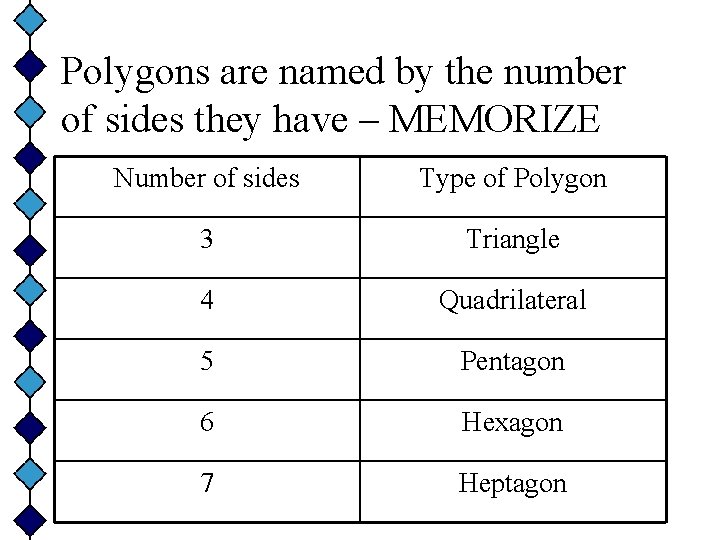
Polygons are named by the number of sides they have – MEMORIZE Number of sides Type of Polygon 3 Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon

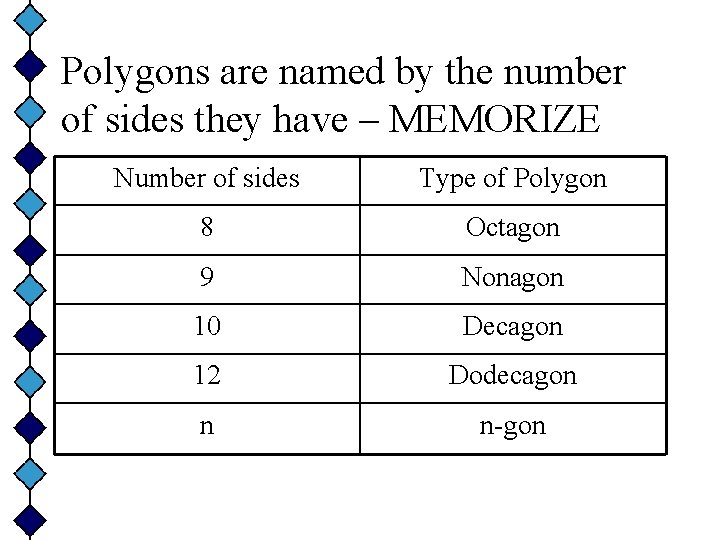
Polygons are named by the number of sides they have – MEMORIZE Number of sides Type of Polygon 8 Octagon 9 Nonagon 10 Decagon 12 Dodecagon n n-gon

Convex or concave? • Convex if no line that contains a side of the polygon contains a point in the interior of the polygon. • Concave or non-convex if a line does contain a side of the polygon containing a point on the interior of the polygon. See how this crosses a point on the inside? Concave. See how it doesn’t go on the Inside-- convex

Convex or concave? • Identify the polygon and state whether it is convex or concave. A polygon is EQUILATERAL If all of its sides are congruent. A polygon is EQUIANGULAR if all of its interior angles are congruent. A polygon is REGULAR if it is equilateral and equiangular.

Types of Quadrilaterals 1) Parallelogram- a quadrilateral with both pairs of opposite sides parallel.

Types of Quadrilaterals 2) Rhombus- a parallelogram with four congruent sides.

Types of Quadrilaterals 3) Rectangle- A parallelogram with four right angles.

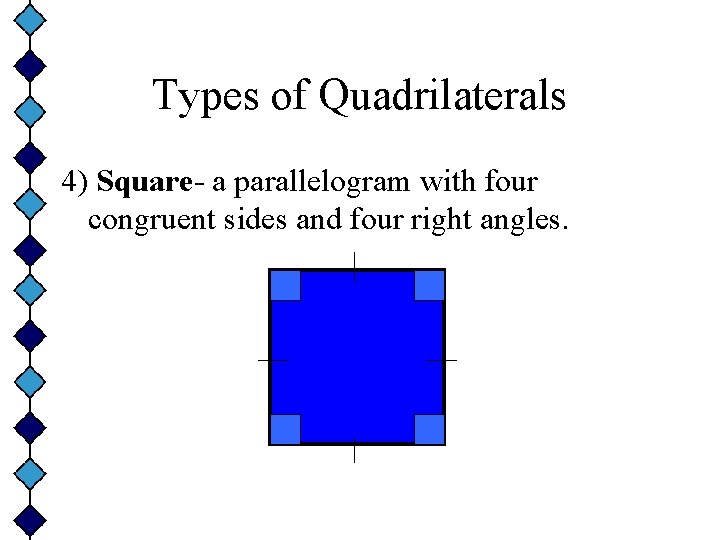
Types of Quadrilaterals 4) Square- a parallelogram with four congruent sides and four right angles.

Types of Quadrilaterals Trapezoid- Quadrilateral with exactly one pair of parallel sides. Isosceles Trapezoid- a trapezoid whose non parallel opposite sides are congruent.

Types of Quadrilaterals 5) Kite- Quadrilateral with two pairs adjacent sides congruent and no opposite sides congruent

Identifying Regular Polygons • Remember: Equiangular & equilateral • Decide whether the following polygons are regular. Equilateral, but not equiangular, so it is NOT a regular polygon. Heptagon is equilateral, but not equiangular, so it is NOT a regular polygon. Pentagon is equilateral and equiangular, so it is a regular polygon.

EX. Find the values of the variables of the kite 2 x + 4 x+6 3 x - 5 2 y + 5

On your own!!!!! Find the values for the variables and then find the length of the sides. 3 f+2 g +6 2 g -5 5 f-8

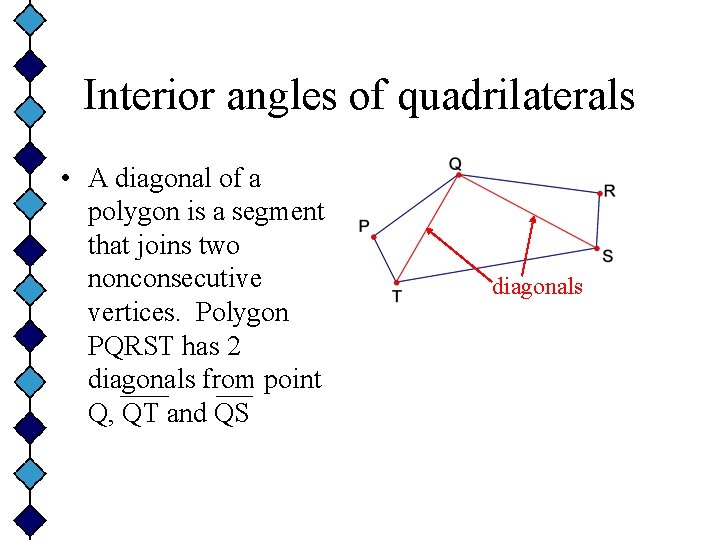
Interior angles of quadrilaterals • A diagonal of a polygon is a segment that joins two nonconsecutive vertices. Polygon PQRST has 2 diagonals from point Q, QT and QS diagonals

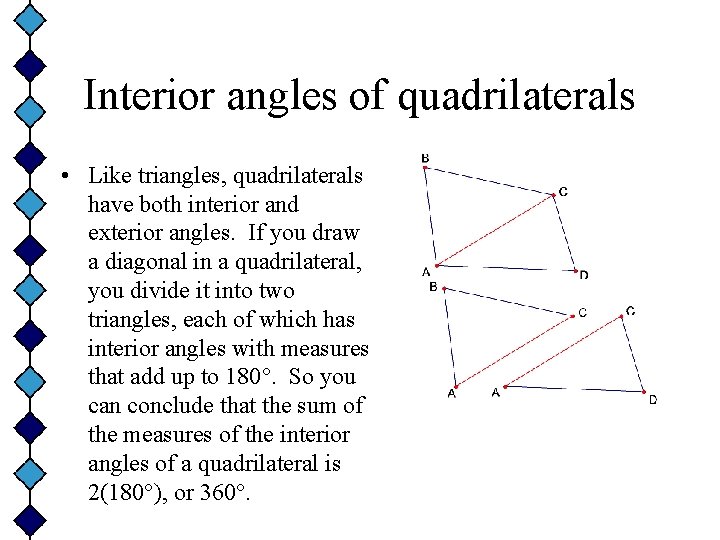
Interior angles of quadrilaterals • Like triangles, quadrilaterals have both interior and exterior angles. If you draw a diagonal in a quadrilateral, you divide it into two triangles, each of which has interior angles with measures that add up to 180°. So you can conclude that the sum of the measures of the interior angles of a quadrilateral is 2(180°), or 360°.

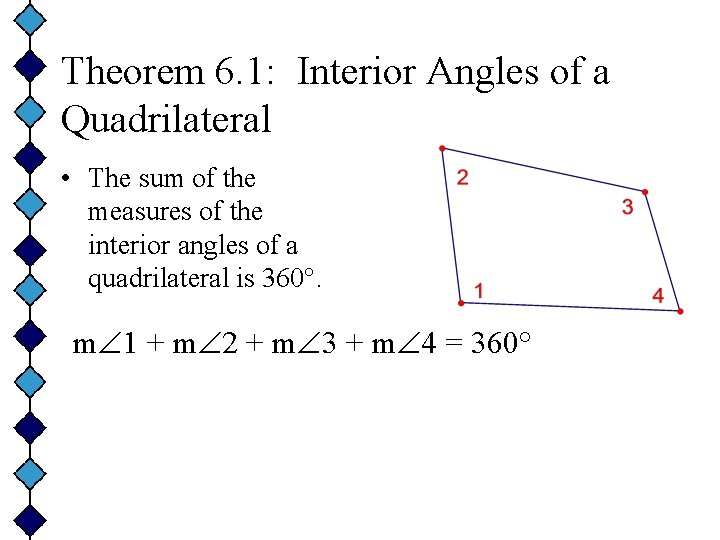
Theorem 6. 1: Interior Angles of a Quadrilateral • The sum of the measures of the interior angles of a quadrilateral is 360°. m 1 + m 2 + m 3 + m 4 = 360°

Ex. 4: Interior Angles of a Quadrilateral • Find m Q and m R. • Find the value of x. Use the sum of the measures of the interior angles to write an equation involving x. Then, solve the equation. Substitute to find the value of R. 80° 70° x° 2 x° x°+ 2 x° + 70° + 80° = 360°

Ex. 4: Interior Angles of a Quadrilateral x° x°+ 2 x° + 70° + 80° = 360° 3 x + 150 = 360 3 x = 210 x = 70 80° 70° 2 x° Sum of the measures of int. s of a quadrilateral is 360° Combine like terms Subtract 150 from each side. Divide each side by 3. Find m Q and m R. m Q = x° = 70° m R = 2 x°= 140° ►So, m Q = 70° and m R = 140°