Bellwork 1 Classify the angle 2 Construct a

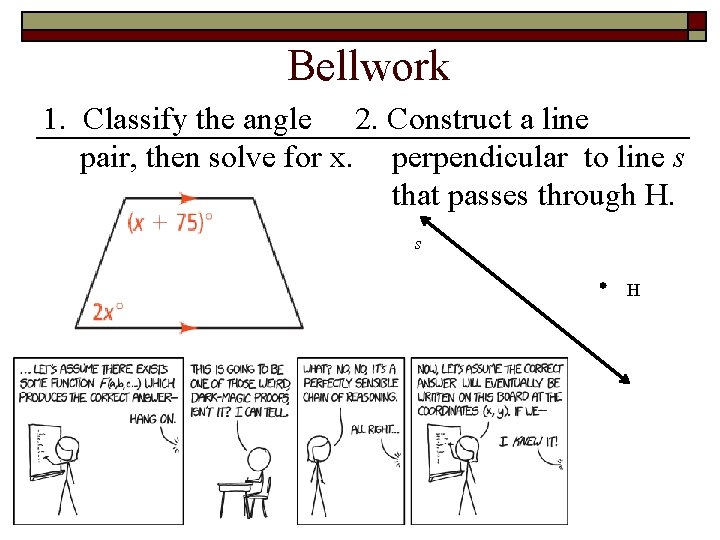
Bellwork 1. Classify the angle 2. Construct a line pair, then solve for x. perpendicular to line s that passes through H. s H

Lesson 3 -3 & 3 -4: Parallel & Perpendicular Line Theorems Rigor – Prove lines are parallel or perpendicular; determine the value of x that will make lines parallel Relevance – logical thinking, construction

Recap: Theorems vs Converses o The angle pair THEOREMS: n n o Given - lines are parallel Conclusion – angle pairs are supplementary Angle pair CONVERSES: n n Given - angle pairs are or supplementary Conclusion – lines are parallel or

Example 1: Which lines are parallel? Justify your answer. o

Example 2: Applying the Converse What value of x would make the lines parallel? a) b)

Theorems to know: o o Perpendicular Transversal Theorem If a transversal is perpendicular to 1 of 2 parallel lines, then it is perpendicular to the other line. Corollary to the Corresponding Angles Converse – If 2 coplanar lines are perpendicular to the same line, then they are parallel to each other.

Theorems to know continued:

Example 3

Proof of the ⊥ Transversal Theorem o Reasons 1. ________ 2. ________________ 3. 4. Definition of congruent 5. _________________ 6.

3 -3 and 3 -4 Assignment Worksheet o Whatever you don’t finish in class is homework. o Due Tuesday 11/1 for periods 2, 4, & 6 Due Thursday 11/3 for periods 1, 5, & 7 o