Bellringer Graph the functions below Identify the vertex

Bell-ringer Graph the functions below. Identify the vertex, axis of symmetry, whether it opens up or down and whether it has a maximum or a minimum value. g(x) = -3 x 2 +6 x +4 opens down, max; (1, 7), x = 1. f(x) = x 2 + x – 1 opens up; min; (0, -1); x = 0

Graphs for bell-ringer

7. 2 Polynomial Functions & Their Graphs

Definitions When a function rises and then falls over an interval from left to right, the function has a local maximum. If the function falls and then rises over an interval from left to right, it has a local minimum. Think about a rollercoaster!

Increasing and Decreasing Functions The points on the graph of a polynomial function that correspond to local maxima and local minima are called turning points. Functions change from increasing to decreasing or from decreasing to increasing at turning points. A polynomial has at most one less turn or turning point than its degree.

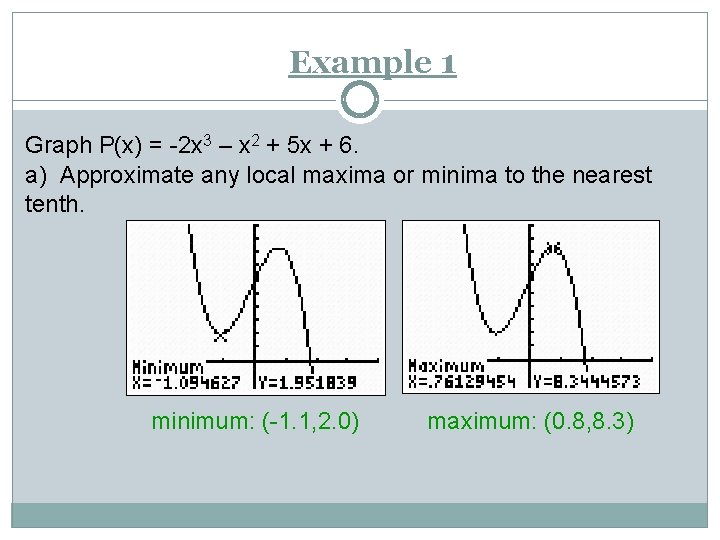
Example 1 Graph P(x) = -2 x 3 – x 2 + 5 x + 6. a) Approximate any local maxima or minima to the nearest tenth. minimum: (-1. 1, 2. 0) maximum: (0. 8, 8. 3)

Now You Use the graphing calculator to approximate the local maxima and local minima. f(x) = -2 x 3 - x 2 + 5 x + 6. Local max (0. 8, 8. 3), local min (-1. 1, 2. 0)

Exploring End Behavior Activity Page 435 and additional worksheet You may work in groups of two or three. Complete the table and answer all questions.

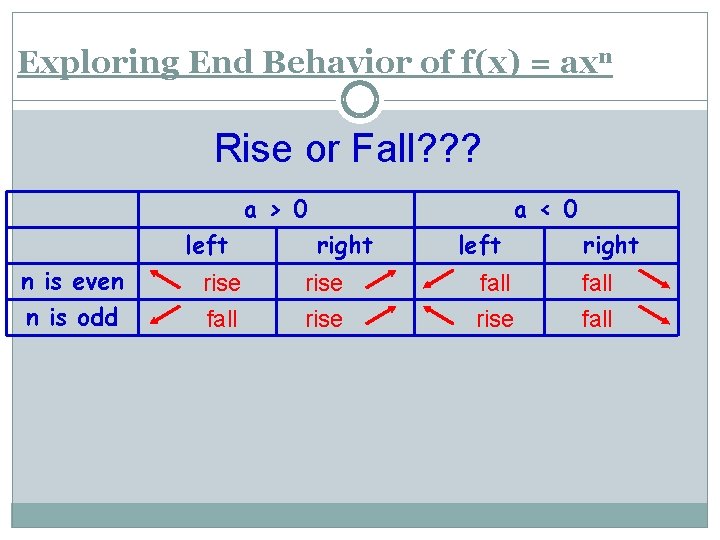
Exploring End Behavior of f(x) = axn Rise or Fall? ? ? a > 0 left n is even n is odd rise fall a < 0 right rise left fall rise right fall

End Behavior Summary When the degree of the function is odd and the leading coefficient is positive, the graph falls on the left and rises on the right When the degree of the function is odd and the leading coefficient is negative, the graph rises on the left and falls on the right When the degree of the function is even and the leading coefficient is positive, the graph rises on the left and the right. When the degree of the function is even and the leading coefficient is negative, the graph falls on the left and on the right.

Example 2 Describe the end behavior of the function 1). V(x) = 1 - x 3 + x - x 2 + 2 x 4 Rises on the left and rises on the right 2). P(x) = -6 x 2 + x 3 + 32 Falls on the left and rises on the right

Example 3 Graph the function, approximate any local maxima/minima to the nearest tenth, and describe the end behavior of the function. f(x) = x 4 - 4 x 3 +3 x + 5. Local min (-. 5, 4. 1), (2. 9, -13. 1); local max (. 6, 6. 1) the graph rises on the left and right

Now You Graph the function, approximate any local maxima/minima to the nearest tenth, and describe the end behavior of the function. f(x) = 2 x 3 - 3 x 2 - 6 x – 5 Local max (-. 6, -2. 9) local min (1. 6, -14. 1) falls on the left and rises on the right

Check Your Understanding On a piece of scratch paper, summarize how end behavior and local maxima and minima can be used to sketch the graph of a polynomial function.

Homework Page 438 #10 -18 even, 30 -36 even