Bell Work Copy the reflection and rotation chart

Bell Work • Copy the reflection and rotation chart 2 times each!!!!! You can put it in your 3. 1 notes!

3. 2 Proving Figures are Congruent Using Rigid Motions Essential Question: How can you determine whether two figures are congruent?

Two plane figures are congruent if and only if one can be obtained from the other by a sequence of rigid motions (that is, by a sequence of reflections, translations, and/or rotations).

Remember, in order for 2 figures to be congruent to each other they must have the same size and shape!

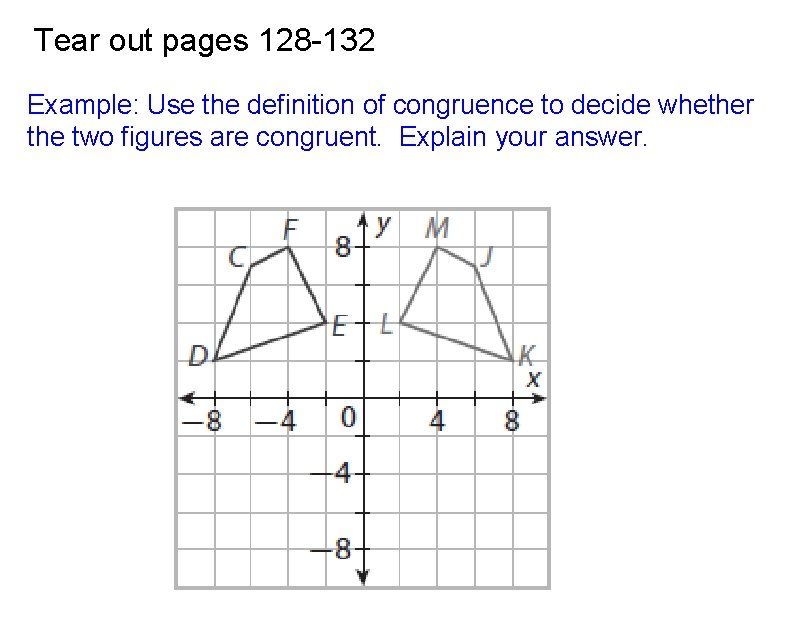
Tear out pages 128 -132 Example: Use the definition of congruence to decide whether the two figures are congruent. Explain your answer.

Example: Use the definition of congruence to decide whether the two figures are congruent. Explain your answer. Since the 2 figures appear to be the same size and shape, we must look for a rigid transformation that will map one to the other. There is a reflection across the y-axis that maps CDEF to JKLM.

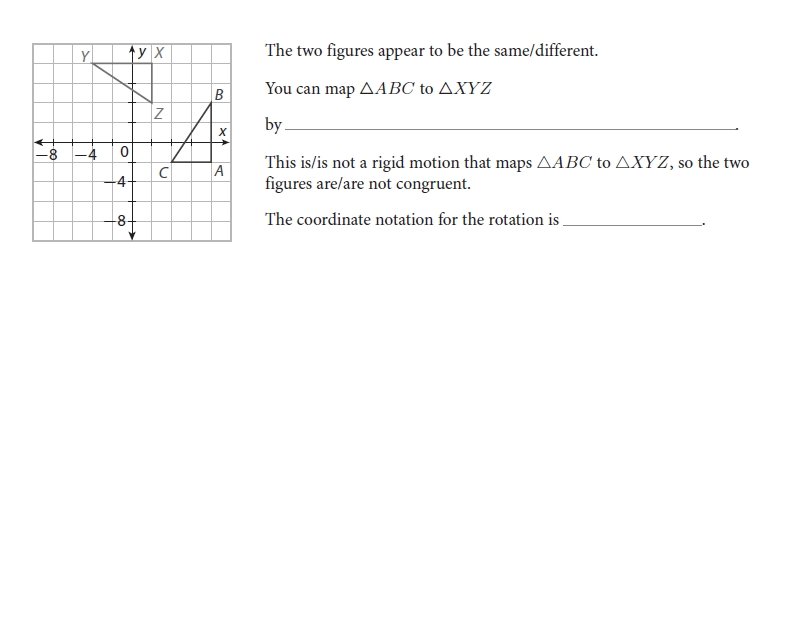
The figures shown are congruent. Find a sequence of rigid motions that maps one figure to the other. Give coordinate notation for the transformations you use. Preimage Image Rotation: _____ Translation: ____

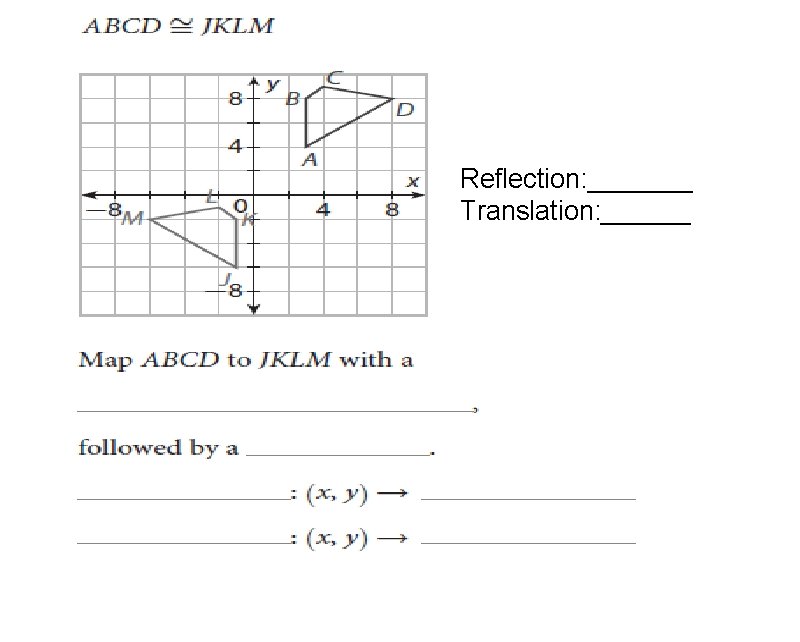
Reflection: _______ Translation: ______

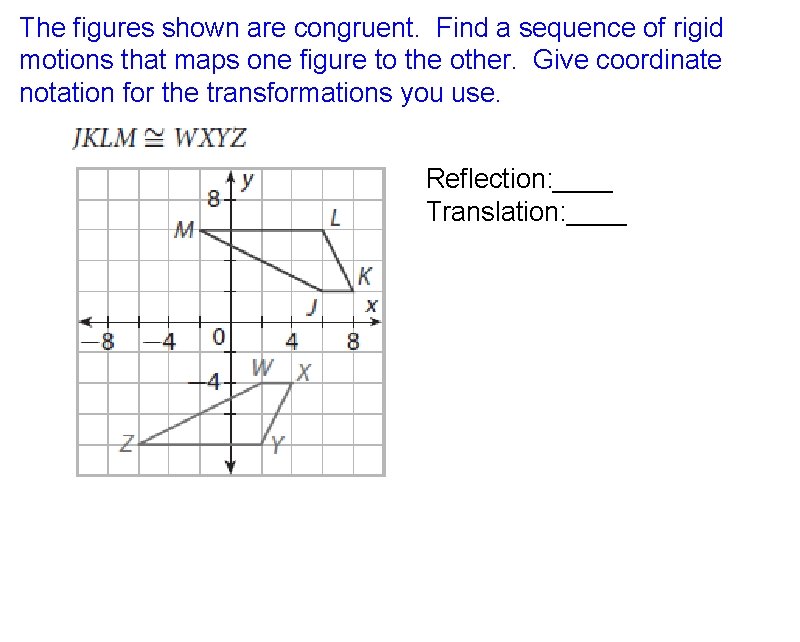
The figures shown are congruent. Find a sequence of rigid motions that maps one figure to the other. Give coordinate notation for the transformations you use. Reflection: ____ Translation: ____

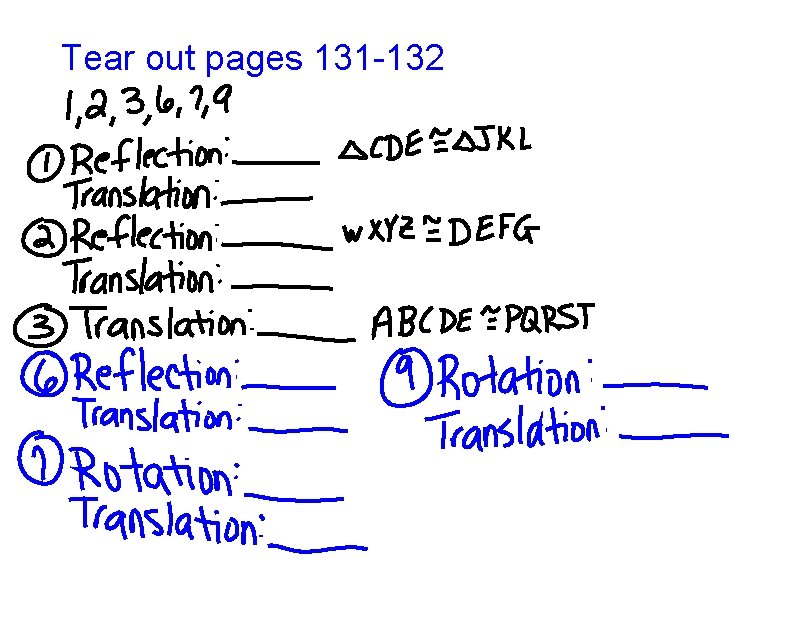
Tear out pages 131 -132

Answers: 1. Reflection: x axis; (x, -y) Translation: <8, 0> 2. Reflection: x axis; (x, -y) Translation: <10, 0> 3. Translation: <-2, -7> 6. Reflection: y axis; (-x, y) Translation: <1, -4> 7. Rotation: 180; (-x, -y) Translation: <2, 6> 9. Rotation: 180; (-x, -y) Translation: <-2, 0>