Bell Work 1 A Write a similarity statement

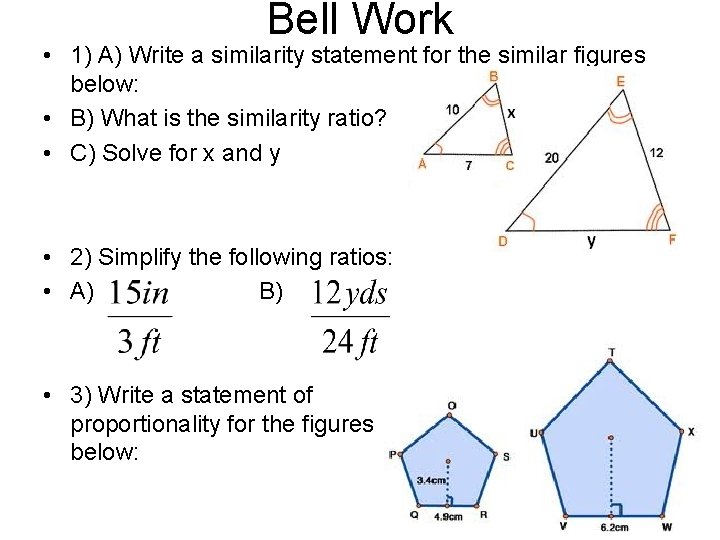
Bell Work • 1) A) Write a similarity statement for the similar figures below: • B) What is the similarity ratio? • C) Solve for x and y • 2) Simplify the following ratios: • A) B) • 3) Write a statement of proportionality for the figures below:

Agenda • • • 1) Bell Work 2) IP Check 3) Outcomes 6) 8. 4 Notes 7) IP – Assessment #11

Outcomes • I will be able to: • 1) Use ratios and proportions to find missing side lengths of similar figures • 2) Determine if triangles are similar • 3) Use similarity shortcuts to determine if triangles are similar

Similar Triangle Activity 1. Look at Triangle ABC and Triangle DEF: Ø A (1, 1) and D (1, -1) Ø B (4, 1) E (7, -1) Ø C (4, 5) F (7, -9) Are these triangles similar? Yes/No Why? 2. Look at Triangle JKL and Triangle MNO: Ø J (1, 2) and M (-1, -1) Ø K (5, 2) N (-3, -1) Ø L (3, -2) O(-2, -3) __________ 3. Look at Triangle PQR and Triangle STV: Ø P (-2, 0) and S (-1, 1) Ø Q (0, 4) T (0, 3) Ø R (2, 0) V (1, 1) Similarity Statement: Statement of Proportionality? _________ What pieces did we need to determine similarity?

Results • 1. Look at Triangle ABC and Triangle DEF where: • A (1, 1) and D (1, -1) • B (4, 1) E ((7, -1) • C (4, 5) F (7, -9) • AB = ______ • DE = ______ • m∠A = ___, m∠D= ____ • AC = _____ • DF = ______ • Are these triangles similar? Yes/No • Why? • Similarity Statement: __________ Statement of Proportionality? _________ • What pieces did we need to determine similarity?

Results • 2. Look at Triangle JKL and Triangle MNO where: • J (1, 2) and M (-1, -1) • K (5, 2) N (-3, -1) • L (3, -2) O (-2, -3) • Are these triangles similar? Yes/No • Why? • Similarity Statement: __________ Statement of Proportionality? _________ • What pieces did we need to determine similarity?

Results • 3. Look at Triangle PQR and Triangle STV where: • P (-2, 0) and S (-1, 1) • Q (0, 4) and T (0, 3) • R (2, 0) and V (1, 1) • Are these triangles similar? Yes/No • Why? • Similarity Statement: __________ Statement of Proportionality? • PQ = ____ ST =_____ • QR = ____ TV = ____ • RP = _____ VS= ___________ • What pieces did we need to determine similarity?

Why? • What did we find during this activity? • Did we need to look at every single and every single side to determine if the triangles were similar? • No, so there are triangle similarity shortcuts just as there were triangle congruence shortcuts.

Shortcuts • Just as when looking at triangle congruence, there are shortcuts to help us determine if triangles are *similar.

Similar Triangles If Two angles of one triangle are congruent to two angles in another triangle, then the two triangles are similar. Why do we only need two angles? Similarity Statement:

Examples • 1) Explain why the triangles are similar and write a similarity statement B • • • Angle A is congruent to Angle D Angle C is congruent in both triangles A because of vertical angles So, by AA C D E

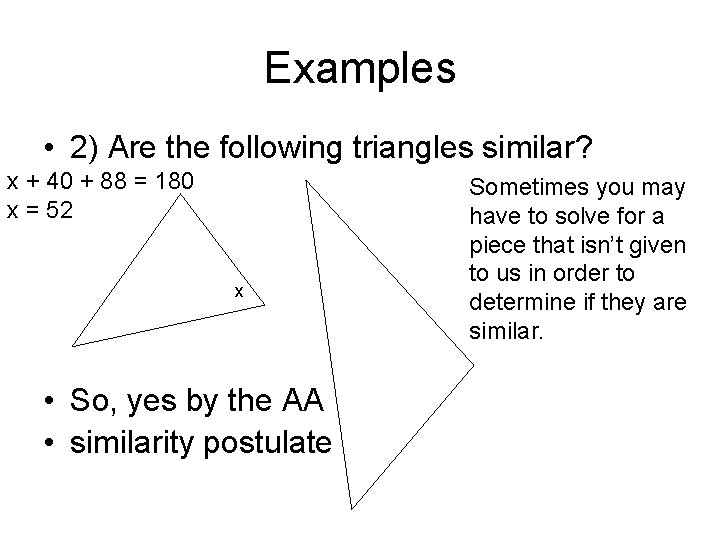
Examples • 2) Are the following triangles similar? x + 40 + 88 = 180 x = 52 x • So, yes by the AA • similarity postulate Sometimes you may have to solve for a piece that isn’t given to us in order to determine if they are similar.

On Your Own • 3. Explain why the triangles are similar and write a similarity statement • ΔRQP ~ ΔVUP by the AA postulate because: • Suppose RP = 15, RQ = 10 and UV = 7 • Find VP and RV 15 • What is the scale factor? 10 x 7 • Write a proportion to • solve:

Similarity Theorems If all the lengths of the corresponding sides 14 of two triangles are proportional, then the triangles are similar. 10 5 7 18 9 *Check the side ratios: 16 95° 12 If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar *Check the side ratios and the angle between them 8 95° 6

Examples 18 What should we do first? 1. Label everything What do we need to do next? 2. Look at what pieces of each triangle we actually have We have two sides from each so we can compare side ratios 6 4 12 So, we know two side ratios are the same. What else do we know? Both triangles have Angle A, so it is congruent So, these triangles are similar by SAS similarity shortcut

On Your OWN

Examples 1. Label what we know 2. Set up a proportion to find the missing piece. 60 48 x 40 52 65 What do we have to make sure we do? Compare pieces of the small triangle with pieces of the big triangle 48 x = 4320 x = 90 m

Examples 1. Label what we know 2. What can we check? ***Be sure to create a proportion in which the corresponding parts line up

On Your Own