Bell Ringer Plot each point on graph paper
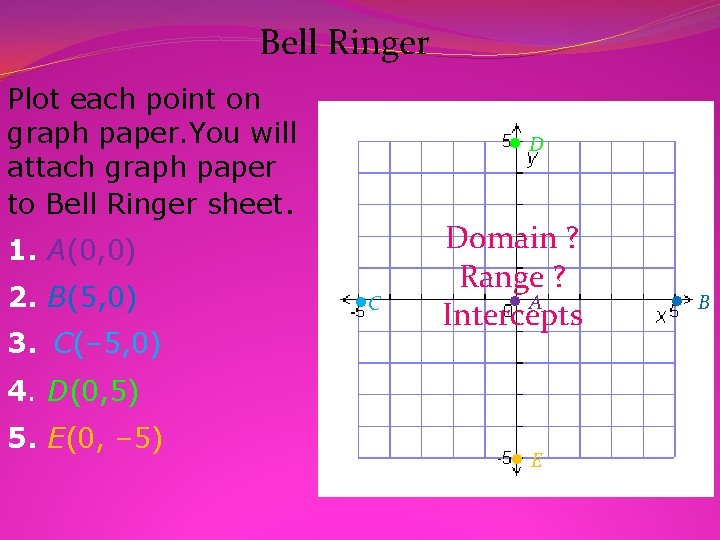
Bell Ringer Plot each point on graph paper. You will attach graph paper to Bell Ringer sheet. D 1. A(0, 0) 2. B(5, 0) 3. C(– 5, 0) C Domain ? Range ? A Intercepts 4. D(0, 5) 5. E(0, – 5) E B


Chapter 1 (1) Apply transformations to different families of functions. (2) Fit data to linear models. Holt Mc. Dougal Common Core Edition 1. 1 1. 4 F-IF. 6 A-REI. 1 F-BF. 3

Chapter 1 Vocabulary: suggestion: pick one color per word and definition. Co Rin py w ger ord on s fo r B she ell R Bell ing et er Correlation ate Slope D 1 t es , T 28 : e Reflection Du Regression Stretch Transformation vs. Translation Parent Function th
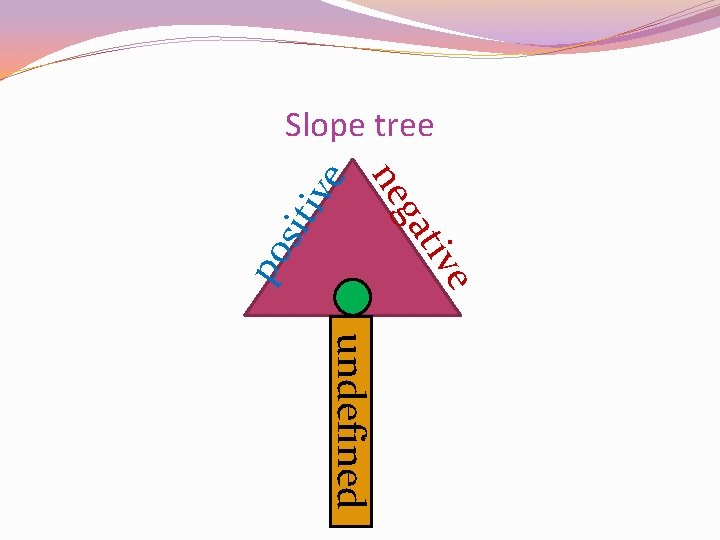
ga ive ne e tiv po sit Slope tree undefined

Example: Translating Points Perform the given translation on the point (– 3, 4). Give the coordinates of the translated point. 5 units right Translating (– 3, 4) 5 units right results in the point (2, 4). (-3, 4) (2, 4) ? Slope ? ? Domain ? ? Range ?

Example: Translating Points Perform the given translation on the point (– 3, 4). Give the coordinates of the translated point. 2 units (– 3, 4) 2 units left and 3 units down Translating (– 3, 4) 2 units left and 3 units down results in the point (– 5, 1). 3 units (– 5, 1)

Example: Translation Perform the given translation on the point (– 1, 3). Give the coordinates of the translated point. 4 units right Translating (– 1, 3) 4 units right results in the point (3, 3). (– 1, 3) (3, 3) ? Slope ?

Example: Translation Perform the given translation on the point (– 1, 3). Give the coordinates of the translated point. 1 unit left and 2 units down Translating (– 1, 3) 1 unit left and 2 units down results in the point (– 2, 1). 1 unit 2 units (– 1, 3) ? Slope ? (– 2, 1)

Notice that when you translate left or right, the x-coordinate changes, and when you translate up or down, the y-coordinate changes. Translations Horizontal Translation Vertical Translation

Bell Ringer Using complete sentence, correlate the “h” and “k” to “x” and “y”. Translations Horizontal Translation Vertical Translation

vocabulary ACT You can transform a function by transforming its ordered pairs. When a function is translated or reflected, the original graph and the graph of the transformation are congruent because the size and shape of the graphs are the same.
Activity Start 4 page packet You need to be responsible and keep up with it We will work on each day It is not homework yet

Exit Question You graphed y=x on a graphing calculator by pressing y= and entering y 1=x. Then pressed graph. Then you entered and graphed y 2 = x + 5. Next you entered and graphed y 3= x – 5. Exit Question: How does the term congruent explain how a change in the value of k in the equation y=x + k affects the equation’s graph.

Bell Ringer On graph paper. You may use the same piece from yesterday’s Bell Ringer. Perform the given translation on the point (-3, 4). Indicate the coordinates of the translated point. This is two different translations. a) 5 units right b) 2 unit left and 2 units down

Reflections Reflection Across y-axis Reflection Across x-axis
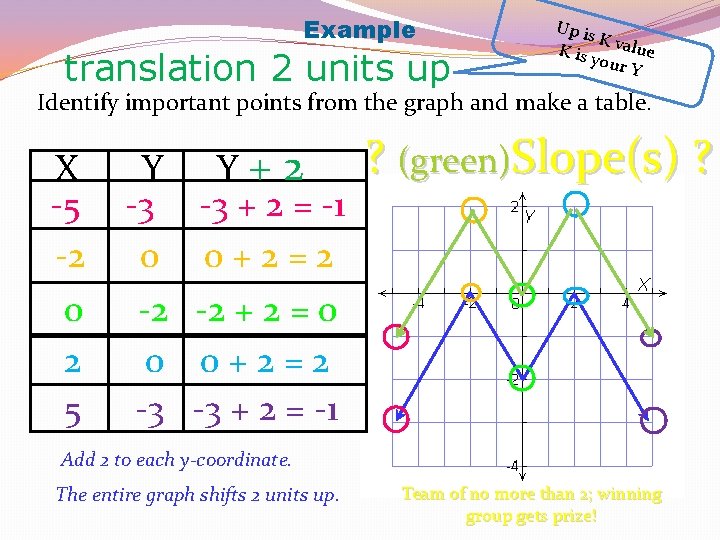
Example translation 2 units up Up is K K is y value our Y Identify important points from the graph and make a table. X -5 -2 0 2 5 Y -3 0 -2 0 -3 Y+2 -3 + 2 = -1 0+2=2 -2 + 2 = 0 0+2=2 -3 + 2 = -1 ? (green)Slope(s) ? Add 2 to each y-coordinate. The entire graph shifts 2 units up. Team of no more than 2; winning group gets prize!
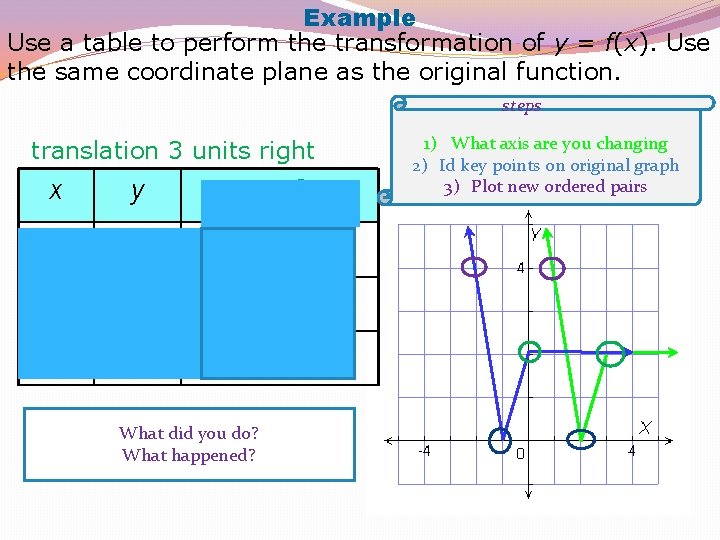
Example Use a table to perform the transformation of y = f(x). Use the same coordinate plane as the original function. steps translation 3 units right x y x+3 – 2 4 – 2 + 3 = 1 – 1 0 – 1 + 3 = 2 0+3=3 Add 3 to each x-coordinate. What did you do? The entire graph shifts 3 units right. What happened? 1) What axis are you changing 2) Id key points on original graph 3) Plot new ordered pairs
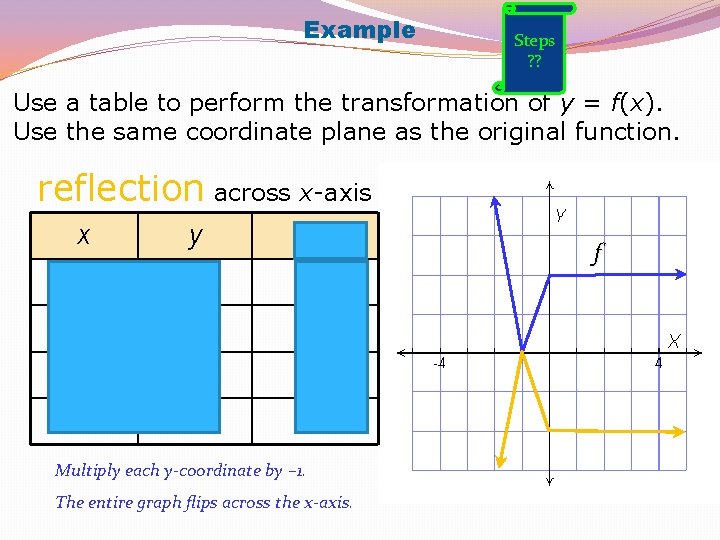
Example Steps ? ? Use a table to perform the transformation of y = f(x). Use the same coordinate plane as the original function. reflection across x-axis x y –y – 2 4 – 1 0 0 0 2 – 2 2 2 – 2 Multiply each y-coordinate by – 1. The entire graph flips across the x-axis. f
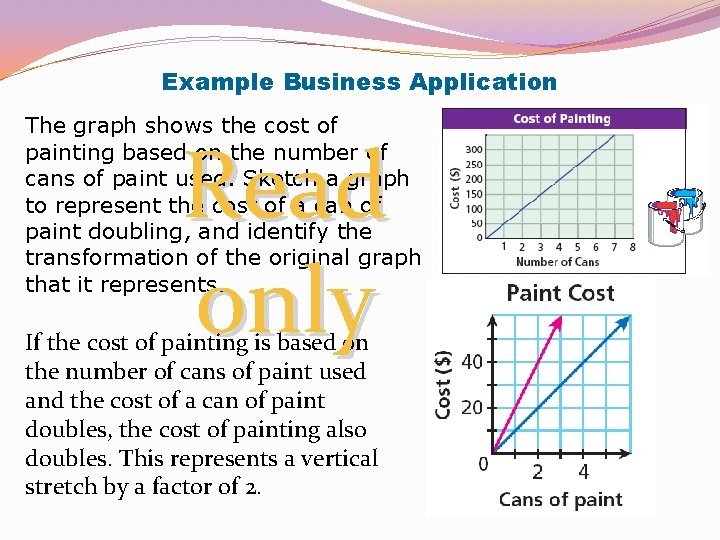
Example Business Application The graph shows the cost of painting based on the number of cans of paint used. Sketch a graph to represent the cost of a can of paint doubling, and identify the transformation of the original graph that it represents. Read only If the cost of painting is based on the number of cans of paint used and the cost of a can of paint doubles, the cost of painting also doubles. This represents a vertical stretch by a factor of 2.

Application: Chess Translation, one per team of two homework: finish packet, due tomorrow
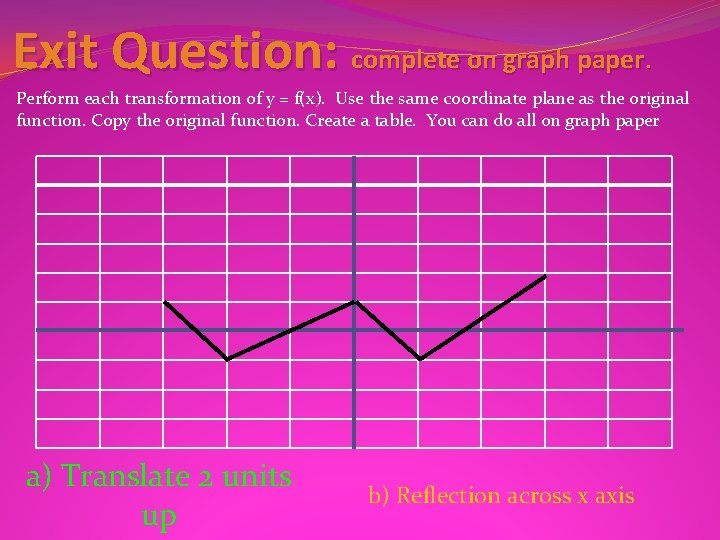
Exit Question: complete on graph paper. Perform each transformation of y = f(x). Use the same coordinate plane as the original function. Copy the original function. Create a table. You can do all on graph paper a) Translate 2 units up b) Reflection across x axis
- Slides: 22