BELL RINGER 5242010 1 What is the value
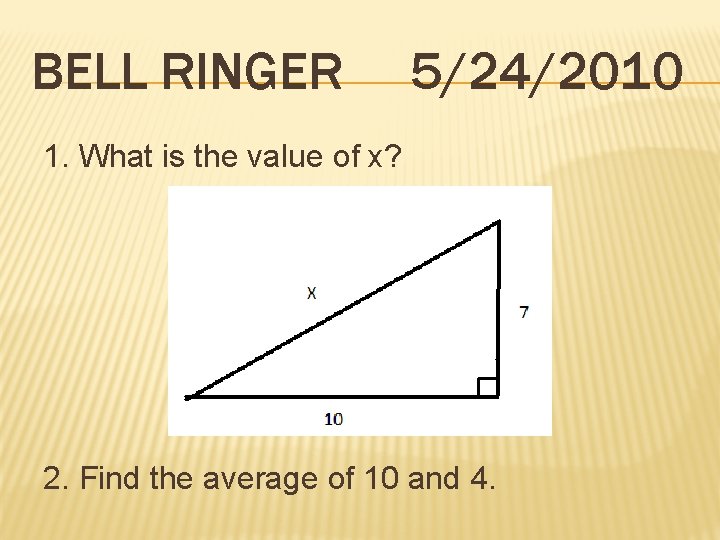
BELL RINGER 5/24/2010 1. What is the value of x? 2. Find the average of 10 and 4.

TODAY: MIDPOINT AND DISTANCE FORMULAS Lesson: 7. 6 Day 1 Activity Part 1: Record the coordinates of the endpoints of each segment. Using the cm side of a ruler, measure each segment. Place a dot in the middle of each segment and record the coordinates of the point. Measure carefully! Record your data on the page titled, “Part I Midpoint”.


Summary: Given any two points The midpoint formula is:

MIDPOINT FORMULA Find the midpoint of segment EF, given that E(-5, 7) and F(7, 5). Find the midpoint of segment RO, given that R(2, 0) and O(-8, 10).

PART II : DISTANCE FORMULA Part II: Using the segments below, create a series of right triangles (The first one has been done for you). Label the vertex of the RIGHT ANGLE “P”. None of the triangles should overlap. Determine the length of the segments that you drew. Use Pythagorean Theorem to find the length of the original segment. Record your data on the page titled “Part II Distance”.

PART II – DISTANCE AP = 6 cm BP = 10 cm AB Length: _______ cm CP = _______ cm DP = _______ cm CD Length: _______ cm EP = _______ cm FP = _______ cm EF Length: _______ cm GP = _______ cm HP = _______ cm GH Length: _______ cm IP = _______ cm JP = _______ cm IJ Length: _______ cm KP = _______ cm LP = _______ cm KL Length: _______ cm

Summary : Given any two points The distance formula (length of segment joining the two points) is derived by the Pythagorean theorem and is:

DISTANCE FORMULA Find the length of segment BE, given that B(6, 9) and E(6, -7).

Midpoint and Distance Formula Worksheet Find the coordinates of the midpoint of the segment joining the given points. 1. (0, 2) and (6, 4) 2. (-2, 2) and (6, 4) 3. (6, -7) and (-6, 3) 4. (-11, 3) and (8, -7) 5. (2. 3, 3. 7) and (1. 5, -2. 9) 6. (x, 2) and (x+4, -4)

Find the distance between the two points. 7. (-4, 2) and (2, -1) 8. (-2, -3) and (-2, 4) 9. (3, 2) and (5, -2) 10. (5, -7) and (8, -2)
- Slides: 11