Belief Propagation in Large Highly Connected Graphs for

Belief Propagation in Large, Highly Connected Graphs for 3 D Part-Based Object Recognition Frank Di. Maio and Jude Shavlik Computer Sciences Department University of Wisconsin – Madison USA

Part-Based Object Recognition l A part-based model describes an object using a pairwise Markov Field (Felzenszwalb et al 2000, Sudderth et al 2004, Isard 2003) l Object described using l Undirected part graph G=(V, E) l Vertex potential functions l Edge potential functions
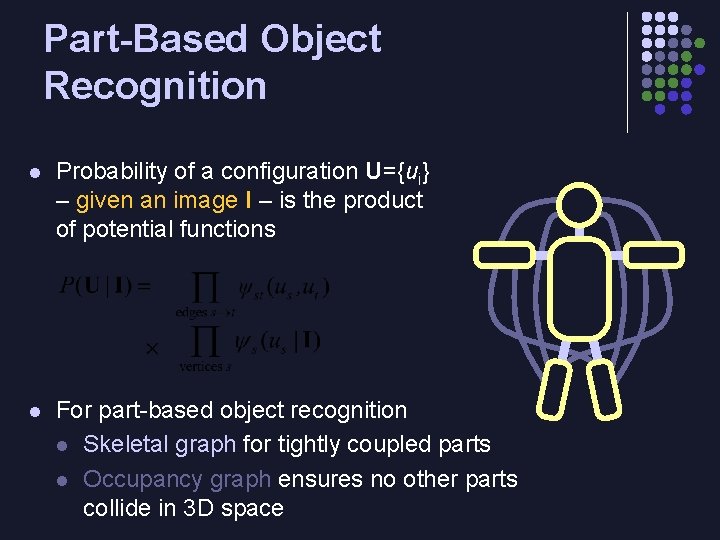
Part-Based Object Recognition l Probability of a configuration U={ui} – given an image I – is the product of potential functions l For part-based object recognition l Skeletal graph for tightly coupled parts l Occupancy graph ensures no other parts collide in 3 D space

Inferring Part Locations with Belief Propagation (BP) l Want to find part configuration maximizing product of potential functions l Use belief propagation (BP) to approximate marginal distributions l Iterative, message-passing method (Pearl 1988) l A message, mi→j, from part i to part j indicates where i currently expects to find j
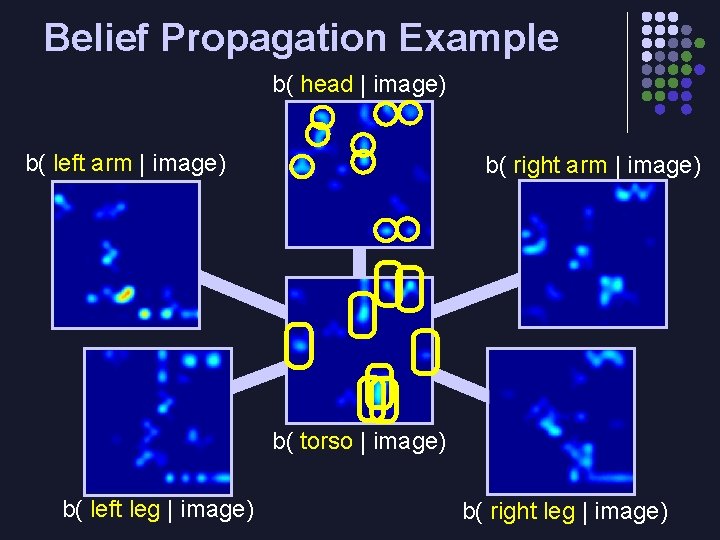
Belief Propagation Example b( head | image) b( left arm | image) b( right arm | image) b( torso | image) b( left leg | image) b( right leg | image)
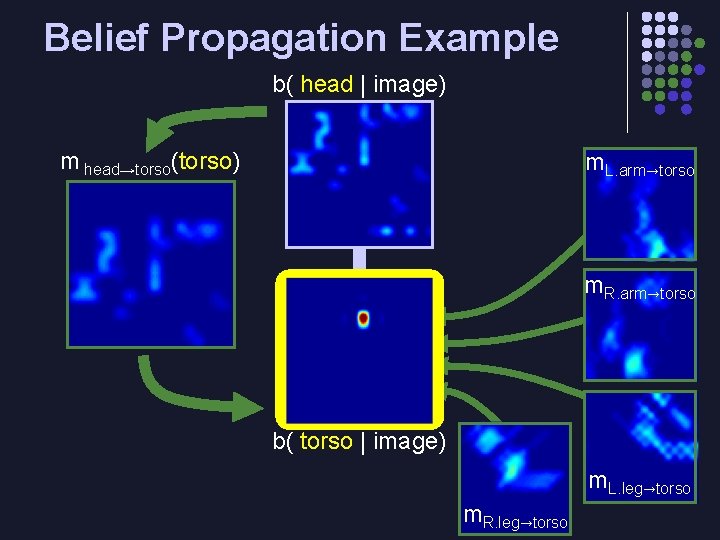
Belief Propagation Example b( head | image) m head→torso(torso) m. L. arm→torso m. R. arm→torso b( torso | image) m. L. leg→torso m. R. leg→torso
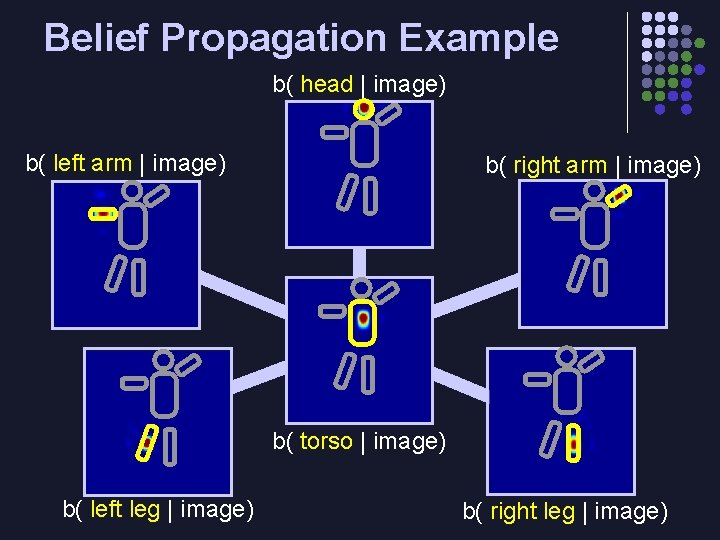
Belief Propagation Example b( head | image) b( left arm | image) b( right arm | image) b( torso | image) b( left leg | image) b( right leg | image)

What if the Graph has Thousands of Parts? l In a graph with N parts and E edges l l l BP running time and memory requirements O(E) Skeleton graph typically sparse – O(N) edges Occupancy graph fully connected – O(N 2) edges l In very large graphs, O(N 2) runtime intractable l Agg. BP (our system) approximates O(N 2) occupancy messages using O(N) messages
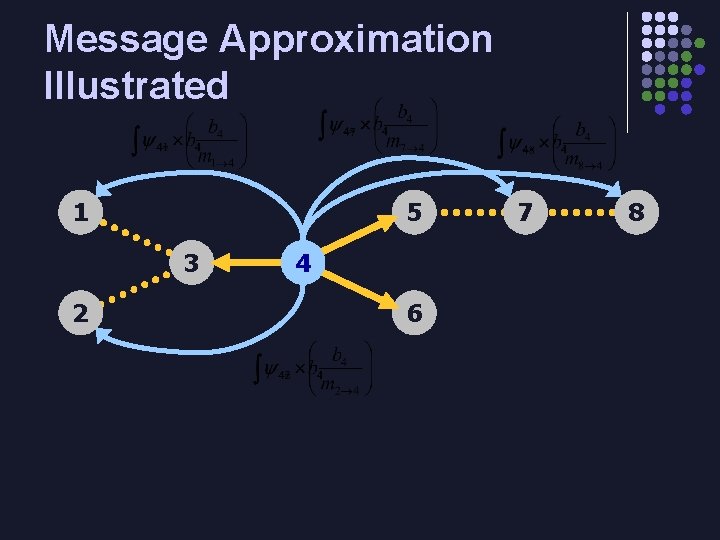
Message Approximation Illustrated 1 5 3 2 4 6 7 8
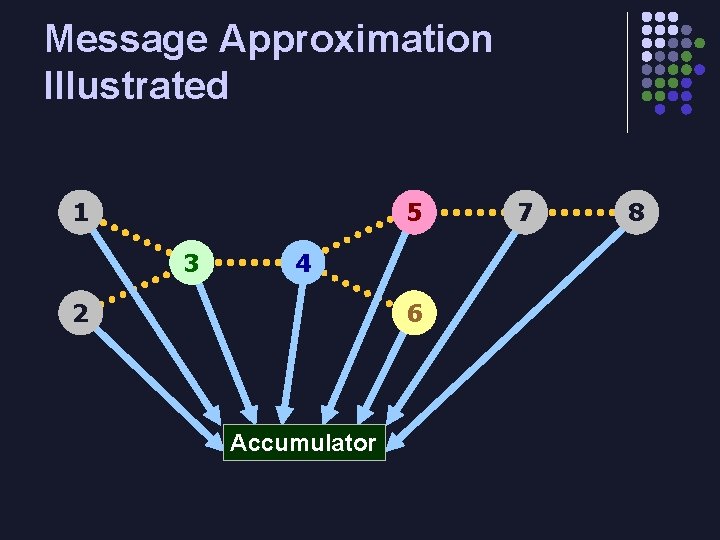
Message Approximation Illustrated 1 5 3 4 2 6 Accumulator 7 8
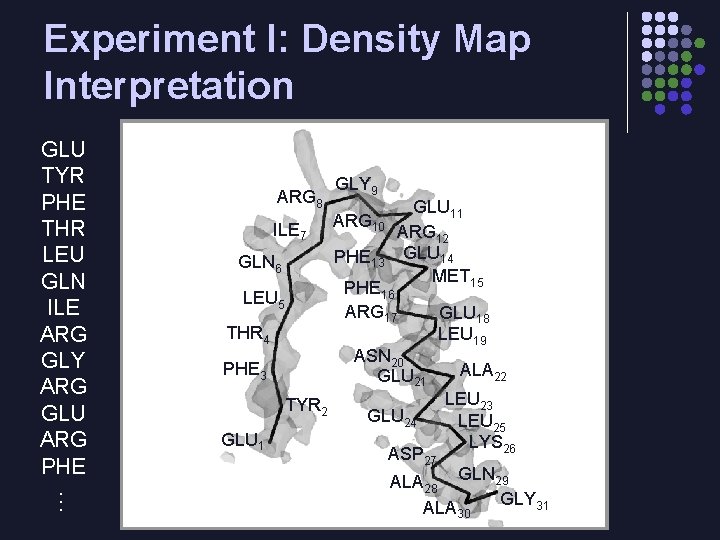
Experiment I: Density Map Interpretation GLU TYR PHE THR LEU GLN ILE ARG GLY ARG GLU ARG PHE ARG 8 ILE 7 ARG 10 PHE 13 GLN 6 GLU 11 ARG 12 GLU 14 MET 15 PHE 16 ARG 17 LEU 5 THR 4 ASN 20 GLU 21 PHE 3 TYR 2 GLU 1 GLY 9 GLU 24 ASP 27 GLU 18 LEU 19 ALA 22 LEU 23 LEU 25 LYS 26 … ALA 28 GLN 29 GLY 31 ALA 30
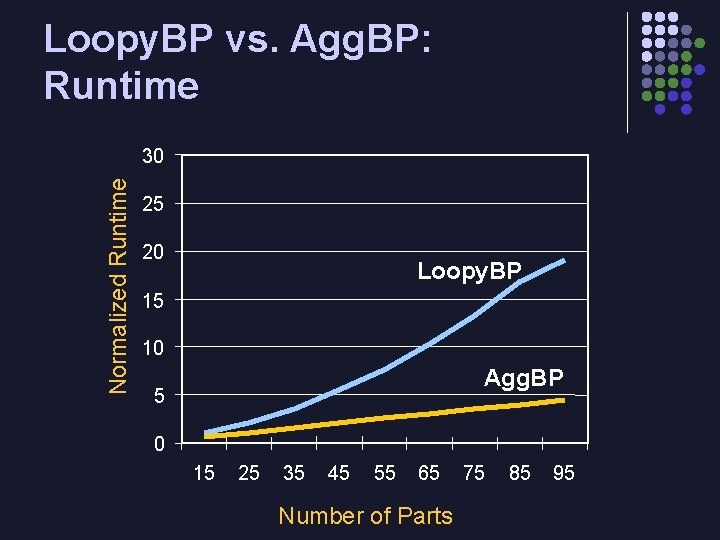
Loopy. BP vs. Agg. BP: Runtime Normalized Runtime 30 25 20 Loopy. BP 15 10 Agg. BP 5 0 15 25 35 45 55 65 Number of Parts 75 85 95
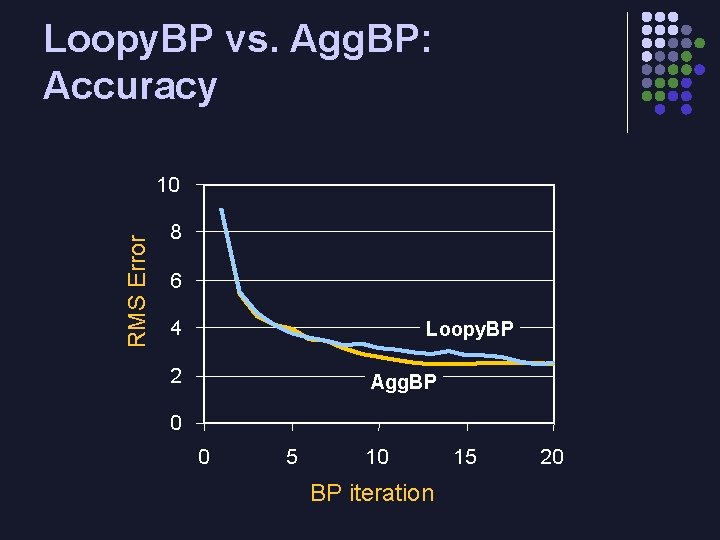
Loopy. BP vs. Agg. BP: Accuracy RMS Error 10 8 6 4 Loopy. BP 2 Agg. BP 0 0 5 10 BP iteration 15 20
![Experiment II: Synthetic Graph Generator increase branching factor allow spatial overlap [skeleton graph] vary Experiment II: Synthetic Graph Generator increase branching factor allow spatial overlap [skeleton graph] vary](http://slidetodoc.com/presentation_image_h2/94c582893618a12225886b26741e0846/image-14.jpg)
Experiment II: Synthetic Graph Generator increase branching factor allow spatial overlap [skeleton graph] vary radii
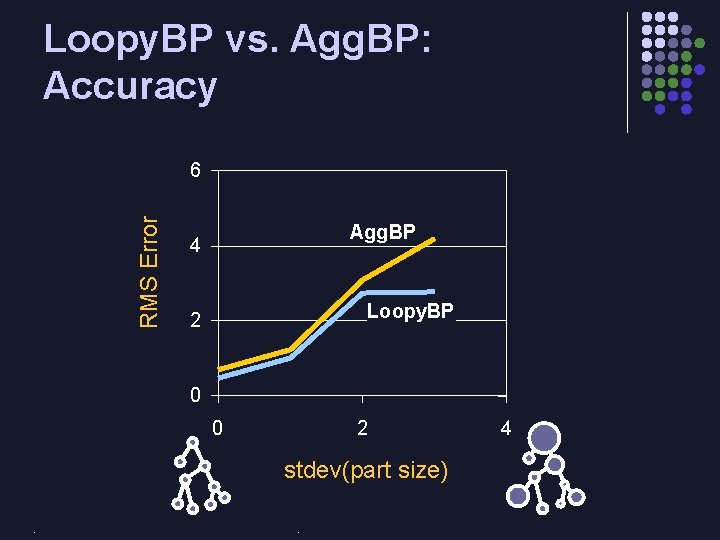
Loopy. BP vs. Agg. BP: Accuracy RMS Error 6 Agg. BP 4 Loopy. BP 2 0 0 2 4 stdev(part size) 0 1 2 5

Conclusions l Agg. BP makes belief propagation tractable in large, highly connected graphs l For part-based modeling, runtime and storage is reduced from O(N 2) to O(N) l Agg. BP’s solutions on two datasets are as good as standard BP’s in less time

Acknowledgements l l l Dr. George Phillips NLM Grant 1 R 01 LM 008796 NLM Grant 1 T 15 LM 007359
- Slides: 17