Belief Nets Notes 6 CDS 1 Bayesian Networks

Belief Nets Notes 6: CDS 1

Bayesian Networks • Closely related ideas – Belief nets – Influence ets • Networks of concepts linked with conditional probabilities • Now easy to calculate for large, moderately complex nets – Connectivity - maximum number of connected nodes – Size - total number of nodes 2
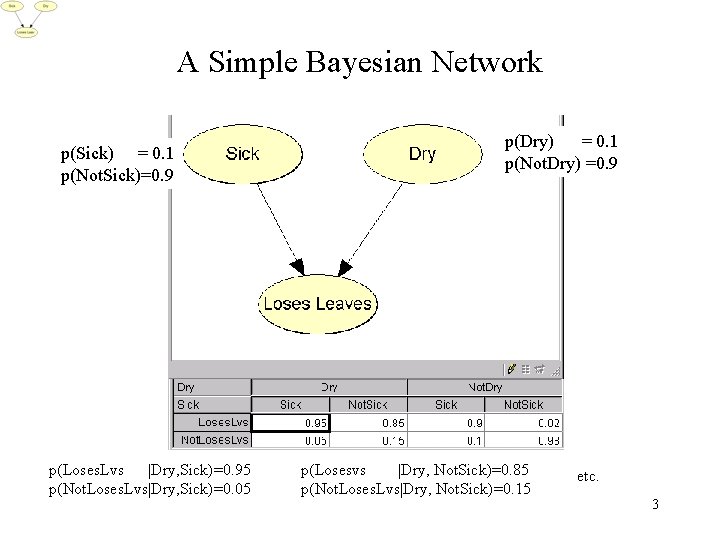
A Simple Bayesian Network p(Sick) = 0. 1 p(Not. Sick)=0. 9 p(Loses. Lvs |Dry, Sick)=0. 95 p(Not. Loses. Lvs|Dry, Sick)=0. 05 p(Dry) = 0. 1 p(Not. Dry) =0. 9 p(Losesvs |Dry, Not. Sick)=0. 85 p(Not. Loses. Lvs|Dry, Not. Sick)=0. 15 etc. 3
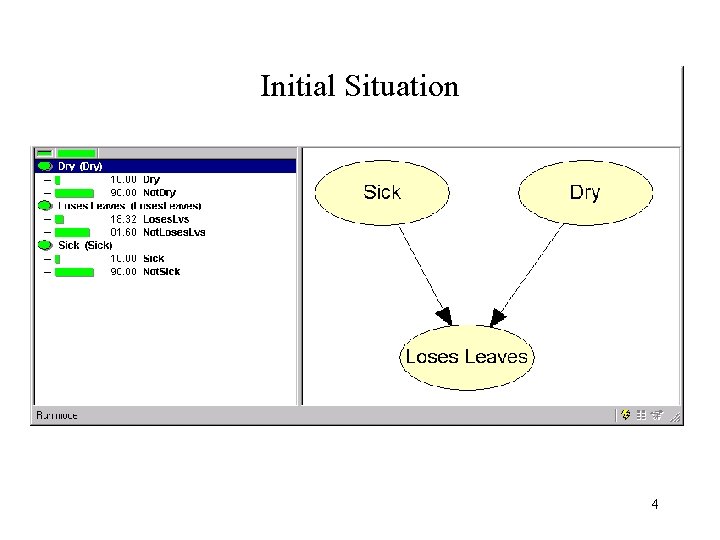
Initial Situation 4
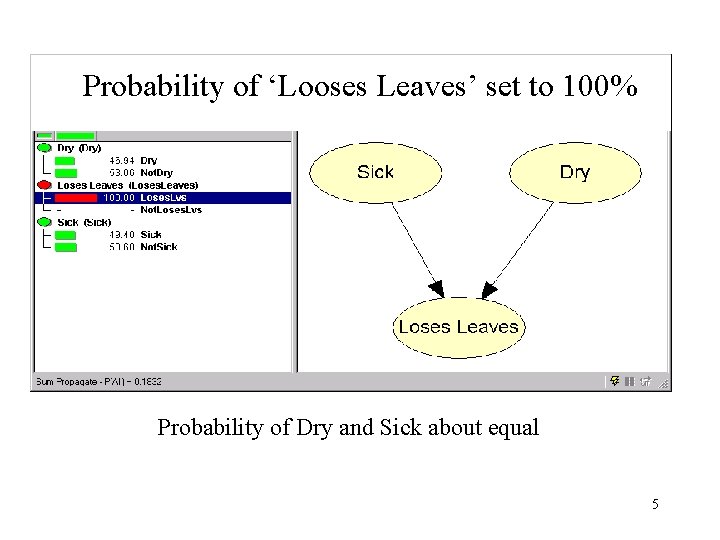
Probability of ‘Looses Leaves’ set to 100% Probability of Dry and Sick about equal 5

Probability of Dry set to 0 Probability of ‘Sick’ now much higher 6
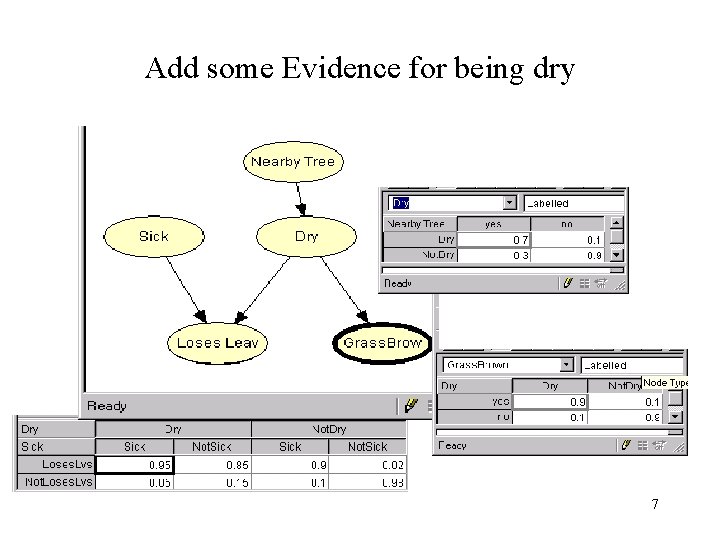
Add some Evidence for being dry 7
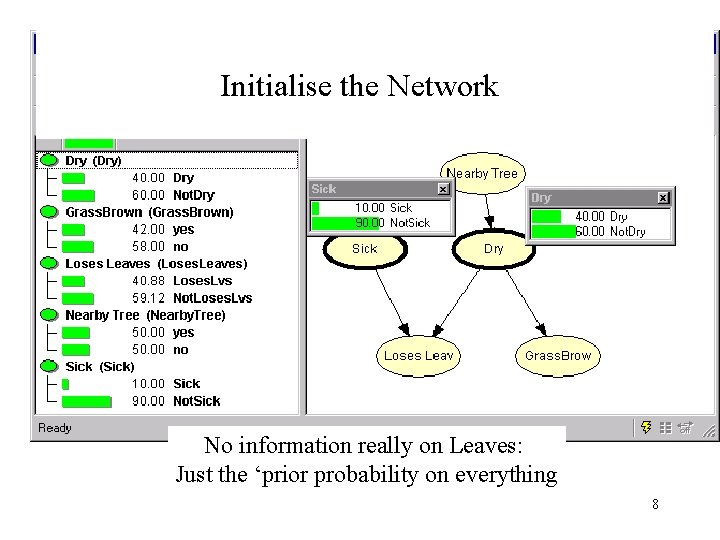
Initialise the Network No information really on Leaves: Just the ‘prior probability on everything 8
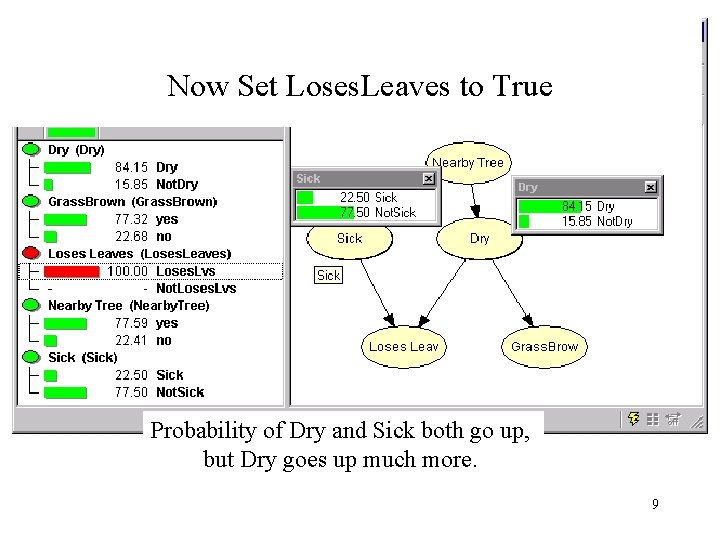
Now Set Loses. Leaves to True Probability of Dry and Sick both go up, but Dry goes up much more. 9
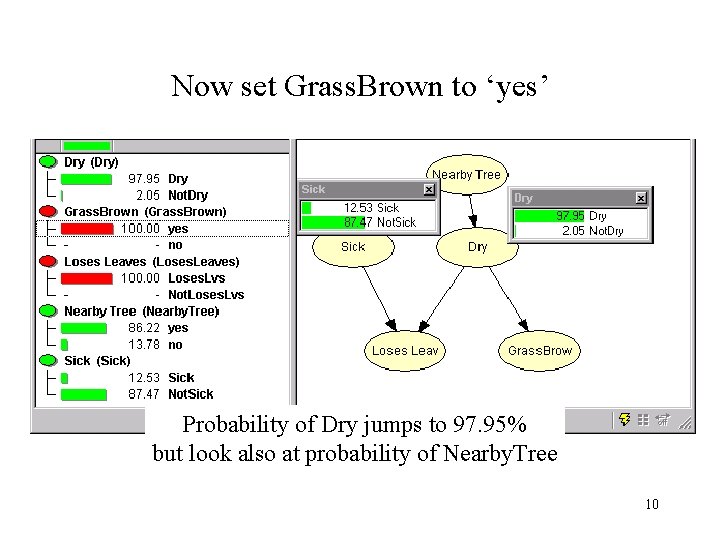
Now set Grass. Brown to ‘yes’ Probability of Dry jumps to 97. 95% but look also at probability of Nearby. Tree 10
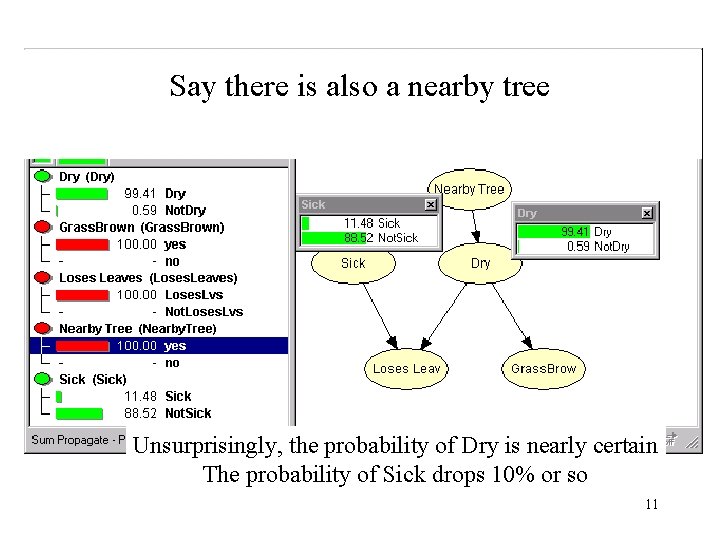
Say there is also a nearby tree Unsurprisingly, the probability of Dry is nearly certain The probability of Sick drops 10% or so 11
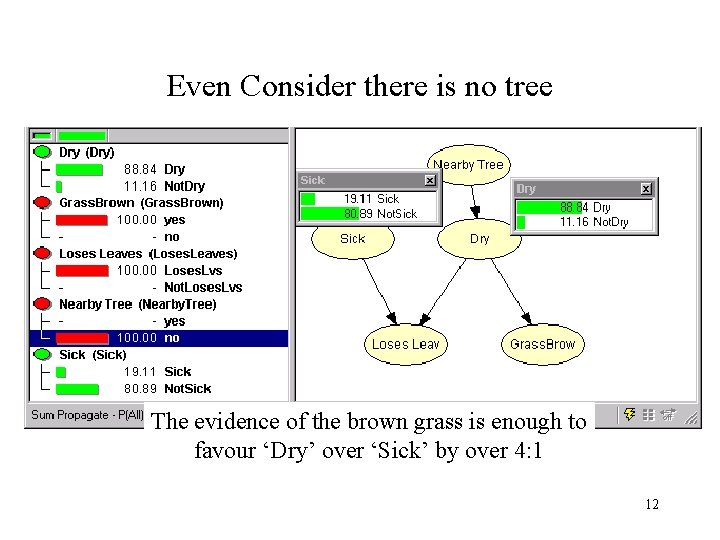
Even Consider there is no tree The evidence of the brown grass is enough to favour ‘Dry’ over ‘Sick’ by over 4: 1 12
Evidence that is ‘Explained away’ is not evidence: consider. . . 13
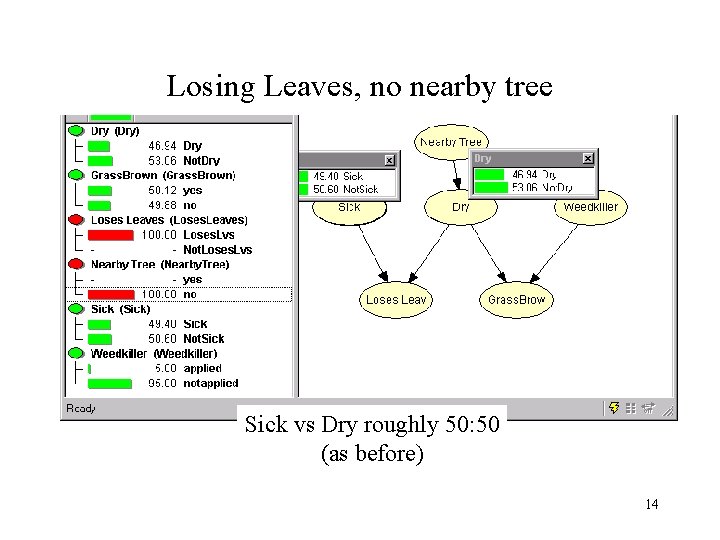
Losing Leaves, no nearby tree Sick vs Dry roughly 50: 50 (as before) 14
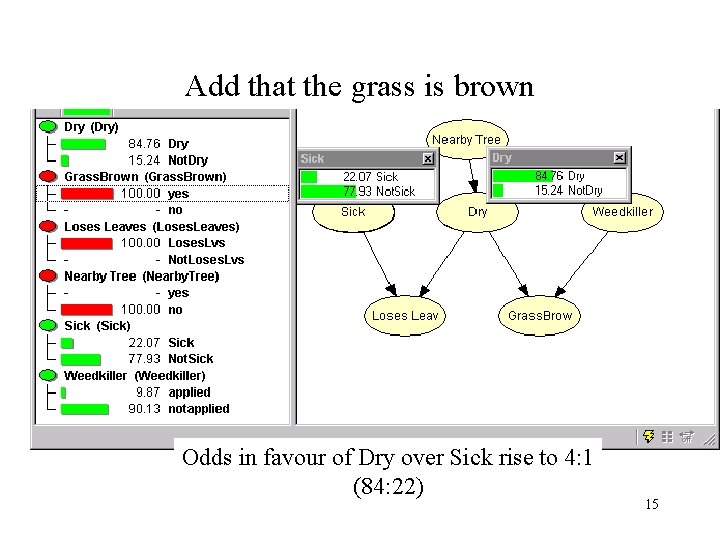
Add that the grass is brown Odds in favour of Dry over Sick rise to 4: 1 (84: 22) 15

Now say that weedkiller was applied The evidence from Grass. Brown is explained away Odds go back to 50: 50 16

Diagnosis from Evidence and Diagnosis by Exclusion • Previous examples were diagnosis from evidence – Normally evidence is a manifestation of the problem • Dryness causes brown grass • Sometimes we also reason from known causes, e. g. Nearby trees can add to dryness • Diagnosis of Exclusion – If there is evidence against all other causes, then the probability of what is left must rise – Consider the next example. . . 17
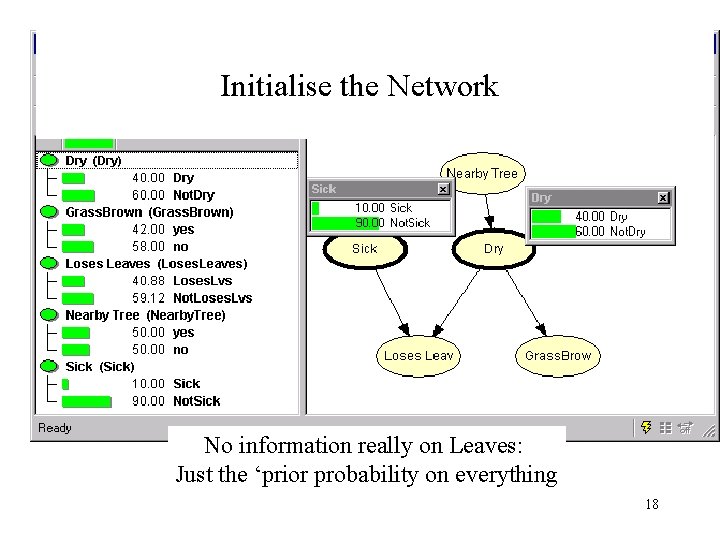
Initialise the Network No information really on Leaves: Just the ‘prior probability on everything 18
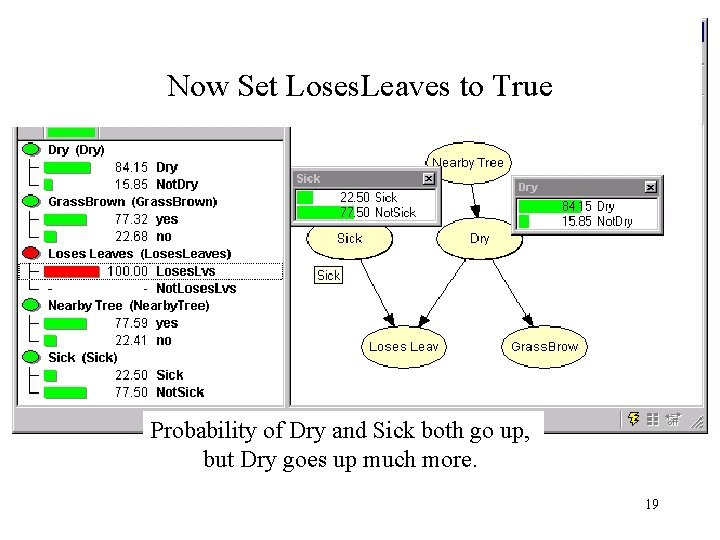
Now Set Loses. Leaves to True Probability of Dry and Sick both go up, but Dry goes up much more. 19
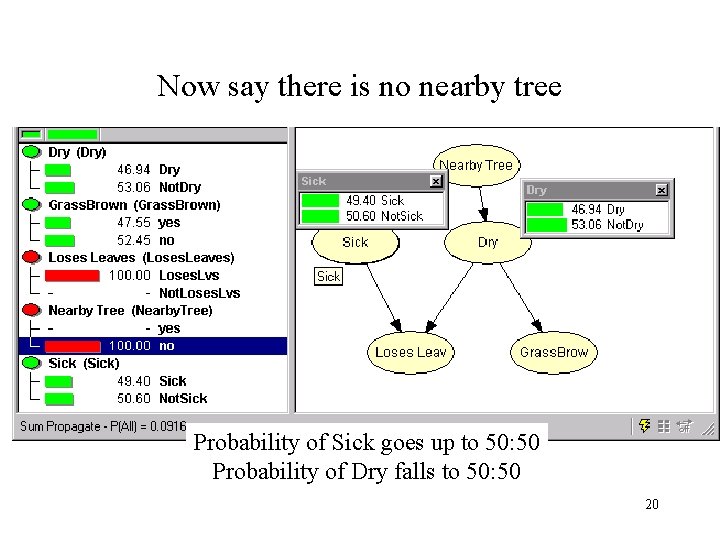
Now say there is no nearby tree Probability of Sick goes up to 50: 50 Probability of Dry falls to 50: 50 20
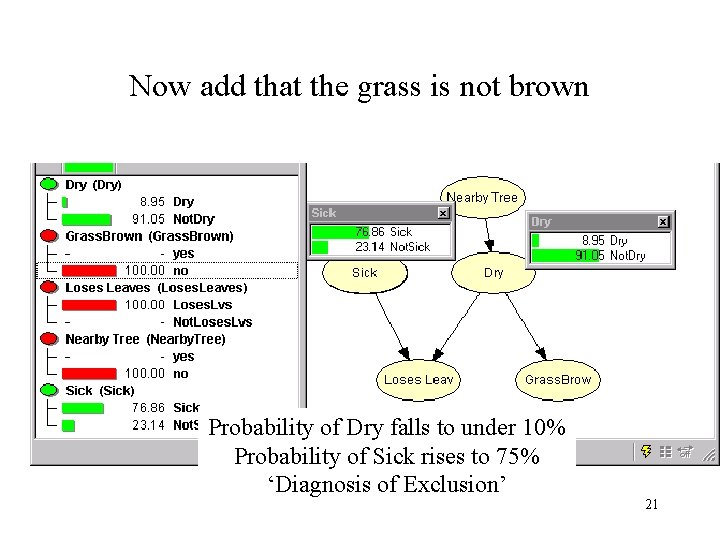
Now add that the grass is not brown Probability of Dry falls to under 10% Probability of Sick rises to 75% ‘Diagnosis of Exclusion’ 21

Bayesian Nets: Summary so far • Probabilities propagate • Probability must go someplace – The good news: Diagnoses of exclusion – The bad news: spurious conclusions 22

IF fungus THEN Black Mould • if P then Q = not both P and not Q – P Q ¬(P & ¬Q) • Equivalent to p(P&¬Q) 0 • If Black Mould then Fungus – There is never black mould without fungus • No fungus implies no black mould 23
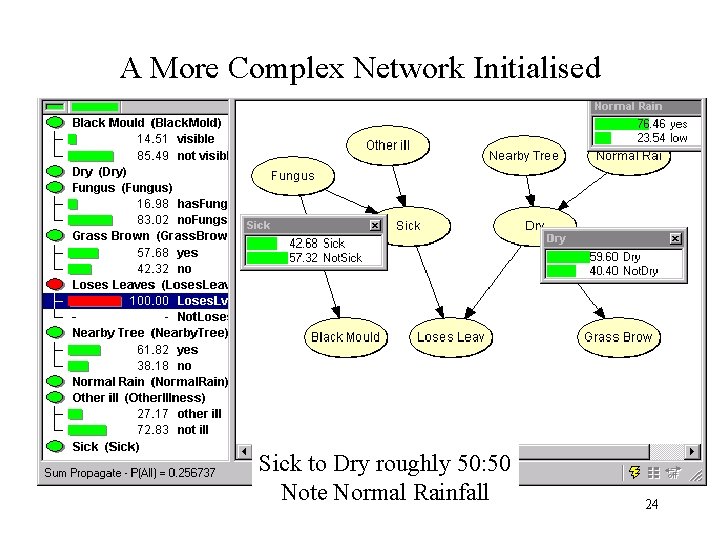
A More Complex Network Initialised Sick to Dry roughly 50: 50 Note Normal Rainfall 24
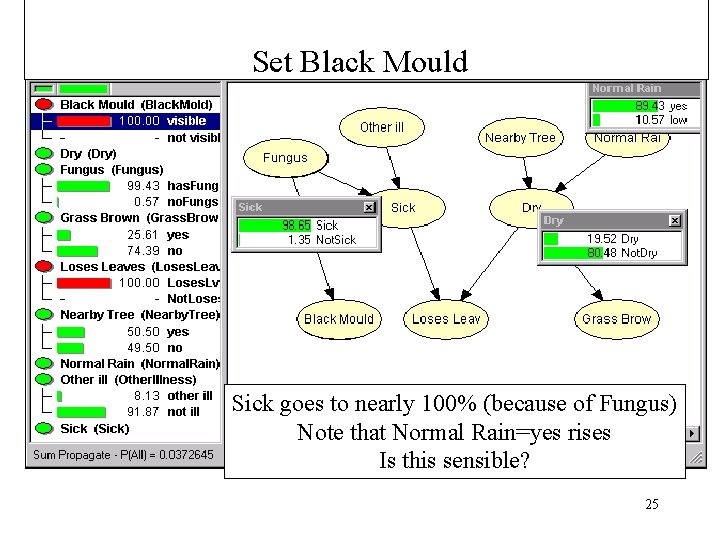
Set Black Mould Sick goes to nearly 100% (because of Fungus) Note that Normal Rain=yes rises Is this sensible? 25
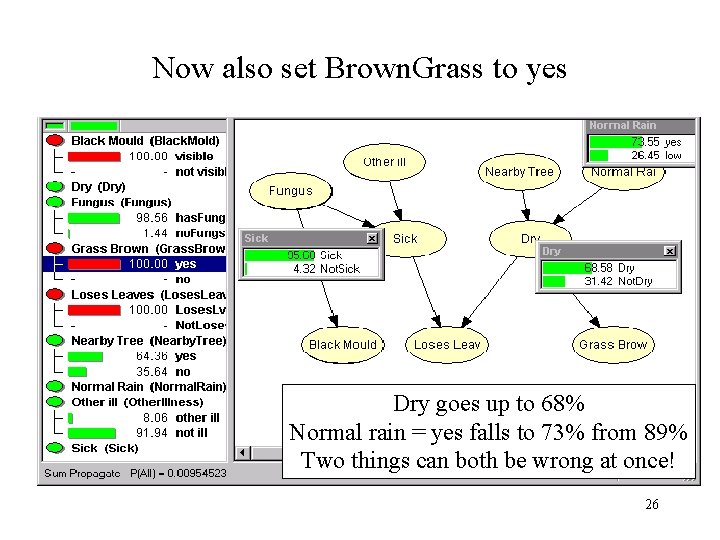
Now also set Brown. Grass to yes Dry goes up to 68% Normal rain = yes falls to 73% from 89% Two things can both be wrong at once! 26
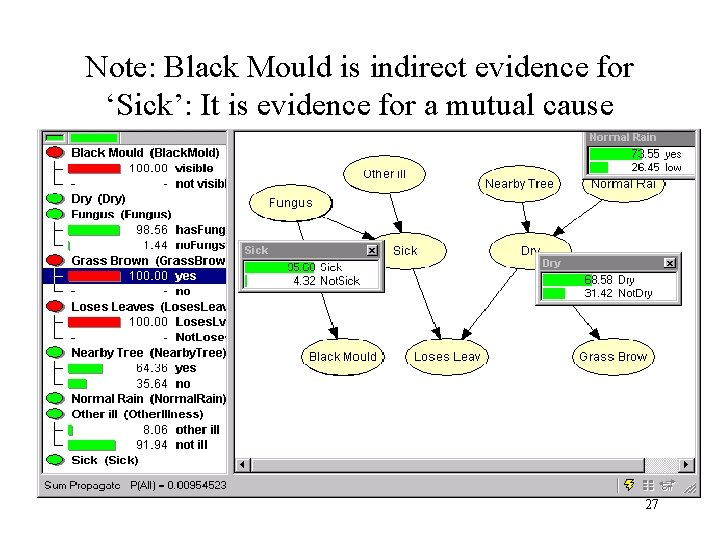
Note: Black Mould is indirect evidence for ‘Sick’: It is evidence for a mutual cause 27

Summary of Bayesian Nets • Formalism is strictly based on probability – Normal practice is to use an ‘influence diagram’ and for arrows in the direction of causation: p(E|H) • Require lots and lots of numbers – But there are many ways of approximating them • Allow reasoning – From cause to effect – From effect to cause – By exclusion • But beware of “residual diagnoses” • P Q shown by negation (probability 0) – equivalences: ¬Q ¬P ¬(P&¬Q) 28

Tools • Several sets of free tools – Hugin-Lite (used for this handout) • www. hugin. com – Excellent tutorials and documentation on Web – Belief net site • http: //bayes. stat. washington. edu/almond/belief. html – Ge. NIe and SMILE • http: //www 2. sis. pitt. edu/~genie – C++ and graphics packages » Good project materal 29
- Slides: 29