Beispiel B Schnitt einer Kugel mit projizierenden Ebenen

Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Ergänzung zum multimedialen, bilingualen (deutsch/englisch) Buch „Darstellende Geometrie/ 3 D-Geometry“ erschienen im Veritas Verlag: Lehrerversion Schülerversion ISBN - 978 -3 -7058 -9079 -4 ISBN - 978 -3 -7058 -9293 -4 Speziell für Lehrende aufbereitetes Werk: Übersichtlich gegliederte Printversion von Theorie und detailliert aufbereiteten Beispielen. Das Kernstück ist die beiliegende CD, mit Theorie und Beispielen in Form von animierten Power. Point. Präsentationen für einfaches und bequemes Lehren geometrischer Inhalte. Speziell für Studierende aufbereitetes Werk: Arbeitsblätter in Printversion mit beiliegender CD. Auf der CD befinden sich Theorie und Beispiele in Form von animierten Power. Point-Präsentationen, die einfaches und bequemes Lernen geometrischer Inhalte bzw. schrittweises Lösen von räumlichen Aufgaben ermöglichen. Für weitere Details und Bestellung 1
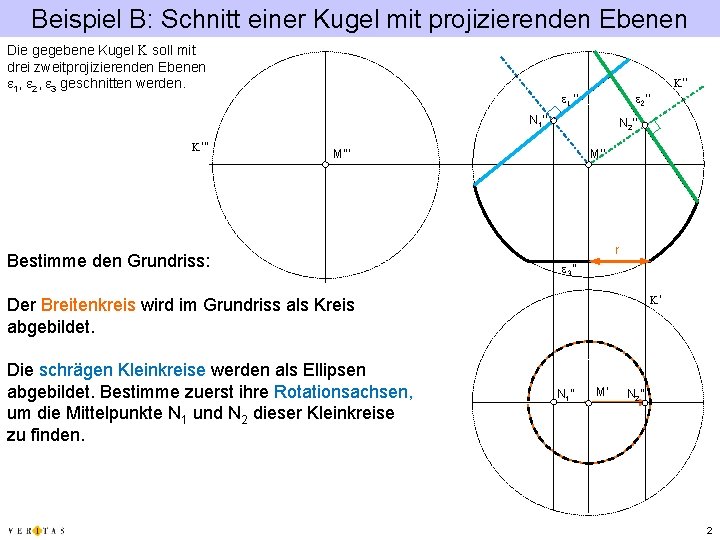
Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Die gegebene Kugel K soll mit drei zweitprojizierenden Ebenen e 1, e 2, e 3 geschnitten werden. K‘‘ e 1 ‘‘ e 2‘‘ N 1’’ K‘‘‘ N 2’’ M’’’ Bestimme den Grundriss: M’’ r e 3‘‘ K‘ Der Breitenkreis wird im Grundriss als Kreis abgebildet. Die schrägen Kleinkreise werden als Ellipsen abgebildet. Bestimme zuerst ihre Rotationsachsen, um die Mittelpunkte N 1 und N 2 dieser Kleinkreise zu finden. N 1’’ M‘ N 2’’ 2

Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Die gegebene Kugel K soll mit drei zweitprojizierenden Ebenen e 1, e 2, e 3 geschnitten werden. 1’’=2’’ e 1 ‘‘ e 2‘‘ N 1’’ K‘‘‘ M’’’ U 1, 2’’ N 2’’ r M’’ r U 3, 4’’ r Bestimme den Grundriss: Bestimme Haupt- und Nebenscheitel der Grundrissellipsen. K‘‘ e 3‘‘ K‘ U 1’ r Ermittle exakt die Schnittpunkte der beiden schrägen Kleinkreise. r N 1’’ Verwende dazu einen Breitenkreis. Ermittle die Umrisspunkte, um die Sichtbarkeit richtig darzustellen. U 3’ 1’ M‘ N 2’’ r r U 2’ 2’ U 4’ 3

Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Die gegebene Kugel K soll mit drei zweitprojizierenden Ebenen e 1, e 2, e 3 geschnitten werden. 1’’=2’’ e 1 ‘‘ e 2‘‘ N 1’’ K‘‘‘ M’’’ U 1, 2’’ N 2’’ r M’’ r U 3, 4’’ r Bestimme den Grundriss: Zeichne die Sichtbarkeit des verbleibenden Kugelteils im Grundriss richtig ein. K‘‘ e 3‘‘ K‘ U 1’ U 3’ 1’ r Konstruiere die Ellipsen mit Hilfe ihrer Scheitelkrümmungskreise. r N 1’’ M‘ N 2’’ r r U 1’ 2’ U 4’ 4
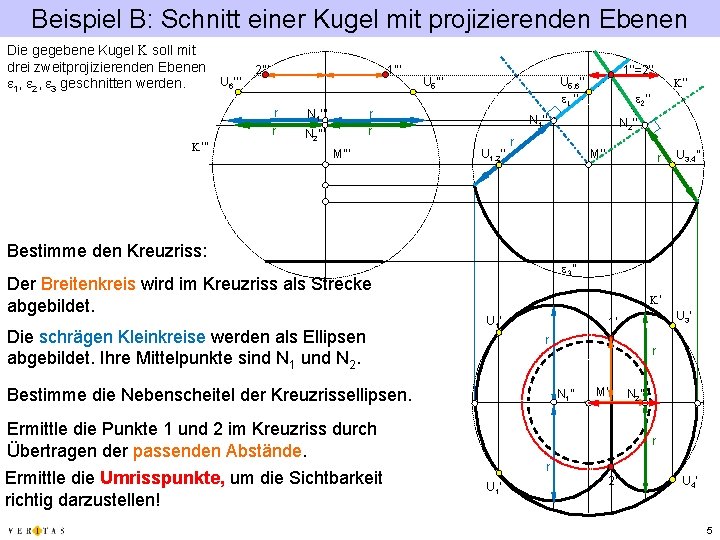
Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Die gegebene Kugel K soll mit drei zweitprojizierenden Ebenen e 1, e 2, e 3 geschnitten werden. K‘‘‘ U 6’’’ 2’’’ 1’’’ r N 2’’’ U 5’’’ r r M’’’ U 1, 2’’ Die schrägen Kleinkreise werden als Ellipsen abgebildet. Ihre Mittelpunkte sind N 1 und N 2’’ r M’’ r U 3, 4’’ e 3‘‘ K‘ U 1’ U 3’ 1’ r Bestimme die Nebenscheitel der Kreuzrissellipsen. r N 1’’ Ermittle die Punkte 1 und 2 im Kreuzriss durch Übertragen der passenden Abstände. Ermittle die Umrisspunkte, um die Sichtbarkeit richtig darzustellen! K‘‘ e 2‘‘ N 1’’ Bestimme den Kreuzriss: Der Breitenkreis wird im Kreuzriss als Strecke abgebildet. 1’’=2’’ U 5, 6’’ e 1 ‘‘ M‘ N 2’’ r r U 1’ 2’ U 4’ 5

Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Die gegebene Kugel K soll mit drei zweitprojizierenden Ebenen e 1, e 2, e 3 geschnitten werden. K‘‘‘ U 6’’’ 2’’’ 1’’’ r N 2’’’ U 5’’’ r r M’’’ 1’’=2’’ U 5, 6’’ e 1 ‘‘ e 2‘‘ N 1’’ U 1, 2’’ N 2’’ r M’’ Bestimme den Kreuzriss: K‘‘ r U 3, 4’’ e 3‘‘ K‘ Zeichne die Sichtbarkeit des verbleibenden Kugelteils im Kreuzriss richtig ein. U 1’ U 3’ 1’ r r N 1’’ Konstruiere die Ellipsen mit Hilfe ihrer Scheitelkrümmungskreise. M‘ N 2’’ r r U 1’ 2’ U 4’ 6
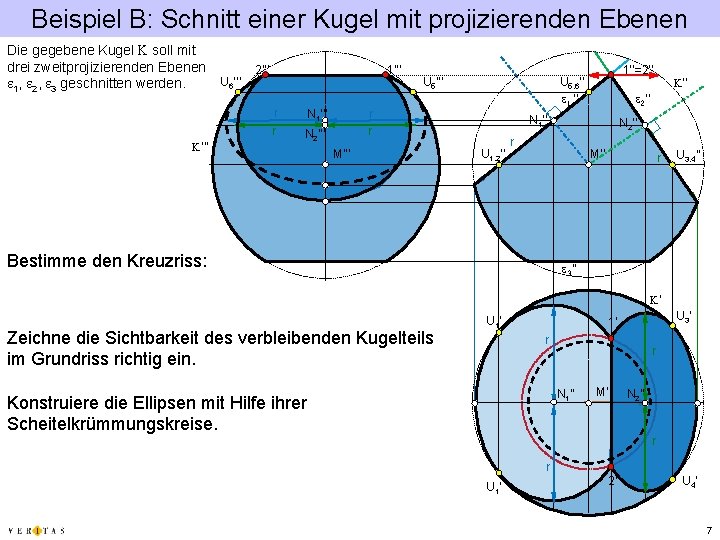
Beispiel B: Schnitt einer Kugel mit projizierenden Ebenen Die gegebene Kugel K soll mit drei zweitprojizierenden Ebenen e 1, e 2, e 3 geschnitten werden. K‘‘‘ U 6’’’ 2’’’ 1’’’ r N 2’’’ U 5’’’ r r M’’’ 1’’=2’’ U 5, 6’’ e 1 ‘‘ e 2‘‘ N 1’’ U 1, 2’’ N 2’’ r M’’ Bestimme den Kreuzriss: K‘‘ r U 3, 4’’ e 3‘‘ K‘ Zeichne die Sichtbarkeit des verbleibenden Kugelteils im Grundriss richtig ein. U 1’ U 3’ 1’ r r N 1’’ Konstruiere die Ellipsen mit Hilfe ihrer Scheitelkrümmungskreise. M‘ N 2’’ r r U 1’ 2’ U 4’ 7
- Slides: 7