Beginning Algebra Dividing a Polynomial by a Monomial

Dividing Polynomials: What to Do 1. Divide a binomial by a monomial How to Do It 9 x 4 12 x 3 3 x 2 using the definition of division, division 1 = (9 x 4 x 3) 3 x 2 the distributive property = 9 x 4 12 x 3 3 x 2 the laws of the exponents = 3 x 2 4 x

Dividing Polynomials: What to Do 2. Divide 6 a 5 15 a 7 by - 3 a using the definition of division, division How to Do It 6 a 5 15 a 7 - 3 a (6 a 5 15 a 7) -1 3 a the distributive property 7 5 15 a 6 a + 3 a 3 a the laws of the exponents - 2 a 4 + 5 a 6

Dividing Polynomials: What to Do 3. Divide a polynomial by a monomial in the same way, watching signs and powers. How to Do It 24 x 5 y 7 18 x 4 y 4 + 3 x 3 y 2 - 6 x 2 y 2 24 x 5 y 7 18 x 4 y 4 3 x 3 y 2 Divide each term using + the distributive property - 6 x 2 y 2 Reduce each fraction to lowest terms: terms 4 x 3 y 5 + 3 x 2 y 2 x 2

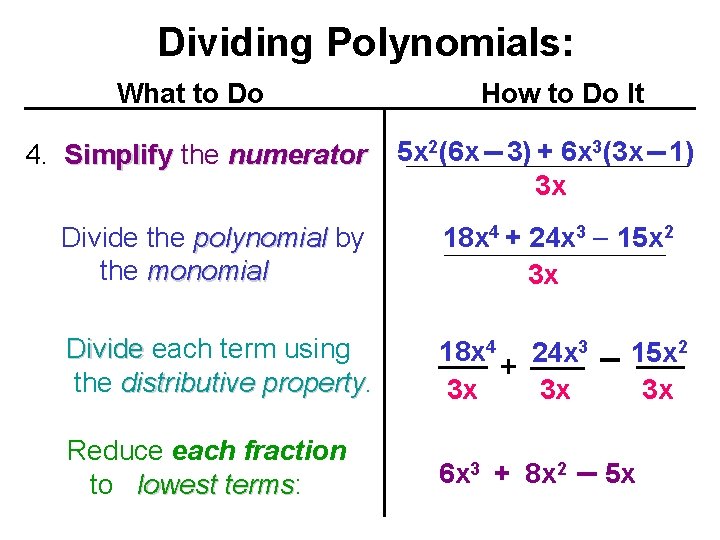
Dividing Polynomials: What to Do 4. Simplify the numerator How to Do It 5 x 2(6 x 3) + 6 x 3(3 x 1) 3 x Divide the polynomial by the monomial 18 x 4 + 24 x 3 15 x 2 3 x Divide each term using the distributive property 18 x 4 24 x 3 + 3 x 3 x Reduce each fraction to lowest terms: terms 6 x 3 + 8 x 2 15 x 2 3 x 5 x

Dividing Polynomials: 5. Show that x + 5 5 by replacing x with 7. x What to Do x+5 5 x when x = 7 How to Do It 7+ 5 5 7 12 5 7 Note: You cannot cancel a piece of a sum

THE END