Beginning Algebra 5 6 Factoring A General Review

Beginning Algebra 5. 6 Factoring: A General Review

6. 5 Factoring: A General Review Objective 1. To factor a variety of polynomials.

6. 5 Factoring: A General Review 1. Check for common factors and factor them out of the polynomial. 2. If there is no common factor check for the two special types of factorable polynomials: . polynomials a) Difference of Squares (binomial). binomial b) Perfect Square Trinomial 3. Check for factors of general polynomial

Factor Common Factors: Polynomials What to do Given a general polynomial: polynomial How to do it 25 ax 3 - 40 abx 2 + 15 a 2 x 2 Check for common factors and factor them out of the polynomial. 5 ax 2(5 x - 8 b + 3 a) Given a general binomial: binomial 64 a 2 x 2 + 16 b 2 x 2 Check for common factors and factor them out of the polynomial. 16 x 2(4 a 2 + b 2) prime factor

Factor general polynomials: What to do Given a special binomial Check for common factors and factor them out of the polynomial. Rewrite square factor( factor s) in the inner binomial Factor as sum and difference of bases of the squares Multiply by common factor 16 x 2 How to do it 64 a 2 x 2 – 16 b 2 x 2 16 x 2(4 a 2 – b 2) difference of squares (2 a)2 – (b)2 difference of squares (2 a + b)(2 a – b) prime factors 64 a 2 x 2 – 16 b 2 x 2 = 16 x 2(2 a + b)(2 a – b)

Factor Difference of Squares: Squares What to Do Given Even Degree Binomial: Binomial Rewrite square factor( factor s) in each term. Factor as sum and difference of bases of the squares The factors of difference of squares form the product of conjugate pairs How to Do It a 2 b 2 – 9 c 2 (ab)2 – (3 c)2 difference of squares (ab + 3 c)(ab – 3 c) prime factors a 2 b 2 – 9 c 2 = (ab + 3 c)(ab – 3 c)

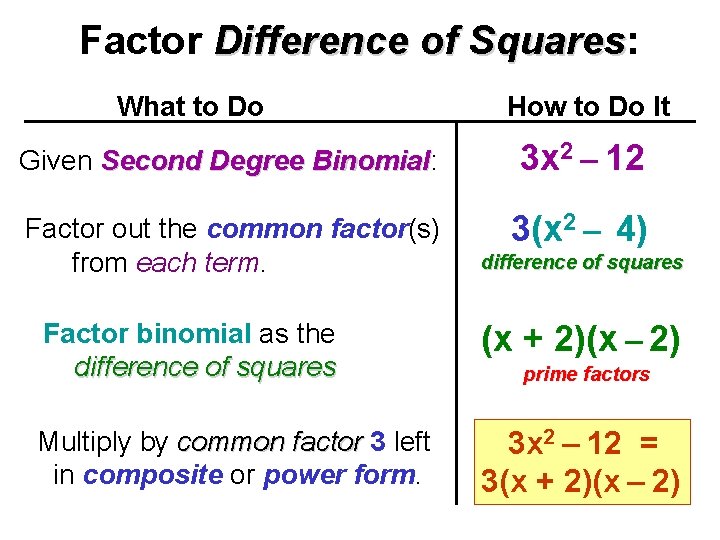
Factor Difference of Squares: Squares What to Do How to Do It Given Second Degree Binomial: Binomial 3 x 2 – 12 Factor out the common factor(s) from each term. 3(x 2 – 4) difference of squares Factor binomial as the difference of squares (x + 2)(x – 2) Multiply by common factor 3 left in composite or power form. 3 x 2 – 12 = 3(x + 2)(x – 2) prime factors

Factor Difference of Squares: Squares What to Do How to Do It Given Even Degree Binomial: Binomial x 4 – y 8 Rewrite square factor( factor s) in each term. (x 2)2 – (y 4)2 Factor as sum and difference of bases of the squares difference of squares (x 2 + y 4)(x x 2 – y 4 ) difference of squares 2 + y 4)(x + y 2)(x – y 2) (x Factor second binomial again. prime factors Completely factor the difference of squares requires repeated factoring x 4 – y 8 = (x 2 + y 4)(x + y 2)(x – y 2)

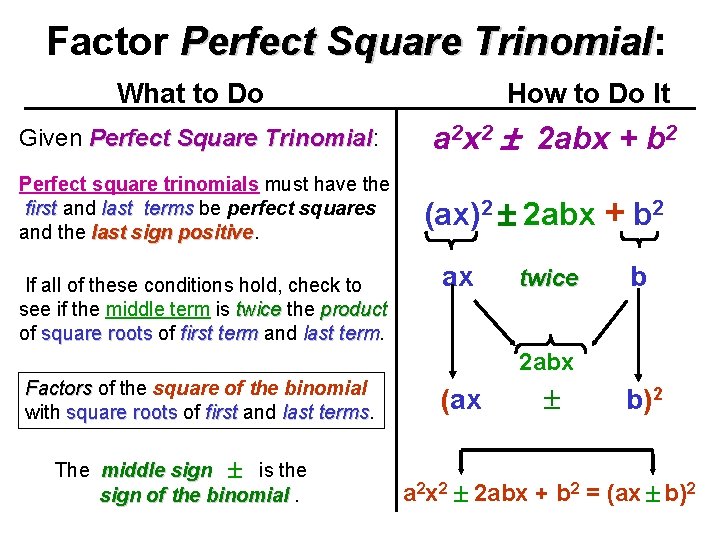
Factor Perfect Square Trinomial: Trinomial What to Do Given Perfect Square Trinomial: Trinomial Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term How to Do It a 2 x 2 2 abx + b 2 (ax)2 2 abx + b 2 ax twice b 2 abx Factors of the square of the binomial with square roots of first and last terms The middle sign is the sign of the binomial. (ax b)2 a 2 x 2 2 abx + b 2 = (ax b)2

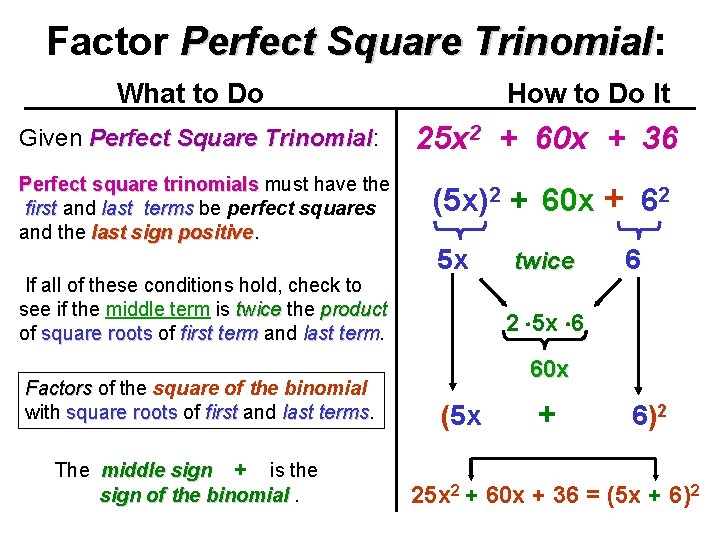
Factor Perfect Square Trinomial: Trinomial What to Do How to Do It Given Perfect Square Trinomial: Trinomial 25 x 2 + 60 x + 36 Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive (5 x)2 + 60 x + 62 If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term Factors of the square of the binomial with square roots of first and last terms The middle sign + is the sign of the binomial. 5 x twice 6 2 5 x 6 60 x (5 x + 6)2 25 x 2 + 60 x + 36 = (5 x + 6)2

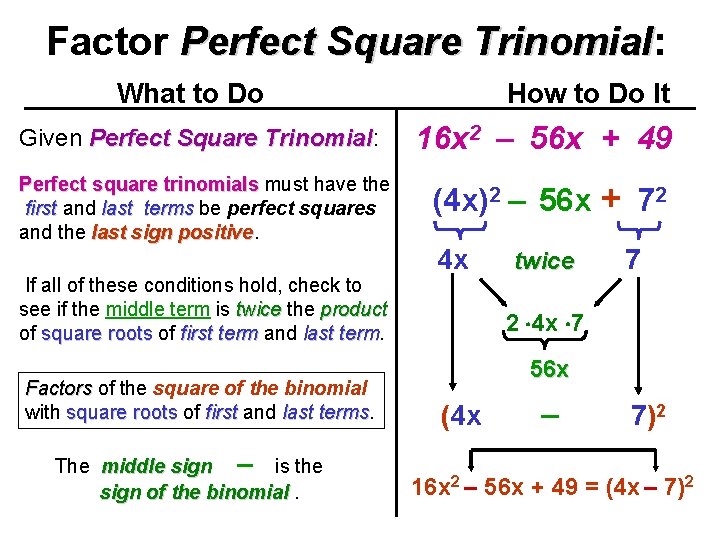
Factor Perfect Square Trinomial: Trinomial What to Do How to Do It Given Perfect Square Trinomial: Trinomial 16 x 2 – 56 x + 49 Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive (4 x)2 – 56 x + 72 If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term Factors of the square of the binomial with square roots of first and last terms The middle sign – is the sign of the binomial. 4 x twice 7 2 4 x 7 56 x (4 x – 7)2 16 x 2 – 56 x + 49 = (4 x – 7)2

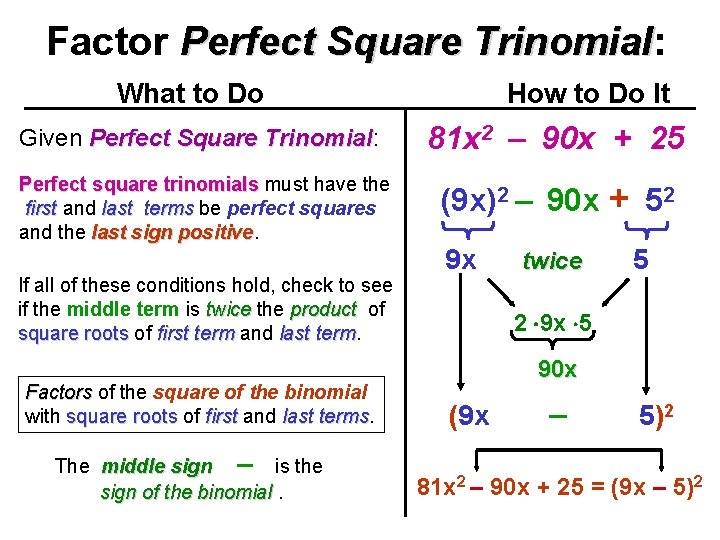
Factor Perfect Square Trinomial: Trinomial What to Do How to Do It Given Perfect Square Trinomial: Trinomial 81 x 2 – 90 x + 25 Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive (9 x)2 – 90 x + 52 If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term Factors of the square of the binomial with square roots of first and last terms The middle sign – is the sign of the binomial. 9 x twice 5 2 9 x 5 90 x (9 x – 5)2 81 x 2 – 90 x + 25 = (9 x – 5)2

Factor general quadratic trinomial: What to do Given a general quadratic trinomial: trinomial How to do it Ax 2 Bx C Find the product of the first and last coefficients: coefficients A and C A C = P Find all of the pairs of factors r and s P = r s, r > s so their sum or difference is the middle coefficient. or r+s=B r–s = B

Factor by Clue of Signs: Signs What to Do How to Do It Given general trinomial that has no common factor. See clues of the signs P = A A C is the grouping number Find all possible factors of GN = P whose sum or difference is B Bx: underline and factor by grouping Sum Ax 2 C Bx + Larger sign Read as “+ or ” Rewrite middle term Same sign Difference P = r s , r > s + sum (r + s) = B – difference (r – s) = B Ax 2 rx sx + C (ax b)(cx d)

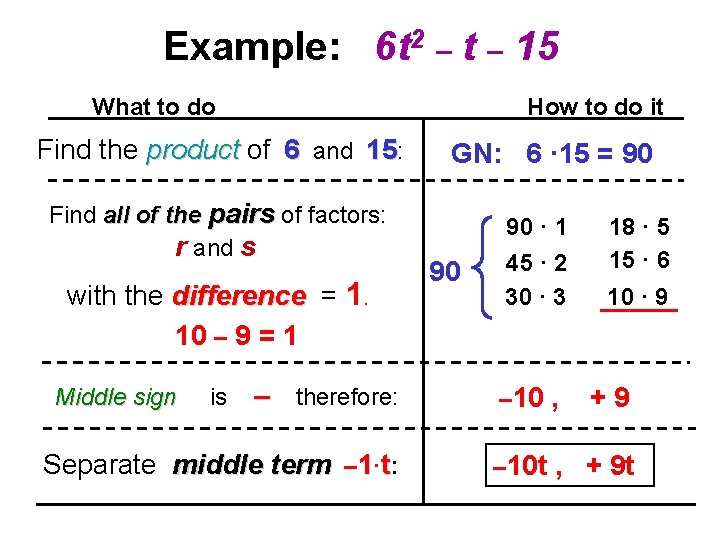
Example: 6 t 2 – t – 15 What to do How to do it Find the product of 6 and 15: Find all of the pairs of factors: r and s with the difference = 1. 10 – 9 = 1 Middle sign is – therefore: Separate middle term – 1·t: GN: 6 · 15 = 90 90 · 1 90 45 · 2 30 · 3 – 10 , 18 · 5 15 · 6 10 · 9 +9 – 10 t , + 9 t

Continue Example: What to do Copy the polynomial: polynomial 6 t 2 – t – 15 How to do it 6 t 2 – t – 15 Rewrite middle term – t: and group for factoring 6 t 2 – 10 t + 9 t – 15 Factor each group: group bring down middle sign 2 t(3 t – 5) + 3(3 t – 5) underline common factor: Factor common factor Always Check Factors. (2 t + 3)(3 t – 5) See next slide:

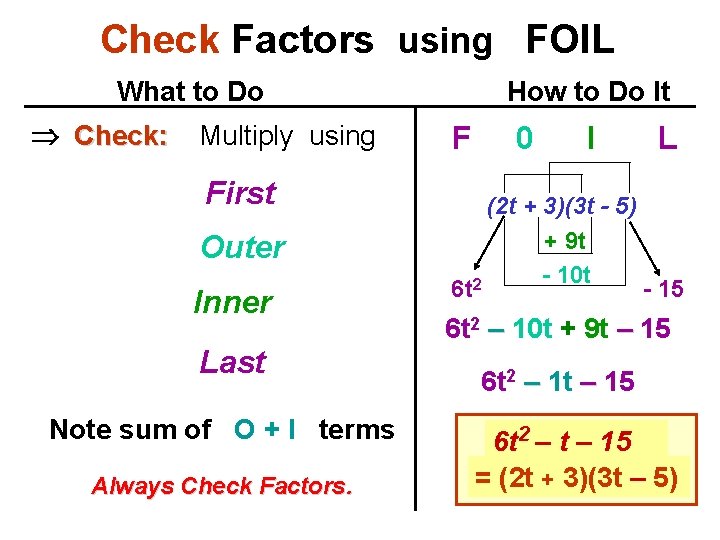
Check Factors using FOIL What to Do Check: Multiply using How to Do It F First Outer Inner Last Note sum of O + I terms Always Check Factors. 6 t 0 I (2 t + 3)(3 t - 5) + 9 t - 10 t 2 L - 15 6 t 2 – 10 t + 9 t – 15 6 t 2 – 1 t – 15 6 t 2 – t – 15 = (2 t + 3)(3 t – 5)

Trinomials with Common Factors: Factors Ax 2 Bx C What to Do How to Do It Factor out the common factor(s) from each term k·ax 2 k·bx k·c Apply the distributive property k·(ax 2 bx c) As common factors numbers are left in composite form and letters are left in power form ax 2 bx c Check Inner Polynomial for Clue of Signs and GN

Trinomials with Common Factors: Factors 72 x 2 – 60 x – 28 What to Do How to Do It Factor out the common factor(s) from each term. 4· 18 x 2 – 4· 15 x – 4· 7 Apply the distributive property 4(18 x 2 – 15 x – 7) Numbers as common factors are left in composite form Hold the 4 Check: Inner Polynomial for Clue of Signs and GN 18 x 2 – 15 x – 7

2 - 15 x - 7 Inner Trinomial: 18 x Trinomial What to do How to do it Find the product of 18 and 7: 18 · 7 = 126 Find all of the pairs of factors: r and s 126 · 1 with the difference = 15. 126 63 · 2 42 · 3 21 · 6 18 · 7 14 · 9 21 - 6 = 15 Middle sign is – therefore: Separate middle term - 15 x: - 21 , + 6 - 21 x , + 6 x

Continue Example: What to do Copy the polynomial: polynomial Rewrite middle term -15 x : and group for factoring Factor each group: group bring down middle sign 18 x 2 – 15 x – 7 How to do it 18 x 2 – 15 x – 7 18 x 2 – 21 x + 6 x – 7 3 x(6 x - 7) ++ 1(6 x - 7) underline common factor: Factor common factor Always Check Factors. (3 x + 1)(6 x – 7) See next slide:

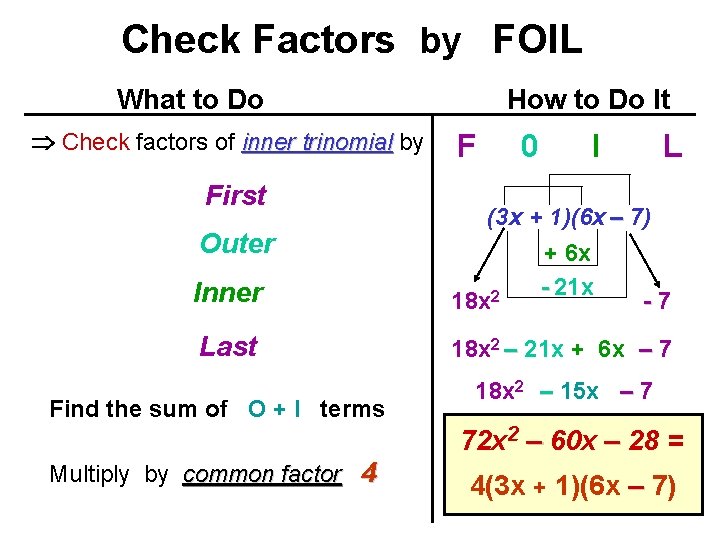
Check Factors by FOIL What to Do Check factors of inner trinomial by First How to Do It F 0 I L Inner (3 x + 1)(6 x – 7) + 6 x - 21 x 2 18 x -7 Last 18 x 2 – 21 x + 6 x – 7 Outer Find the sum of O + I terms Multiply by common factor 4 18 x 2 – 15 x – 7 72 x 2 – 60 x – 28 = 4(3 x + 1)(6 x – 7)

Quadratic Trinomial Test for Factorability: Factorability What to do The test requires knowing squares of integers or use to a calculator. Given a quadratic trinomial and integers a, b, c a>0 How to do it Review squares of integers ax 2 + bx + c signs included in b and c The trinomial will factor with have rational factors b 2 – 4 ac = d 2 if: 0 perfect square trinomial. d 2 factorable trinomial. d 0 d 2 = +d

Quadratic Trinomial Test for Factorability: Factorability What to do Test 4 x 2 – 12 x - 9 a = 4, b = -12, c = -9 Test 4 x 2 – 12 x + 9 How to do it 4 x 2 – 12 x – 9 (-12)2 – 4(4)(-9) = 288 d 2 not factorable 4 x 2 – 12 x + 9 a = 4, b = -12, c = 9 (-12)2 – 4(4)(9) = 0 b 2 – 4 ac = 0 perfect square trinomial Perfect square trinomial yields square of binomial 4 x 2 – 12 x - 9 = (2 a – 3)2

Quadratic Trinomial Test for Factorability: Factorability What to do Test 4 x 2 +15 x + 9 a = 4, b = -15, c = 9 Factor 4 x 2 + 15 x + 9 GN = 36 -- factors 12 and 3 Sum: 12 + 3 = 15 Complete the factors: How to do it 4 x 2 + 15 x + 9 (-15)2 – 4(4)(9) = 81 = 92 factorable trinomial 4 x 2 + 15 x + 9 4 x 2 + 12 x + 3 x + 9 4 x(x + 3) + 3(x + 3) 4 x 2 + 15 x + 9 = (4 x + 3)(x + 3)

Summary: Factor Polynomials What to do How to do it Factor: common factors: factors ax + ay = a(x + y) Distribute: left / right ax + bx = (a + b)x Perfect square trinomial binomial squared a 2 x 2 2 abx + b 2 (ax b)2 Difference of Squares: Squares A 2 – B 2 = (A + B)(A – B) Conjugate Pairs: Pairs a 2 x 2 – b 2 y 2 = (ax+by)(ax – by)

Summary: Factor Polynomials What to do Difference of like even powers Repeat if m = 2 p (xm + ym) is prime n = 4, m = 2: x 4 – y 4 = Repeat since m = 2 (xm + ym) is prime n = 8, m = 4, p = 2: x 8 – y 8 = Repeat since m = 4, p = 2 (xm + ym) is prime How to do it xn - yn = (x 2 m – y 2 m) (xm + ym)(xm – ym) [(x 2)2 – (y 2)2] (x 2 + y 2)(x 2 – y 2) (x 2 + y 2)(x + y)( x – y) (x 4 + y 4)(x 4 – y 4) (x 4+y 4)(x 2+ y 2)(x 2 – y 2) (x 4+y 4)(x 2+ y 2)(x+ y)(x – y)

Summary: Factor Polynomials What to do Factor by grouping ax + by - bx - ay Apply commutative property Underline groups: groups How to do it Polynomials of 4 or more terms rearranged / grouped: grouped = ax – ay – bx + by Apply distributive property: = a(x – y) – b(x – y) Underline common factor: = a(x – y) – b(x – y) Apply distributive property = (a – b)(x – y)

5. 6 THE END