Beginning Algebra 5 4 The Difference of Two

Beginning Algebra 5. 4 The Difference of Two Squares 5. 5 The Sum and Difference of Two Cubes

6. 4 Factoring Trinomials Objective 1. To factor the difference of squares. Objective 2. To factor a perfect square trinomial. Objective 3. To factor a polynomial by first factoring out the greatest common factor and then factoring the polynomial that remains.

Factor Difference of Squares: Some rules for factoring the difference of squares: squares 1. The numbers (coefficients) must be squares 2. The powers must be even whole numbers 3. Binomials that are the sums of squares will be Prime Factors

Factor Difference of Squares: Squares Factorable binomials include: a) The difference of a second degree term with any real square number, number such as: (x 2 – 4), (y 2 – 9), (4 z 2 – 25), (16 – x 2), etc. b) The difference of two even-powered terms (2 or higher) such as: (9 x 2 – 49 y 2), (a 2 b 2 – 9 c 2), (4 z 4 – 16), (x 8 – 81), etc. c) The difference of two even-powered terms (2 or higher) such as: (x 4 – y 4), (x 16 – y 16), (x 2 – y 6), (x 4 – y 8)

Factor Difference of Squares: Squares Prime binomial factors include: a) Linear binomials, binomials such as: (x - 4), (a + b), (9 + y) b) The sum of an even degree term (2 or higher) with any real number, such as: (x 2 + 4), (a 2 b 2 + 9 b 2), (4 z 2 + 25), (x 4 + 16 y 2), etc. c) The sum of two even-powered terms, terms such as: (x 4 + y 4), (x 16 + y 16), (x 2 + y 6), (x 4 + y 8 ), etc. d) Differences that may contain squares, squares such as: (2 x 2 – 3), (a 2 – 5), (a 2 – b 3 ), etc.

Review Multiplication of Conjugates What to Do How to Do It Product of special binomials sum and difference: (4 x + 7)(4 x – 7) The sum and difference of the same two numbers are called conjugate pairs F O I L (4 x + 7)(4 x – 7) 28 x - 27 x Note sum of O + I terms: Product of conjugate pairs: difference of squares. 16 x 2 + 0 – 49 (4 x + 7)(4 x – 7) = 16 x 2 – 49

Review Multiplication of Conjugates What to Do The sum and difference of the same two numbers are called conjugate pairs Product of special binomials sum and difference: How to Do It (2 x + 3)(2 x – 3) + 6 x - 6 x Note sum of O + I terms: Product of conjugate pairs: difference of squares. 4 x 2 + 0 – 9 (2 x + 3)(2 x – 3) = 4 x 2 – 9

Review Multiplication of Conjugates What to Do The sum and difference of the same two numbers are called conjugate pairs Product of special binomials sum and difference: How to Do It (3 x + 5)(3 x – 5) + 15 x - 15 x Note sum of O + I terms: 9 x 2 + 0 – 25 Product of conjugate pairs: (3 x + 5)(3 x – 5) difference of squares. = 9 x 2 – 25

Product of Binomial Conjugates The sum and difference of the same two numbers are called conjugate pairs The product of conjugates is the difference of the square of the first term and square of the last term (A + B)(A – B) = 2 A – 2 B Conjugate Pairs Difference of Squares

Factor Difference of Squares: Squares The sum and difference of the same two numbers are called conjugate pairs The factors of the difference of the squares are the product of conjugates 2 A – 2 B = (A + B)(A – B) Difference of Squares Conjugate Pairs

Factor Difference of Squares: Squares What to do How to do it Given a binomial difference of squares: squares A 2 – B 2 Factor as sum and difference of bases of the squares Given a binomial difference of squares: squares Factor as sum and difference of bases of the squares (A + B)(A – B) 2 2 x –y (x + y)(x – y)
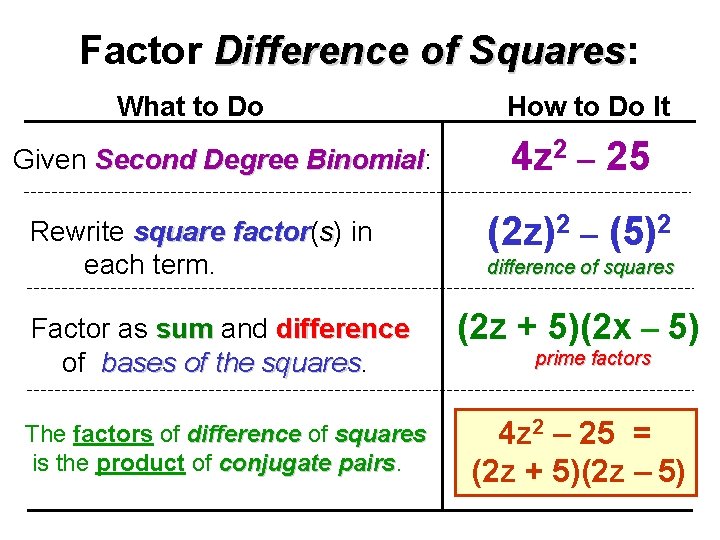
Factor Difference of Squares: Squares What to Do Given Second Degree Binomial: Binomial Rewrite square factor( factor s) in each term. How to Do It 4 z 2 – 25 (2 z)2 – (5)2 difference of squares Factor as sum and difference of bases of the squares (2 z + 5)(2 x – 5) The factors of difference of squares is the product of conjugate pairs 4 z 2 – 25 = (2 z + 5)(2 z – 5) prime factors

Factor Difference of Squares: Squares What to Do Given Second Degree Binomial: Binomial Rewrite square factor( factor s) in each term. Check if necessary. How to Do It y 2 – 289 (y)2 – (17)2 difference of squares Factor as sum and difference of bases of the squares (y + 17)(y – 17) The factors of difference of squares is the product of conjugate pairs y 2 – 289 = (y + 17)(y – 17) prime factors
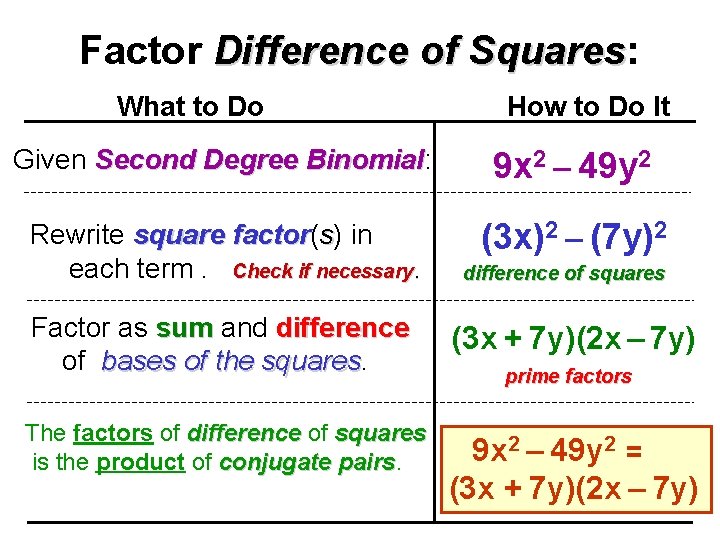
Factor Difference of Squares: Squares What to Do How to Do It Given Second Degree Binomial: Binomial 9 x 2 – 49 y 2 Rewrite square factor( factor s) in each term. Check if necessary. (3 x)2 – (7 y)2 Factor as sum and difference of bases of the squares The factors of difference of squares is the product of conjugate pairs difference of squares (3 x + 7 y)(2 x – 7 y) prime factors 9 x 2 – 49 y 2 = (3 x + 7 y)(2 x – 7 y)
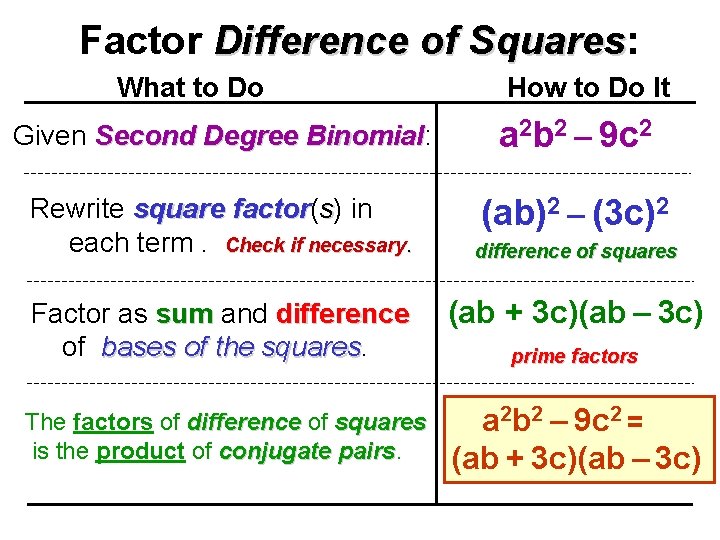
Factor Difference of Squares: Squares What to Do How to Do It Given Second Degree Binomial: Binomial a 2 b 2 – 9 c 2 Rewrite square factor( factor s) in each term. Check if necessary. (ab)2 – (3 c)2 difference of squares Factor as sum and difference of bases of the squares (ab + 3 c)(ab – 3 c) The factors of difference of squares is the product of conjugate pairs a 2 b 2 – 9 c 2 = (ab + 3 c)(ab – 3 c) prime factors
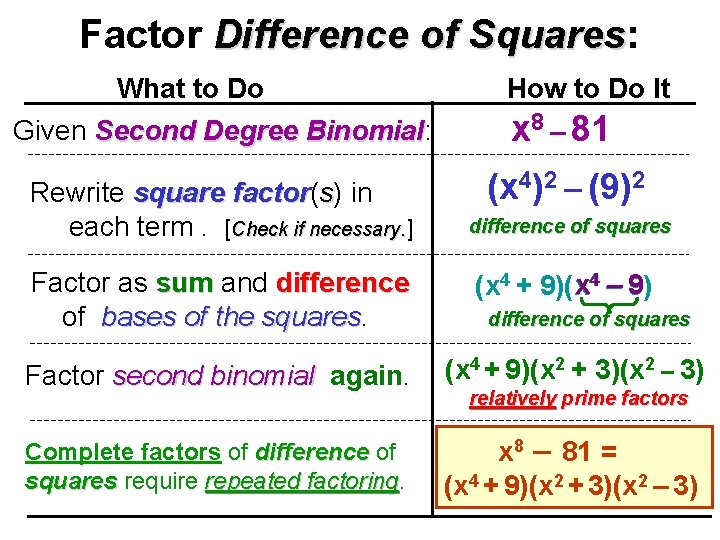
Factor Difference of Squares: Squares What to Do How to Do It Given Second Degree Binomial: Binomial x 8 – 81 Rewrite square factor( factor s) in each term. [Check if necessary. ] (x 4)2 – (9)2 Factor as sum and difference of bases of the squares difference of squares x 4 – 9) 9 (x 4 + 9)(x difference of squares Factor second binomial again. (x 4 + 9)(x 2 + 3)(x 2 – 3) Complete factors of difference of squares require repeated factoring x 8 – 81 = (x 4 + 9)(x 2 + 3)(x 2 – 3) relatively prime factors

Factor Difference of Squares: Squares What to Do Given Second Degree Binomial: Binomial Rewrite square factor( factor s) in each term. Check if necessary. Factor as sum and difference of bases of the squares Factor second binomial again. Complete factors of difference of squares require repeated factoring How to Do It x 4 – y 8 (x 2)2 – (y 4)2 difference of squares x 2 – y 4) (x 2 + y 4)(x difference of squares (x 2 + y 4)(x + y 2)(x – y 2) relatively prime factors x 4 – y 8 = (x 2 + y 4)(x + y 2)(x – y 2)
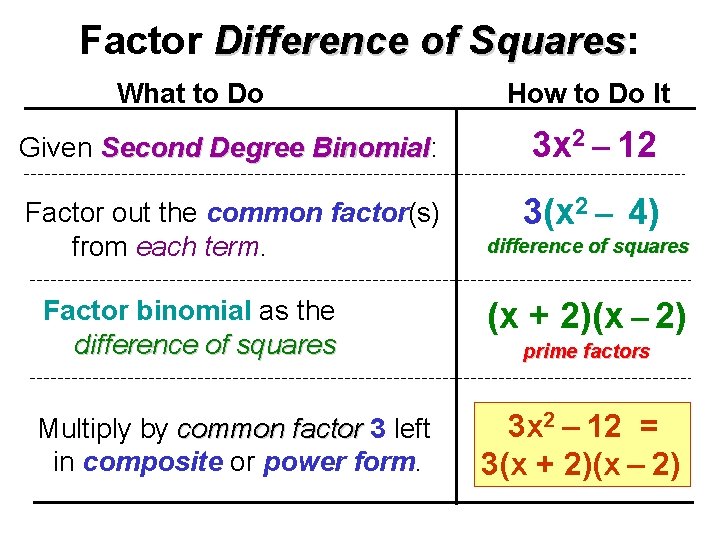
Factor Difference of Squares: Squares What to Do How to Do It Given Second Degree Binomial: Binomial 3 x 2 – 12 Factor out the common factor(s) from each term. 3(x 2 – 4) difference of squares Factor binomial as the difference of squares (x + 2)(x – 2) Multiply by common factor 3 left in composite or power form. 3 x 2 – 12 = 3(x + 2)(x – 2) prime factors
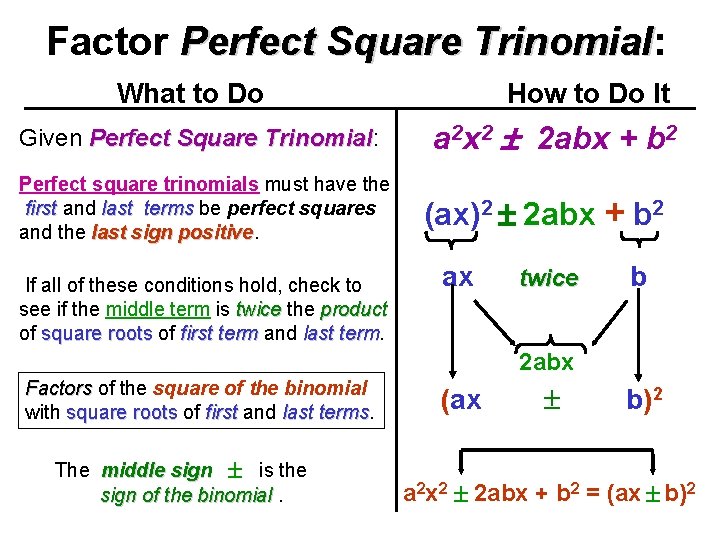
Factor Perfect Square Trinomial: Trinomial What to Do Given Perfect Square Trinomial: Trinomial Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term How to Do It a 2 x 2 2 abx + b 2 (ax)2 2 abx + b 2 ax twice b 2 abx Factors of the square of the binomial with square roots of first and last terms The middle sign is the sign of the binomial. (ax b)2 a 2 x 2 2 abx + b 2 = (ax b)2
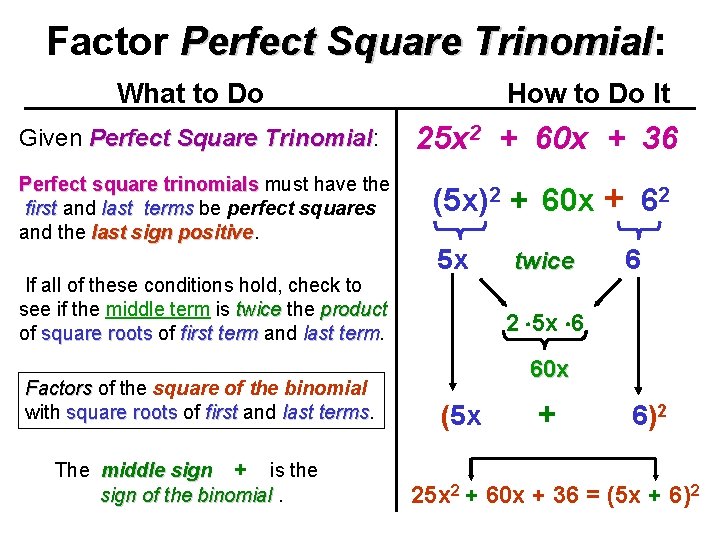
Factor Perfect Square Trinomial: Trinomial What to Do How to Do It Given Perfect Square Trinomial: Trinomial 25 x 2 + 60 x + 36 Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive (5 x)2 + 60 x + 62 If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term Factors of the square of the binomial with square roots of first and last terms The middle sign + is the sign of the binomial. 5 x twice 6 2 5 x 6 60 x (5 x + 6)2 25 x 2 + 60 x + 36 = (5 x + 6)2
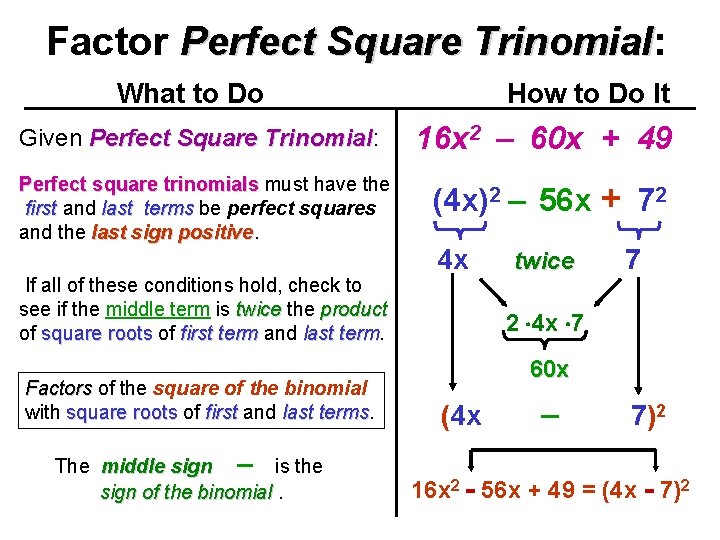
Factor Perfect Square Trinomial: Trinomial What to Do How to Do It Given Perfect Square Trinomial: Trinomial 16 x 2 – 60 x + 49 Perfect square trinomials must have the first and last terms be perfect squares and the last sign positive (4 x)2 – 56 x + 72 If all of these conditions hold, check to see if the middle term is twice the product of square roots of first term and last term Factors of the square of the binomial with square roots of first and last terms The middle sign – is the sign of the binomial. 4 x twice 7 2 4 x 7 60 x (4 x – 7)2 16 x 2 - 56 x + 49 = (4 x - 7)2
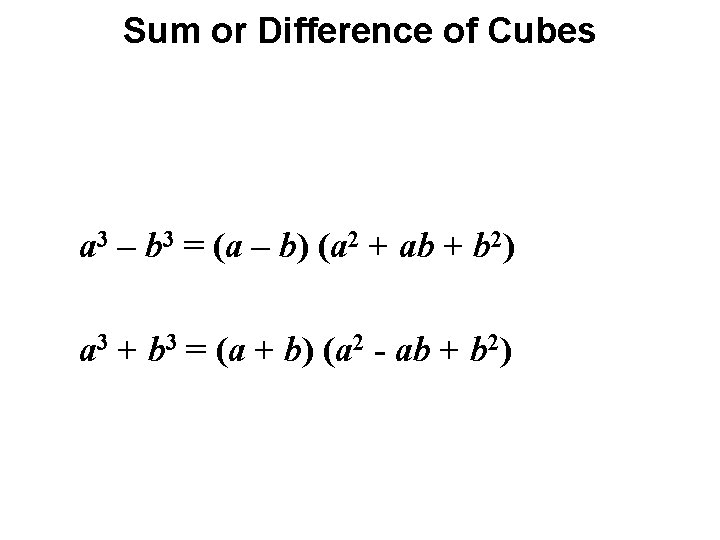
Sum or Difference of Cubes a 3 – b 3 = (a – b) (a 2 + ab + b 2) a 3 + b 3 = (a + b) (a 2 - ab + b 2)

Factoring Sums & Differences of Cubes 3 x + 64 =
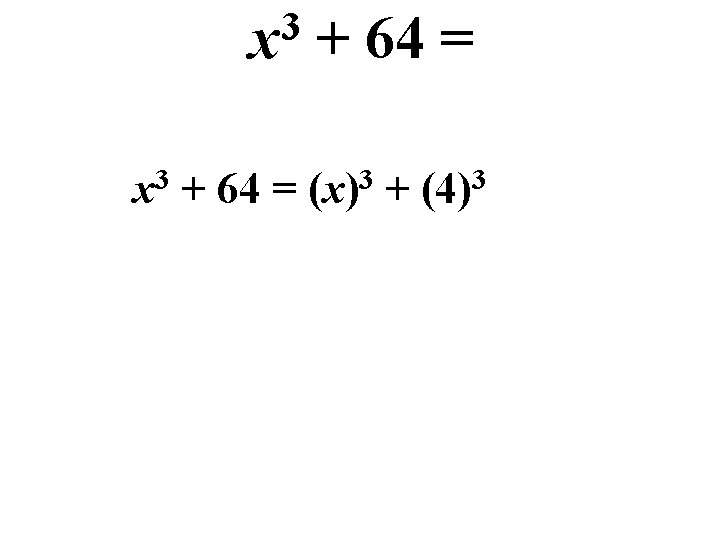
3 x + 64 = x 3 + 64 = (x)3 + (4)3
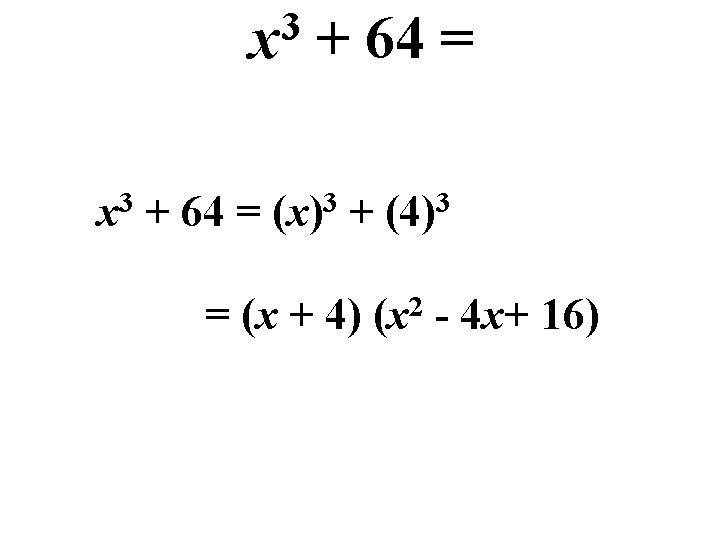
3 x + 64 = x 3 + 64 = (x)3 + (4)3 = (x + 4) (x 2 - 4 x+ 16)

Factoring Sums & Differences of Cubes z 3 - 1
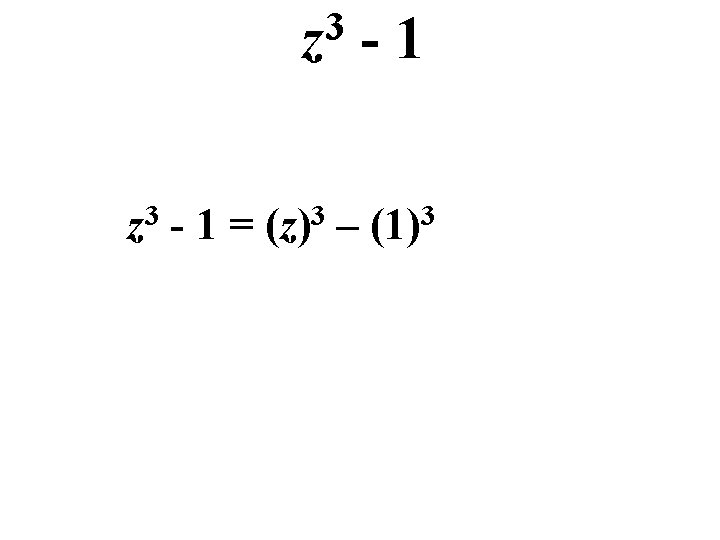
3 z -1 z 3 - 1 = (z)3 – (1)3
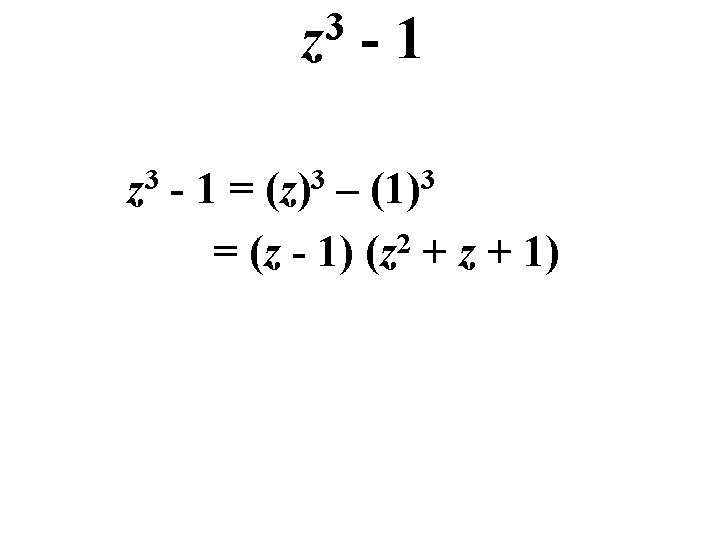

3 27 x Factor + 64
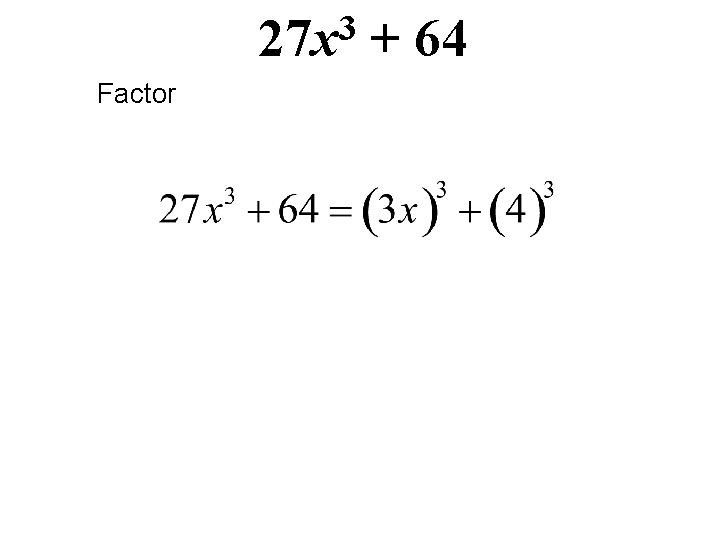
3 27 x Factor + 64
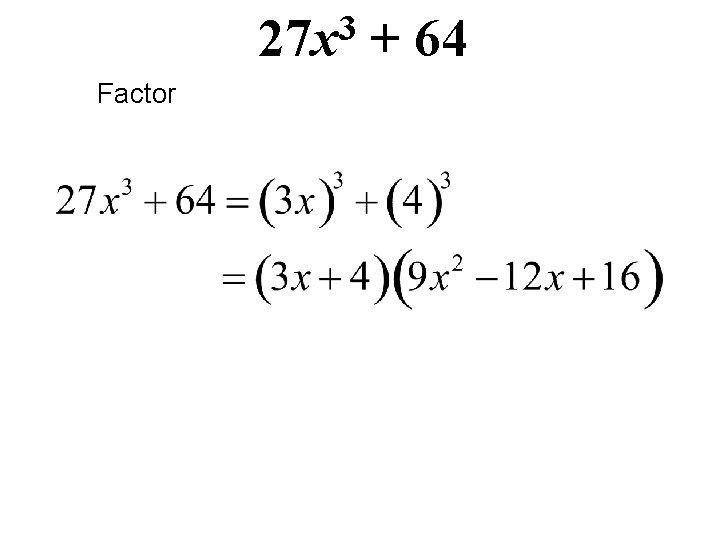
3 27 x Factor + 64

5. 4 THE END
- Slides: 32