Beginning Algebra 5 3 More Trinomials to Factor

Beginning Algebra 5. 3 More Trinomials to Factor

6. 3 More Trinomials to Factor Objective 1. To factor a trinomial whose leading coefficient is other than 1. Objective 2. To factor a polynomial by first factoring out the greatest common factor and then factoring the polynomial that remains.

Clue of Signs Same sign + Sum Ax 2 Bx C Larger sign – Difference Read as + or –
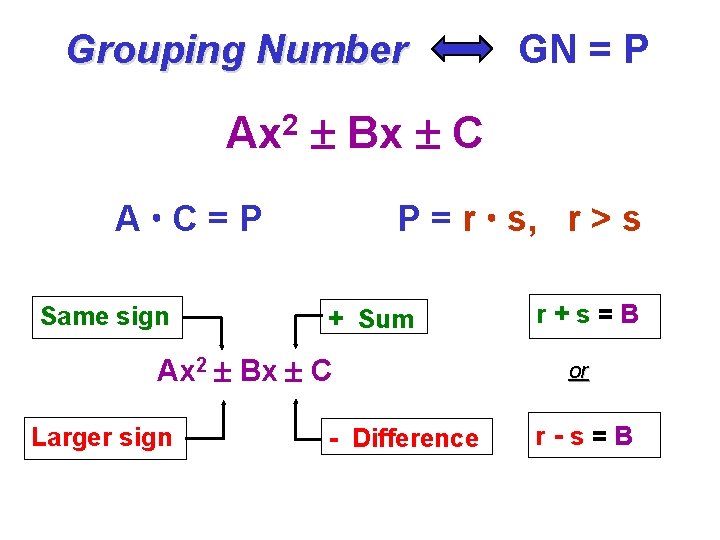
Grouping Number 2 Ax Bx C A C=P Same sign P = r s, r > s + Sum Ax 2 Bx C Larger sign GN = P - Difference r+s=B or r-s=B

Factor general quadratic trinomial: What to do Given a general quadratic trinomial: trinomial 1. Find the product of the first and last coefficients: coefficients A and C 2. Find all of the pairs of factors r and s 3. so their sum or difference is the middle coefficient. How to do it Ax 2 Bx C A C = P P = r s, r > s r+s=B or r-s=B

Factor by Clue of Signs: Signs What to Do How to Do It Given general trinomial of type that has no common factor. Read the clues of the signs [Read as “+ or ” ] Same sign + C Ax 2 Bx Larger sign The product P = A A C is the grouping number Find all possible factors of GN = P whose sum or difference is B and Bx: factor by grouping Difference P = r s , r > s + sum difference Rewrite middle term Sum (r + s) = B (r ‑s) = B Ax 2 rx sx + C (ax b)(cx d)

Example: 10 x 2 + 11 x - 6 What to do How to do it 1. Find the product of 10 and 6: 2. Find all of the pairs of factors: r and s with the difference = 11. 15 - 4 =11 3. Middle sign is + therefore: 4. Separate middle term 11 x: 10 · 6 = 60 60 = 60 · 1 30 · 2 20 · 3 15 · 4 12 · 5 10 · 6 +15 , - 4 +15 x , - 4 x

Example: 10 x 2 + 11 x - 6 What to do 5. Copy the polynomial: 6. Rewrite middle term 11 x: and group for factoring How to do it 10 x 2 + 11 x - 6 10 x 2 + 15 x - 4 x - 6 7. Factor each group: group bring down middle sign 5 x(2 x + 3) - 2(2 x + 3) 8. Factor common factor: factor (5 x - 2)(2 x + 3)
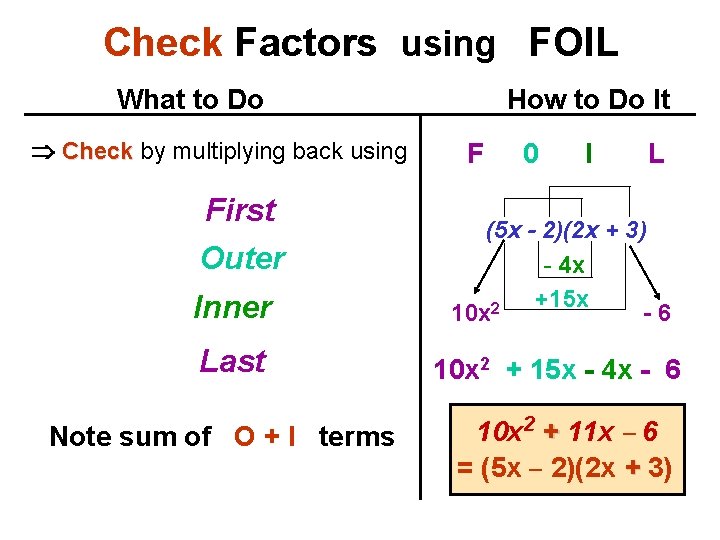
Check Factors using FOIL What to Do Check by multiplying back using First Outer How to Do It F 0 I L Inner (5 x - 2)(2 x + 3) - 4 x +15 x 2 10 x -6 Last 10 x 2 + 15 x - 4 x - 6 Note sum of O + I terms 10 x 2 + 11 x 6 = (5 x 2)(2 x + 3)

Example: 3 x 2 - 7 x - 6 What to do How to do it 1. Find the product of 3 and 6: 2. Find all of the pairs of factors: r and s with the difference = 7. 9 -2=7 3. Middle sign - is larger sign: sign 4. Separate middle term - 7 x: 3 · 6 = 18 18 = 18 · 1 9· 2 6· 3 -9, +2 - 9 x , + 2 x

Example: 3 x 2 - 7 x - 6 What to do 5. Copy the polynomial: How to do it 3 x 2 - 7 x - 6 6. Rewrite middle term -7 x: and group for factoring 3 x 2 - 9 x + 2 x - 6 7. Factor each group: group bring down middle sign 3 x(x - 3) + 2(x - 3) 8. Factor common factor: factor (3 x + 2)(x - 3)
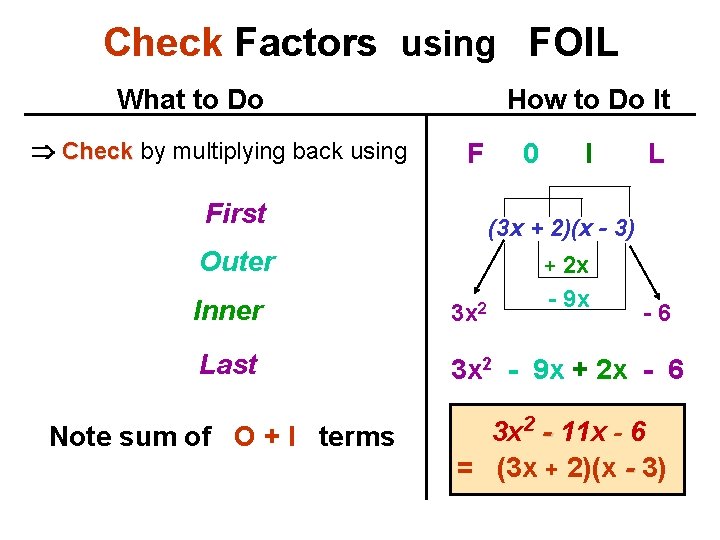
Check Factors using FOIL What to Do Check by multiplying back using How to Do It F First 0 I L (3 x + 2)(x - 3) Outer 2 x - 9 x + Inner 3 x 2 Last 3 x 2 - 9 x + 2 x - 6 Note sum of O + I terms 3 x 2 - 11 x - 6 = (3 x + 2)(x - 3) -6

Example: 3 x 2 - 11 xy + 6 y 2 What to do How to do it 1. Look at numbers only Find the product of 3 and 6: 2. Find all of the pairs of factors: r and s 3 · 6 = 18 18 = 18 · 1 9· 2 with the sum = 11. 6· 3 9 + 2 = 11 3. Middle sign - is same sign: sign 4. Separate middle term - 11 xy: -9, -2 - 9 xy , - 2 xy

Example: 3 x 2 - 11 xy + 6 y 2 What to do 5. Copy the polynomial: How to do it 3 x 2 - 11 xy + 6 y 2 6. Rewrite middle term -11 xy: and group for factoring 3 x 2 - 9 xy - 2 xy + 6 y 2 7. Factor each group: group bring down middle sign 3 x(x - 3 y) - 2(x - 3 y) 8. Factor common factor: factor (3 x - 2 y)(x - 3 y)
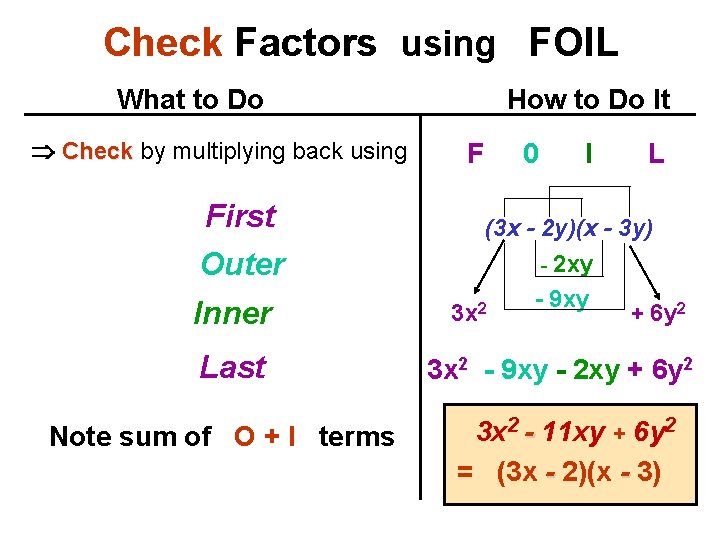
Check Factors using FOIL What to Do Check by multiplying back using First Outer Inner Last Note sum of O + I terms How to Do It F 0 I L (3 x - 2 y)(x - 3 y) - 2 xy - 9 xy 2 3 x + 6 y 2 3 x 2 - 9 xy - 2 xy + 6 y 2 3 x 2 - 11 xy + 6 y 2 = (3 x - 2)(x - 3)

Example: 6 t 2 + 23 t + 20 What to do How to do it 1. Find the product of 6 and 20: GN: 6 · 20 = 120 2. Find all of the pairs of factors: r and s 24 · 5 20 · 6 60 · 2 40 · 3 15 · 8 15 + 8 = 23 30 · 4 12 · 10 + is same sign: sign +15 , with the sum = 23. 3. Middle sign 120 · 1 4. Separate middle term 23 t: 120 +8 +15 t , + 8 t

Example: 6 t 2 + 23 t + 20 What to do 5. Copy the trinomial: How to do it 6 t 2 + 23 t + 20 6. Rewrite middle term 23 t: and group for factoring 6 t 2 + 15 t + 8 t - 20 7. Factor each group: group bring down middle sign 3 t(2 t + 5) + 4(2 t + 5) 8. Factor common factor: factor (3 t + 4)(2 t + 5)
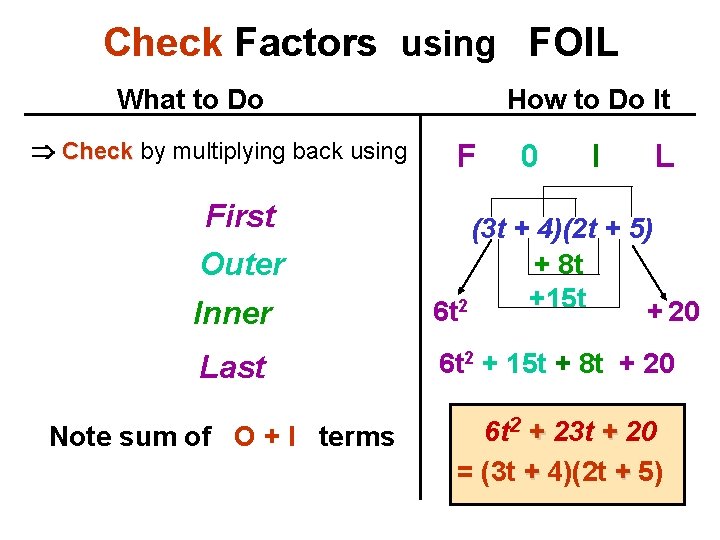
Check Factors using FOIL What to Do Check by multiplying back using First Outer How to Do It F 0 I L Inner (3 t + 4)(2 t + 5) + 8 t +15 t 6 t 2 + 20 Last 6 t 2 + 15 t + 8 t + 20 Note sum of O + I terms 6 t 2 + 23 t + 20 = (3 t + 4)(2 t + 5)

Trinomials with Common Factors: Factors Ax 2 Bx C What to Do 1. Factor out the common factor(s) from each term 2. Apply the distributive property 3. As common factors numbers are left in composite form and letters are left in power form 4. Check Inner Polynomial for Clue of Signs and GN How to Do It k·ax 2 k·bx k·c k·(ax 2 bx c) ax 2 bx c

Trinomials with Common Factors: Factors 12 x 2 y - 33 xy + 9 y What to Do How to Do It 1. Factor out the common factor(s) 2 - 3 y· 11 x + 3 y· 3 3 y· 4 x from each term. 2. Apply the distributive property 3 y(4 x 2 - 11 x + 3) 3. As common factors numbers are left in composite form and letters are left in power form 4. Check Inner Polynomial for Clue of Signs and GN 4 x 2 - 11 x + 3

Inner Trinomial: 4 x 2 - 11 x - 3 What to do How to do it 1. Find the product of 4 and 3: 2. Find all of the pairs of factors: r and s with the difference = 11. 12 - 1 = 11 3. Middle sign – is larger sign: sign 4. Separate middle term - 11 x: 4 · 3 = 12 12 = 12 · 1 6· 2 4· 3 - 12 , + 1 - 12 x , + 1 x

Inner Trinomial: 4 x 2 - 11 x - 3 What to do 5. Copy the trinomial: 6. Rewrite middle term -11 x: and group for factoring 7. Factor each group: group bring down middle sign 8. Factor common factor: factor How to do it 4 x 2 - 11 x - 3 4 x 2 - 12 x + 1 x - 3 4 x(x - 3) + 1(x - 3) (4 x + 1)(x - 3) Complete: Complete Multiply common factor 3 y 3 y(4 x + 1)(x - 3)
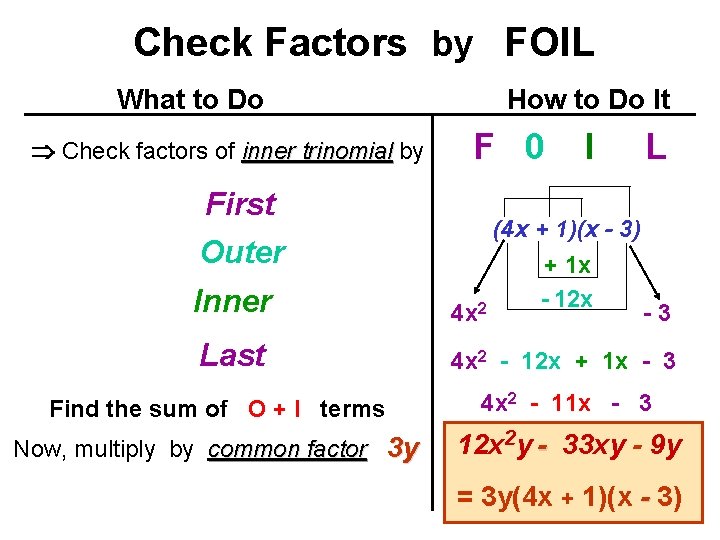
Check Factors by FOIL What to Do Check factors of inner trinomial by How to Do It F 0 First Outer I (4 x + 1)(x - 3) + 1 x - 12 x 2 L Inner 4 x Last 4 x 2 - 12 x + 1 x - 3 -3 Find the sum of O + I terms 4 x 2 - 11 x - 3 Now, multiply by common factor 3 y 12 x 2 y - 33 xy - 9 y = 3 y(4 x + 1)(x - 3)

5. 3 THE END
- Slides: 24