Beamdiagnostics by Beamstrahlung Pair Analysis C Grah DESY

Beamdiagnostics by Beamstrahlung Pair Analysis C. Grah – DESY FCAL Collaboration Workshop MPI Munich, 17 th October 2006 17 -Oct-2006 C. Grah: Beamdiagnostics

Content Ø Overview – Geometries and Parameter Sets Ø Beamstrahlung Pair Analysis Ø Results of Pair Analysis – Comparison between 2 mrad, and 14 mrad for different magnetic field configurations Ø Look on the Geant 4 Simulation Be. Ca. S and first results (A. Sapronov) 17 -Oct-2006 C. Grah: Beamdiagnostics 2
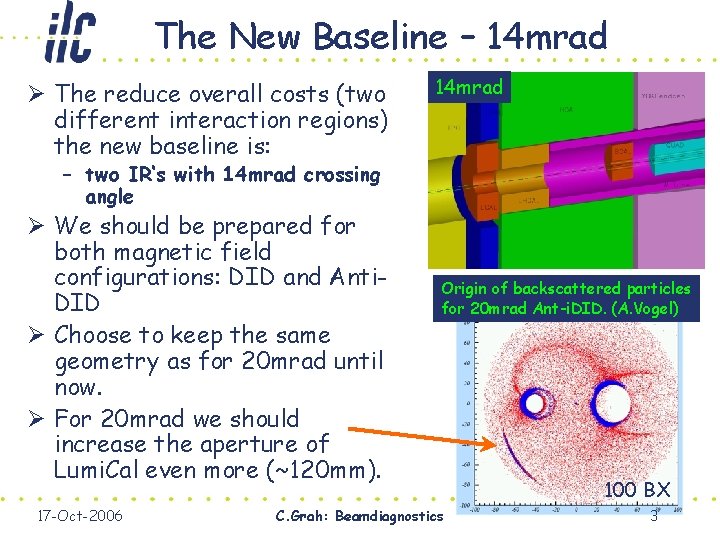
The New Baseline – 14 mrad Ø The reduce overall costs (two different interaction regions) the new baseline is: 14 mrad – two IR‘s with 14 mrad crossing angle Ø We should be prepared for both magnetic field configurations: DID and Anti. DID Ø Choose to keep the same geometry as for 20 mrad until now. Ø For 20 mrad we should increase the aperture of Lumi. Cal even more (~120 mm). 17 -Oct-2006 Origin of backscattered particles for 20 mrad Ant-i. DID. (A. Vogel) C. Grah: Beamdiagnostics 100 BX 3
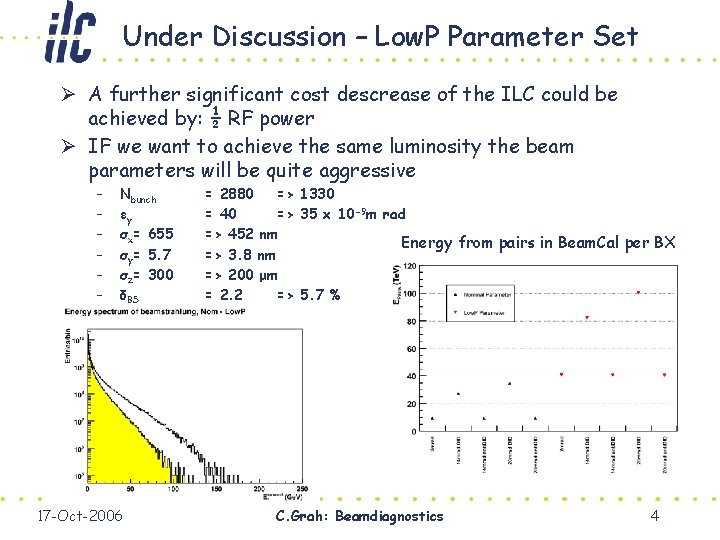
Under Discussion – Low. P Parameter Set Ø A further significant cost descrease of the ILC could be achieved by: ½ RF power Ø IF we want to achieve the same luminosity the beam parameters will be quite aggressive – – – Nbunch εy σx= 655 σy = 5. 7 σz = 300 δBS 17 -Oct-2006 = 2880 => 1330 = 40 => 35 x 10 -9 m rad => 452 nm Energy from pairs in Beam. Cal per BX => 3. 8 nm => 200 μm = 2. 2 => 5. 7 % C. Grah: Beamdiagnostics 4
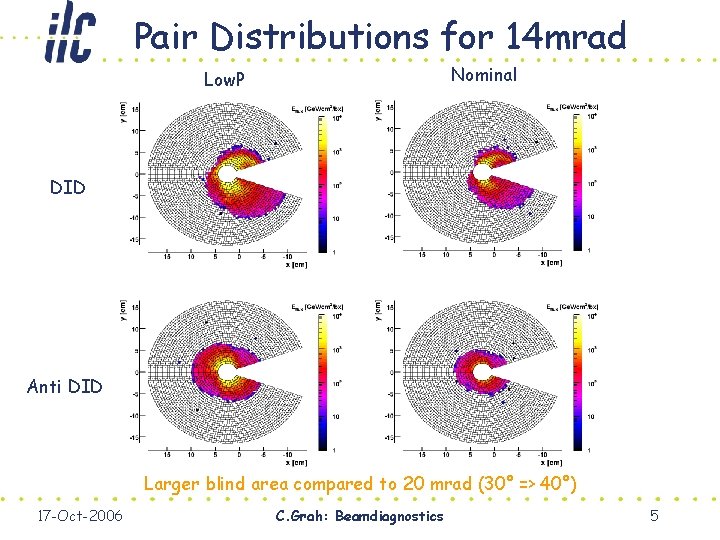
Pair Distributions for 14 mrad Nominal Low. P DID Anti DID Larger blind area compared to 20 mrad (30° => 40°) 17 -Oct-2006 C. Grah: Beamdiagnostics 5
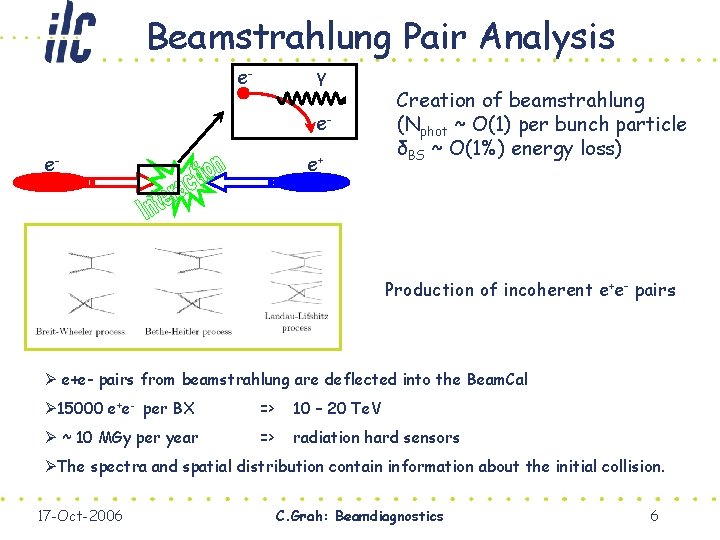
Beamstrahlung Pair Analysis γ e- e+ Creation of beamstrahlung (Nphot ~ O(1) per bunch particle δBS ~ O(1%) energy loss) Production of incoherent e+e- pairs Ø e+e- pairs from beamstrahlung are deflected into the Beam. Cal Ø 15000 e+e- per BX => 10 – 20 Te. V Ø ~ 10 MGy per year => radiation hard sensors ØThe spectra and spatial distribution contain information about the initial collision. 17 -Oct-2006 C. Grah: Beamdiagnostics 6
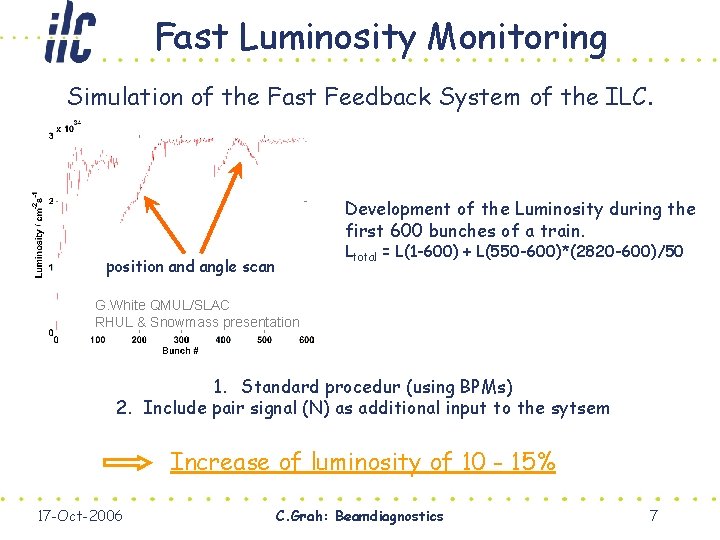
Fast Luminosity Monitoring Simulation of the Fast Feedback System of the ILC. Development of the Luminosity during the first 600 bunches of a train. Ltotal = L(1 -600) + L(550 -600)*(2820 -600)/50 position and angle scan G. White QMUL/SLAC RHUL & Snowmass presentation 1. Standard procedur (using BPMs) 2. Include pair signal (N) as additional input to the sytsem Increase of luminosity of 10 - 15% 17 -Oct-2006 C. Grah: Beamdiagnostics 7
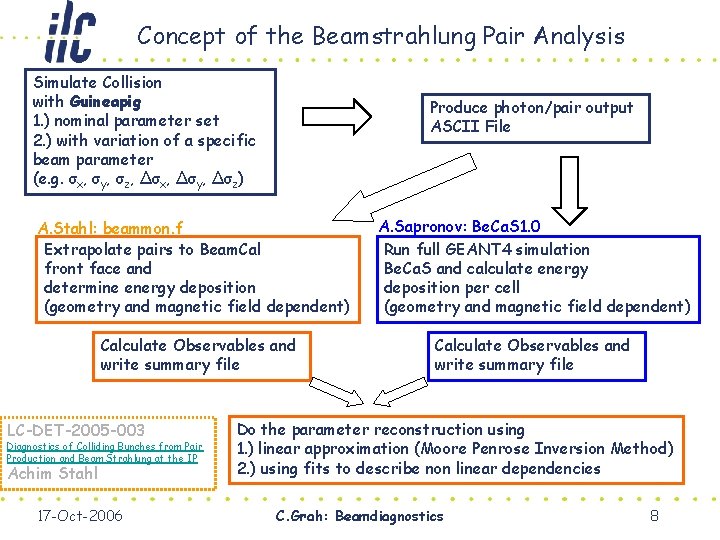
Concept of the Beamstrahlung Pair Analysis Simulate Collision with Guineapig 1. ) nominal parameter set 2. ) with variation of a specific beam parameter (e. g. σx, σy, σz, Δσx, Δσy, Δσz) Produce photon/pair output ASCII File A. Stahl: beammon. f Extrapolate pairs to Beam. Cal front face and determine energy deposition (geometry and magnetic field dependent) Calculate Observables and write summary file LC-DET-2005 -003 Diagnostics of Colliding Bunches from Pair Production and Beam Strahlung at the IP Achim Stahl 17 -Oct-2006 A. Sapronov: Be. Ca. S 1. 0 Run full GEANT 4 simulation Be. Ca. S and calculate energy deposition per cell (geometry and magnetic field dependent) Calculate Observables and write summary file Do the parameter reconstruction using 1. ) linear approximation (Moore Penrose Inversion Method) 2. ) using fits to describe non linear dependencies C. Grah: Beamdiagnostics 8
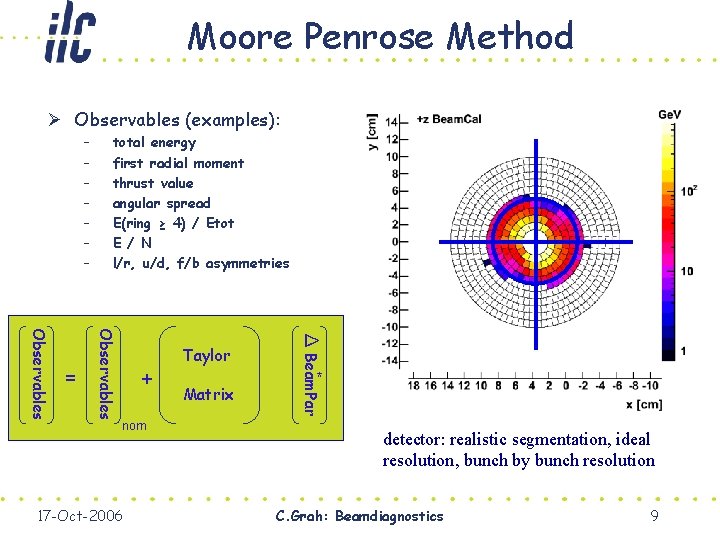
Moore Penrose Method Ø Observables (examples): – – – – Taylor + nom 17 -Oct-2006 Matrix Δ Beam. Par Observables = total energy first radial moment thrust value angular spread E(ring ≥ 4) / Etot E / N l/r, u/d, f/b asymmetries * detector: realistic segmentation, ideal resolution, bunch by bunch resolution C. Grah: Beamdiagnostics 9
![observable j [au] 1 st order Taylor Matrix parametrization (polynomial) slope at nom. value observable j [au] 1 st order Taylor Matrix parametrization (polynomial) slope at nom. value](http://slidetodoc.com/presentation_image_h2/ebc565ca537f79218d9ed941f6150c7a/image-10.jpg)
observable j [au] 1 st order Taylor Matrix parametrization (polynomial) slope at nom. value taylor coefficient i, j 1 point = 1 bunch crossing by guinea-pig beam parameter i [au] 17 -Oct-2006 C. Grah: Beamdiagnostics 10
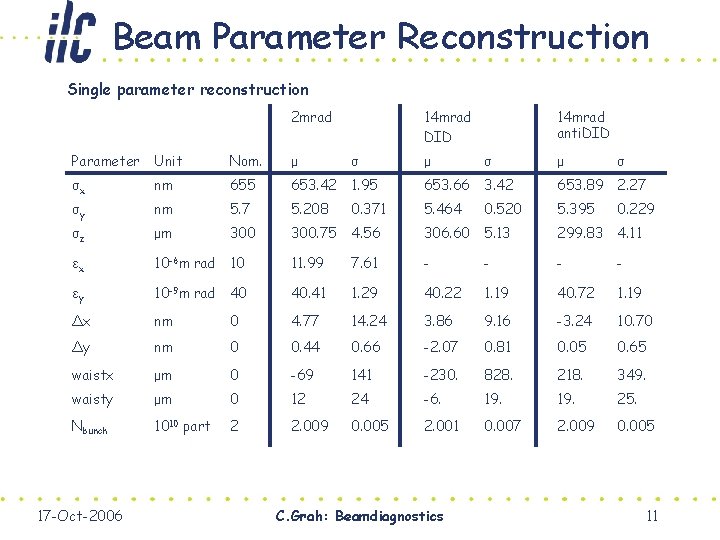
Beam Parameter Reconstruction Single parameter reconstruction 2 mrad 14 mrad DID 14 mrad anti. DID Parameter Unit Nom. μ σ μ σ σx nm 655 653. 42 1. 95 653. 66 3. 42 653. 89 2. 27 σy nm 5. 7 5. 208 0. 371 5. 464 0. 520 5. 395 0. 229 σz μm 300. 75 4. 56 306. 60 5. 13 299. 83 4. 11 εx 10 -6 m rad 10 11. 99 7. 61 - - εy 10 -9 m rad 40 40. 41 1. 29 40. 22 1. 19 40. 72 1. 19 Δx nm 0 4. 77 14. 24 3. 86 9. 16 -3. 24 10. 70 Δy nm 0 0. 44 0. 66 -2. 07 0. 81 0. 05 0. 65 waistx μm 0 -69 141 -230. 828. 218. 349. waisty μm 0 12 24 -6. 19. 25. Nbunch 1010 part 2 2. 009 0. 005 2. 001 0. 007 2. 009 0. 005 17 -Oct-2006 C. Grah: Beamdiagnostics 11
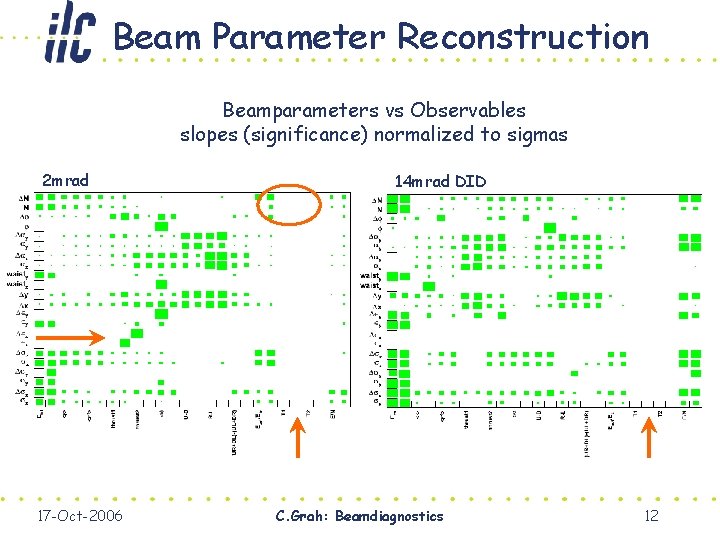
Beam Parameter Reconstruction Beamparameters vs Observables slopes (significance) normalized to sigmas 2 mrad 17 -Oct-2006 14 mrad DID C. Grah: Beamdiagnostics 12
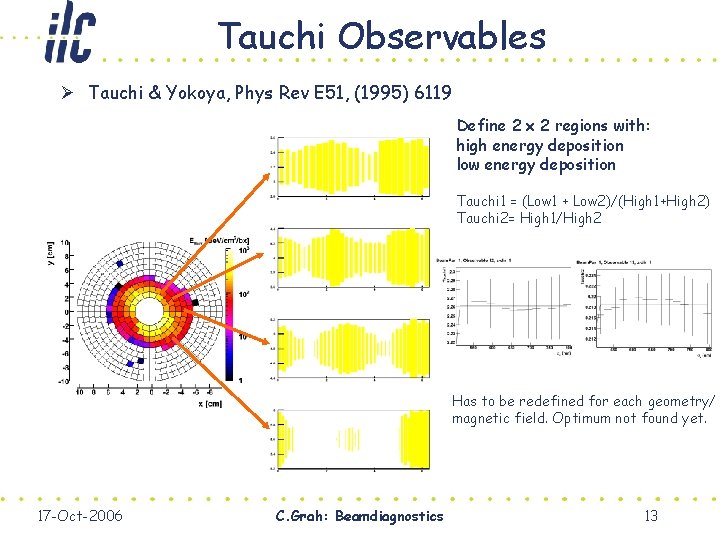
Tauchi Observables Ø Tauchi & Yokoya, Phys Rev E 51, (1995) 6119 Define 2 x 2 regions with: high energy deposition low energy deposition Tauchi 1 = (Low 1 + Low 2)/(High 1+High 2) Tauchi 2= High 1/High 2 Has to be redefined for each geometry/ magnetic field. Optimum not found yet. 17 -Oct-2006 C. Grah: Beamdiagnostics 13

Geant 4 Simulation - Be. Ca. S Ø A Geant 4 Beam. Cal simulation has been set up by A. Sapronov. Ø Energy distribution for 2 mrad and 20 mrad DID (14 mrad not yet simulated). Ø Be. Ca. S can be configured to run with: – different crossing angles (according geometry is chosen) – magnetic field (solenoid, (Anti) DID, use field map – detailed material composition of Beam. Cal including sensors with metallization, absorber, PCB, air gap 17 -Oct-2006 C. Grah: Beamdiagnostics 2 mrad 20 mrad 14
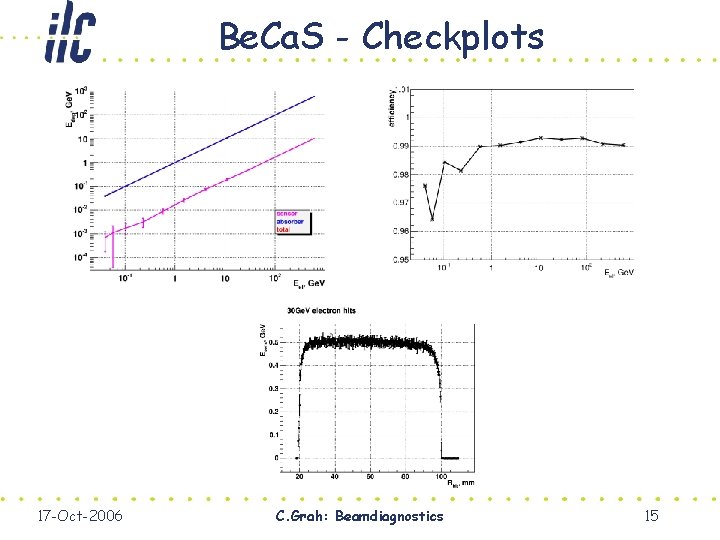
Be. Ca. S - Checkplots 17 -Oct-2006 C. Grah: Beamdiagnostics 15
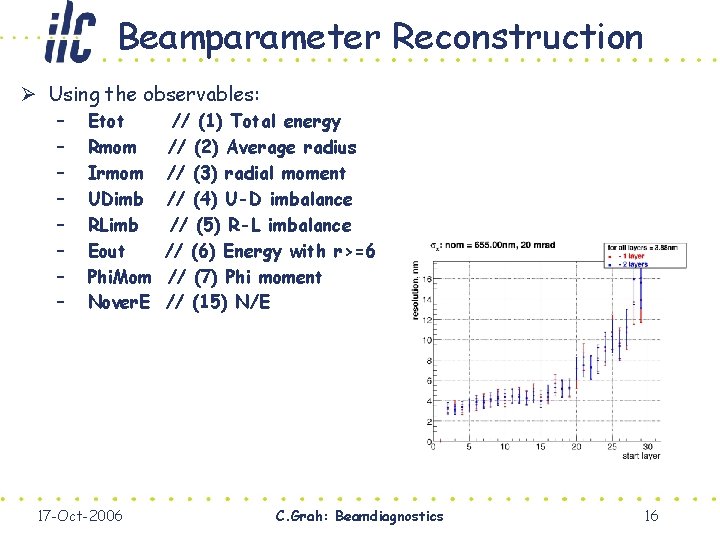
Beamparameter Reconstruction Ø Using the observables: – – – – Etot Rmom Irmom UDimb RLimb Eout Phi. Mom Nover. E 17 -Oct-2006 // (1) Total energy // (2) Average radius // (3) radial moment // (4) U-D imbalance // (5) R-L imbalance // (6) Energy with r>=6 // (7) Phi moment // (15) N/E C. Grah: Beamdiagnostics 16

Summary Ø The geometry for a 14 mrad beam crossing angle is the same as for 20 mrad. The 20 mrad geometry should be changed due to background. Ø The Low. P parameter set is under discussion => lower L or higher background. Ø Consolidated guineapig steering parameters and reproduced pair/photon files. Ø Tested 2, 14 and 20 mrad configurations with DID/Anti. DID field. Ø Found small significance of the Tauchi variables. Ø A Geant 4 simulation of Beam. Cal (Be. Ca. S) is ready for usage. First tests show that a subset of the detector information seems sufficient for beam parameter reconstruction. – Include this into Mokka – Build additional fast FCAL simulation (? ) 17 -Oct-2006 C. Grah: Beamdiagnostics 17
- Slides: 17