Beam deflection with using volume reflection in bent

Beam deflection with using volume reflection in bent crystals ------------------------------------● Limitation of reflection efficiency due to volume capture ● Probability for fast stage of volume capture – nuclear stage ● Sequence of Volume Reflectors – parallel and unparallel SVR ● Unparallel SVR for 7 -Te. V protons – optimization by increasing a bend angle from the first up to the last crystal of SVR ● Possibility to reduce non-reflected fraction volume capture reduce due to increasing curvature along a crystal

Volume reflection of high-energy charged particles in a bent crystal ---------------------------------------A. M. Taratin and S. A. Vorobiev. Phys. Letters A 119 (1987) 425. Nucl. Instrum. Meth. B 26 (1987) 512. Incident angles of particles - θo > θc There is a place in the crystal where a particle momentum is tangent to the planes Particle reflection occurs from a bent plane Quasi-channeled particles are deflected to the side opposite to the bend Deflection angle is determined by the critical angle – θvr=k θc , k < 2

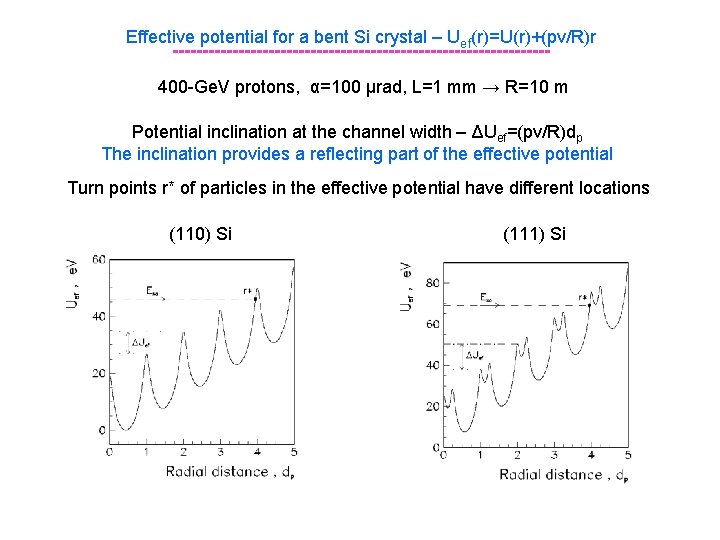
Effective potential for a bent Si crystal – Uef(r)=U(r)+(pv/R)r -------------------------------400 -Ge. V protons, α=100 μrad, L=1 mm → R=10 m Potential inclination at the channel width – ΔUef=(pv/R)dp The inclination provides a reflecting part of the effective potential Turn points r* of particles in the effective potential have different locations (110) Si (111) Si

Volume reflection has no 100% efficiency ------------------------Volume capture of particles can occur near the turn points in the effective potential due to multiple scattering by the crystal electrons and nuclei For shot crystals particles are captured on high levels in the potential well VC probability is ~ 1% and much higher than the estimation – Pvc = Rθc/Le Non-reflected part ΔN+ are particles deflected to the bend side → VC tail ΔN+

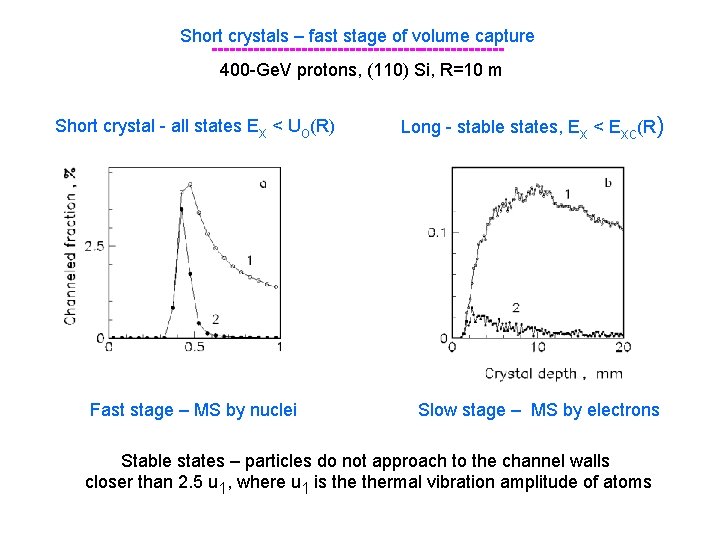
Short crystals – fast stage of volume capture ------------------------400 -Ge. V protons, (110) Si, R=10 m Short crystal - all states Ex < Uo(R) Fast stage – MS by nuclei Long - stable states, Ex < Exc(R) Slow stage – MS by electrons Stable states – particles do not approach to the channel walls closer than 2. 5 u 1, where u 1 is thermal vibration amplitude of atoms

Probability estimation for a fast stage of volume capture --------------------------------With using a nuclear dechanneling length Ln Uo – the potential well depth, Exc ─ the transverse energy critical for the existence of stable trajectories of channeled particles, LR ─ the radiation length Es=21 Me. V The value Pvc ≈ 7% for 400 -Ge. V protons in (110) Si with R=10 m From simulation – 6. 4%

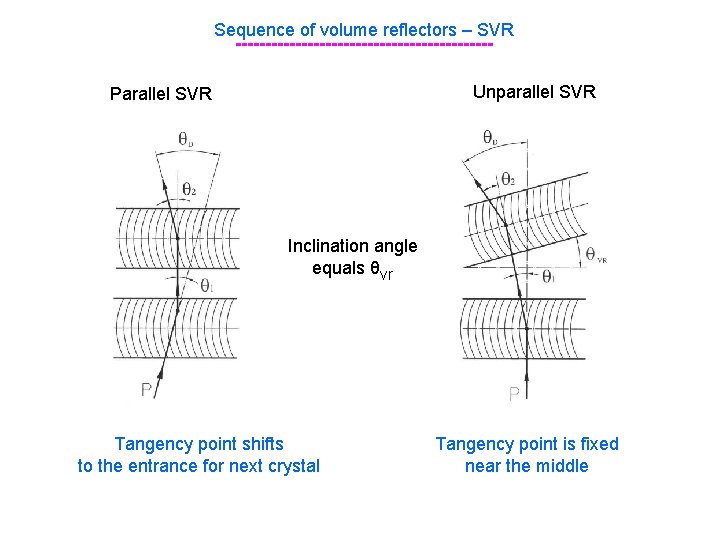
Sequence of volume reflectors – SVR ---------------------Unparallel SVR Parallel SVR Inclination angle equals θvr Tangency point shifts to the entrance for next crystal Tangency point is fixed near the middle

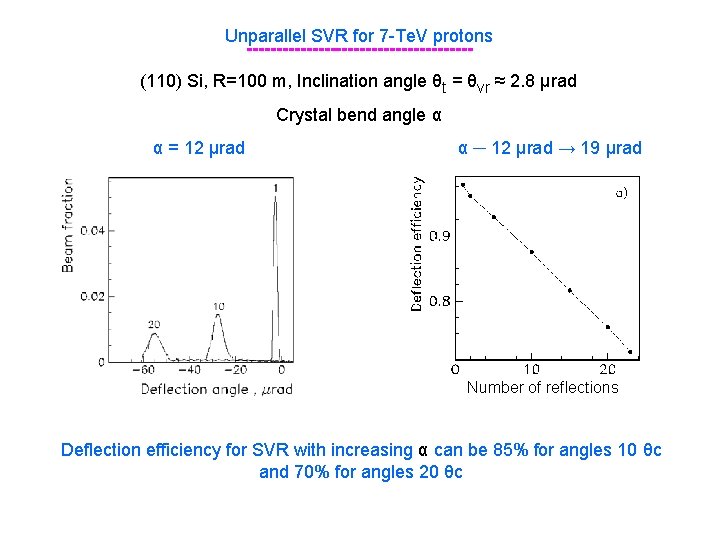
Unparallel SVR for 7 -Te. V protons -------------------(110) Si, R=100 m, Inclination angle θt = θvr ≈ 2. 8 μrad Crystal bend angle α α = 12 μrad α ─ 12 μrad → 19 μrad Number of reflections Deflection efficiency for SVR with increasing α can be 85% for angles 10 θc and 70% for angles 20 θc

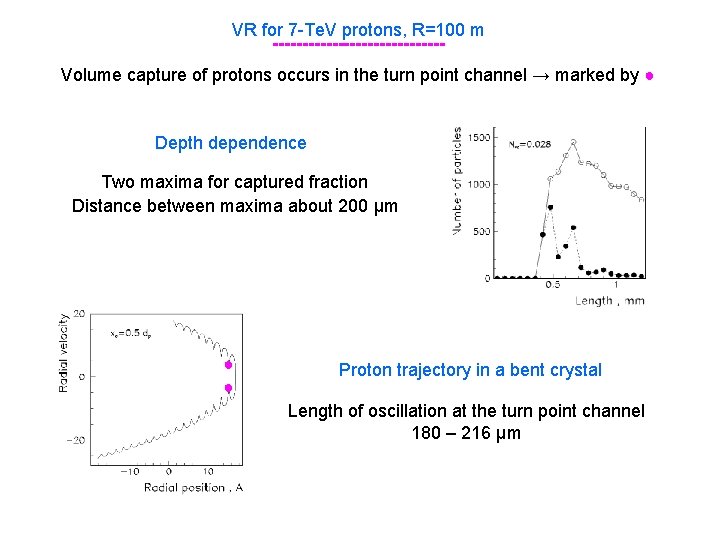
VR for 7 -Te. V protons, R=100 m --------------Volume capture of protons occurs in the turn point channel → marked by ● Depth dependence Two maxima for captured fraction Distance between maxima about 200 μm ● ● Proton trajectory in a bent crystal Length of oscillation at the turn point channel 180 – 216 μm

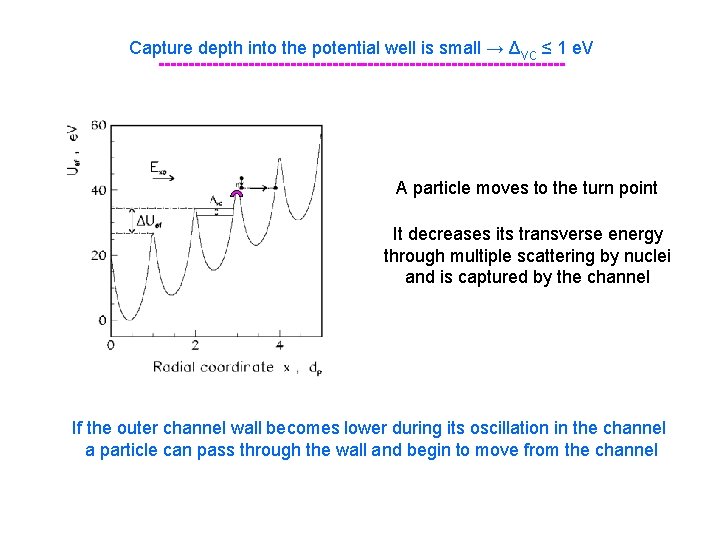
Capture depth into the potential well is small → Δvc ≤ 1 e. V ---------------------------------- A particle moves to the turn point It decreases its transverse energy through multiple scattering by nuclei and is captured by the channel If the outer channel wall becomes lower during its oscillation in the channel a particle can pass through the wall and begin to move from the channel

Possibility to avoid volume capture if the depth of the potential well reduces along the crystal -----------------------------Sufficient rate of the potential well reduce – Δvc/λ = 5 e. V/mm A similar condition for increasing the potential inclination Gives for a linear increase of the crystal curvature Radius change along the crystal length Lcr=1. 2 mm ─ Ro = 120 m → 78 m Corresponding increase of the potential inclination ─ 6 e. V and reduce of the potential well depth ─ 2. 2 e. V

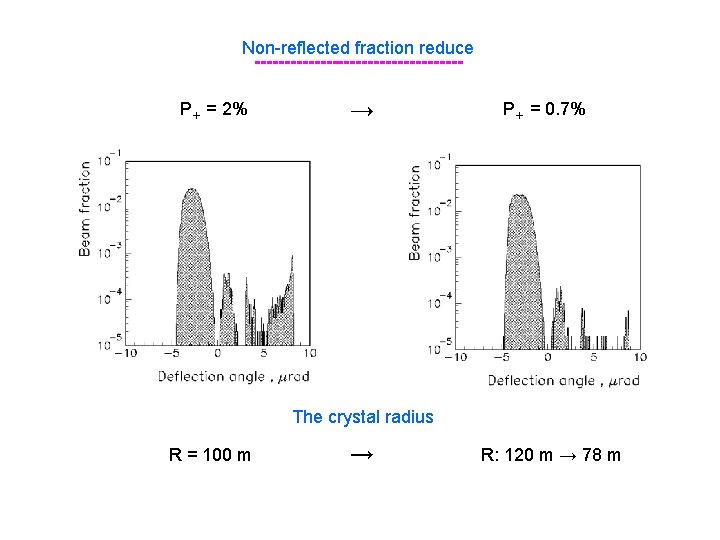
Non-reflected fraction reduce -----------------P+ = 2% → P+ = 0. 7% The crystal radius R = 100 m → R: 120 m → 78 m

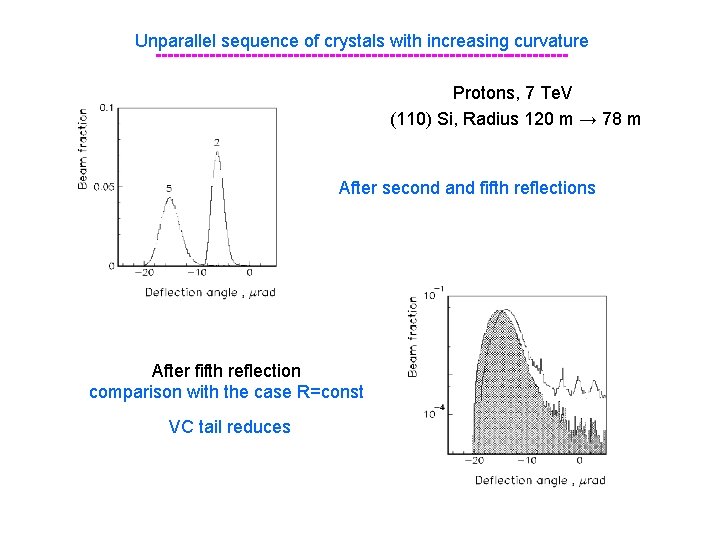
Unparallel sequence of crystals with increasing curvature ----------------------------------Protons, 7 Te. V (110) Si, Radius 120 m → 78 m After second and fifth reflections After fifth reflection comparison with the case R=const VC tail reduces

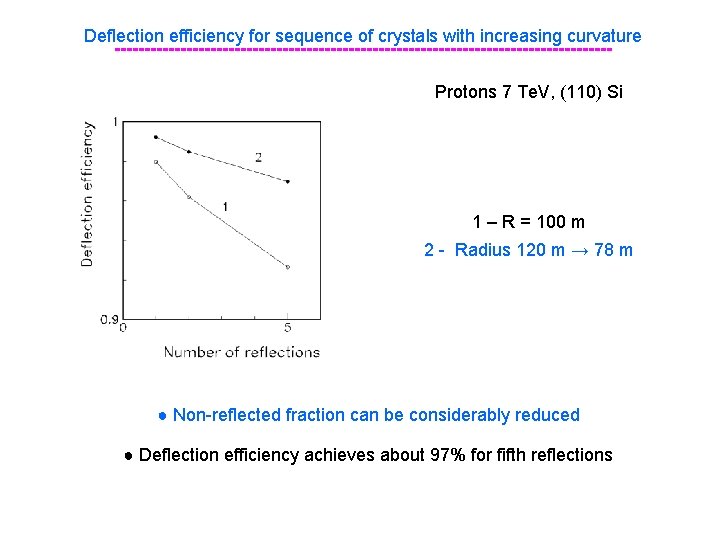
Deflection efficiency for sequence of crystals with increasing curvature -----------------------------------------Protons 7 Te. V, (110) Si 1 – R = 100 m 2 - Radius 120 m → 78 m ● Non-reflected fraction can be considerably reduced ● Deflection efficiency achieves about 97% for fifth reflections