Be seated before the bell rings Agenda DESK

Be seated before the bell rings Agenda: DESK homework Warm-up (in your notes) Review questions Part 2 ch 7 test (with calculators) Warmup Notes 8. 1

Notebook Table of content 19)Add, subtract, multiply polynomials 20) Dividing Polynomials 21) Factor and find roots Page 1 8. 1 Variation Functions 22) Fundamental Theorem of Algebra 23)Graph of polynomials 24) Radical Expressions and Rational Exponents 25) Variation Functions HW ; p. 573; 5, 8, 12, 16, 20 -23 1

Warm Up 11/26 Solve each equation. 2. 4 = 2 x 9 10. 8 2. 1. 6 x = 1. 8(24. 8) 27. 9 1. Determine whether each data set could represent a linear function. 3. x y 2 12 4 6 4. x y – 2 – 1 – 6 – 2 6 4 8 3 0 2 1 6 no yes

8. 1 Variation Functions A direct variation is a relationship between two variables x and y that can be written in the form y = kx, where k ≠ 0. constant of variation As x’s gets larger, y’s get larger by constant k.

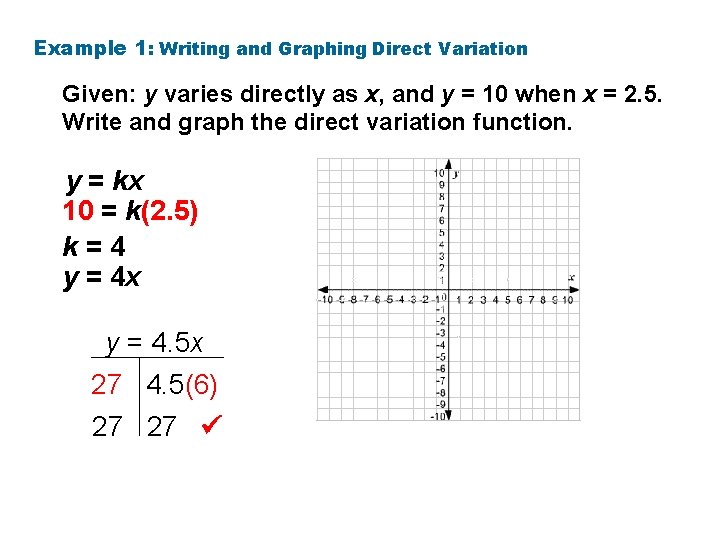
Example 1: Writing and Graphing Direct Variation Given: y varies directly as x, and y = 10 when x = 2. 5. Write and graph the direct variation function. y = kx 10 = k(2. 5) k=4 y = 4 x y = 4. 5 x 27 4. 5(6) 27 27

Example 2 A: Solving Direct Variation Problems The value of y varies directly with x. and y = 6 when x = 30. Find y when x =45. Method 1 Find k. y = kx 6 = k(30) 1/5 = k Method 2 Use a proportion. y 6 = 45 30 y 1 = 5 45 y = 1/5 x y = 1/5(45) y=9 5 y = 45/5 = 9

You try! Example 2 B The perimeter P of a regular dodecagon varies directly as the side length s, and P = 18 in. when s = 1. 5 in. Find s when P = 75 in. Method 1 Find k. P = ks 18 = k(1. 5) 12 = k P = 12 s 75 = 12 s 6. 25 ≈ s Method 2 Use a proportion. 18 75 = 1. 5 s 18 s = 112. 5 6. 25 = s

A joint variation is a relationship among three variables that can be written in the form y = kxz, where k is the constant of variation.

Example 3: Solving Joint Variation Problems The area A of a triangle varies jointly as the base B and the height h, and A = 20 m 2 when B = 5 m and h = 8 m. Find b when A = 60 m 2 and h = 6 ft. Step 1 Find k. A = k. Bh 20= k(5)(8) K = 1 2 Step 2 Use the variation function. 1 A = 2 Bh 1 60= 2 B(6) B = 20 The base is 20 meters.

You try ! Example 4 The lateral surface area L of a cone varies jointly as the area of the base radius r and the slant height l, and L = 63 m 2 when r = 3. 5 m and l = 18 m. Find r to the nearest tenth when L = 8 m 2 and l = 5 m. Step 1 Find k. L = krl 63 = k(3. 5)(18) =k Step 2 Use the variation function. L = rl 8 = r(5) 1. 6 = r

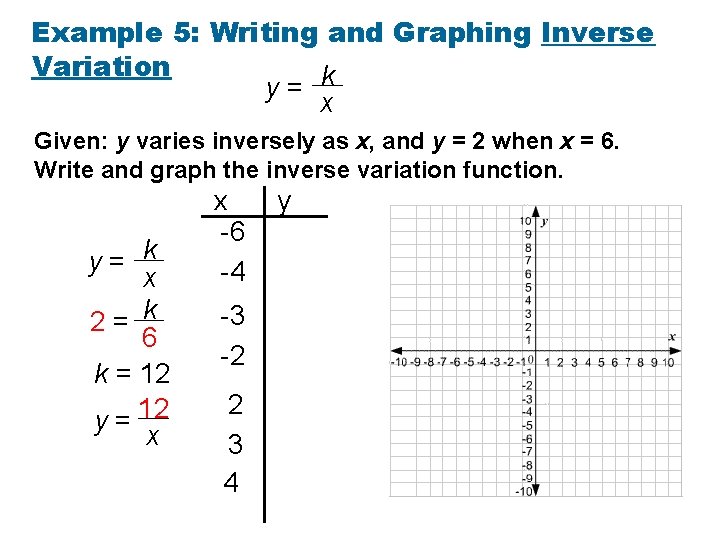
Example 5: Writing and Graphing Inverse Variation y= k x Given: y varies inversely as x, and y = 2 when x = 6. Write and graph the inverse variation function. y= k x 2= k 6 k = 12 y = 12 x x -6 -4 -3 -2 2 3 4 y

Example 6 A The time t that it takes for a group of volunteers to construct a house varies inversely as the number of volunteers v. If 20 volunteers can build a house in 62. 5 working hours, how many working hours would it take 15 volunteers to build a house? Find k. t= k v k 20 k = 1250 t= v 1250 t= 15 1 t ≈ 83 62. 5 = 3

Example 6 b: Sports Application The time t needed to complete a certain race varies inversely as the runner’s average speed s. If a runner with an average speed of 8. 82 mi/h completes the race in 2. 97 h, what is the average speed of a runner who completes the race in 3. 5 h? t= k s Find k. k Substitute. 2. 97 = 8. 82 Solve for k. k = 26. 1954 t = 26. 1954 s 3. 5 = 26. 1954 s s ≈ 7. 48 Use 26. 1954 for k. Substitute 3. 5 for t. Solve for s.

Example 7 combined variation The volume V of a gas varies inversely as the pressure P and directly as the temperature T. A certain gas has a volume of 10 liters (L), a temperature of 300 kelvins (K), and a pressure of 1. 5 atmospheres (atm). If the gas is heated to 400 K, and has a pressure of 1 atm, what is its volume? Step 1 Find k. V= 10 = 0. 05 = k k. T P k(300) 1. 5 Step 2 Use the variation function. V = 0. 05 T P V = 0. 05(400) (1) V = 20 The new volume will be 20 L.

You try! Example 8: Chemistry Application The change in temperature of an aluminum wire varies inversely as its mass m and directly as the amount of heat energy E transferred. The temperature of an aluminum wire with a mass of 0. 1 kg rises 5°C when 450 joules (J) of heat energy are transferred to it. How much heat energy must be transferred to an aluminum wire with a mass of 0. 2 kg raise its temperature 20°C? Step 1 Find k. ΔT = k. E m 5 = k(450) 0. 1 1 900 = k Step 2 Use the variation function. ΔT = E 900 m E 20 = 900(0. 2) 3600 = E The amount of heat energy that must be transferred is 3600 joules (J).