BCB 322 Landscape Ecology Lecture 2 Theories Models

BCB 322: Landscape Ecology Lecture 2: Theories & Models Hierarchy theory, diffusion theory & percolation theory

Introduction • Landscape heterogeneity, complexity of the ecosystem components, resource restraints & population behaviour all affect organisms in a landscape. • The interaction of these components is estimated through several models and theories. • Most of these theories evolved in different contexts • All aim to interpret landscape complexity (systems & structures), and together

Principal theories • We shall be looking at four theories in greater detail: – – Island biogeography theory Hierarchy theory Diffusion theory Percolation theory • We’ll also consider two models: – Metapopulation model – Source-sink systems model • Between them these models cover a lot of the conceptual ground of landscape ecology • There is considerable variation in the details of some of the models

Hierarchy theory • Landscapes are intrinsically complex, with variation in resources at all scales • Hierarchy theory attempts to explain how scale-specific components of the landscape are in contact with components visible at other resolutions • HT considers that any system is a component of other systems at a larger scale, and is itself comprised of sub-systems. • eg: Landscape classification, with the micro-, meso-, macro- and megachores each comprising combinations of the finer-scale classifications
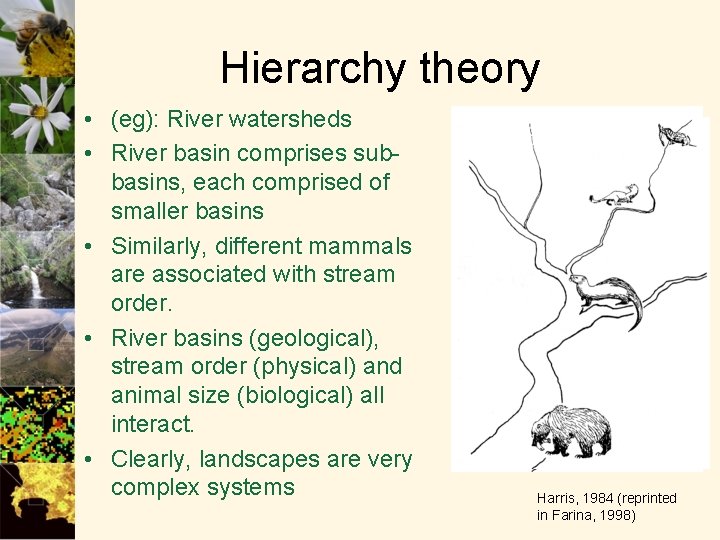
Hierarchy theory • (eg): River watersheds • River basin comprises subbasins, each comprised of smaller basins • Similarly, different mammals are associated with stream order. • River basins (geological), stream order (physical) and animal size (biological) all interact. • Clearly, landscapes are very complex systems Harris, 1984 (reprinted in Farina, 1998)

Hierarchy theory • To understand complex systems, one needs to focus on organizational level. • This means choosing a relevant spatiotemporal scale to study the system (hence the components of the system) • The horizontal structure of a hierarchical system comprises subsystems or holons • Each holon is an aggregate of lower-level holons, and is part of a higher one • The borders of a holon may be easily visible (the edge of a forest) or invisible (the edge of a frog’s distribution)

Hierarchy theory: holon borders • eg: the structure of a grassland (higher holon) depends on the processes of grazing and woodland encroachment acting on local scales • Finer-scale holons tend to have a faster behaviour rate than larger ones (grazing behaviour at a low level, • Outputs from one level to another are aggregates of the component processes • Consequently, holon levels and borders effectively act as filters for behaviour. Boundaries exist where there is a discontinuity in the rate of change of variables. • This is the basis of the hierarchical understanding of systems
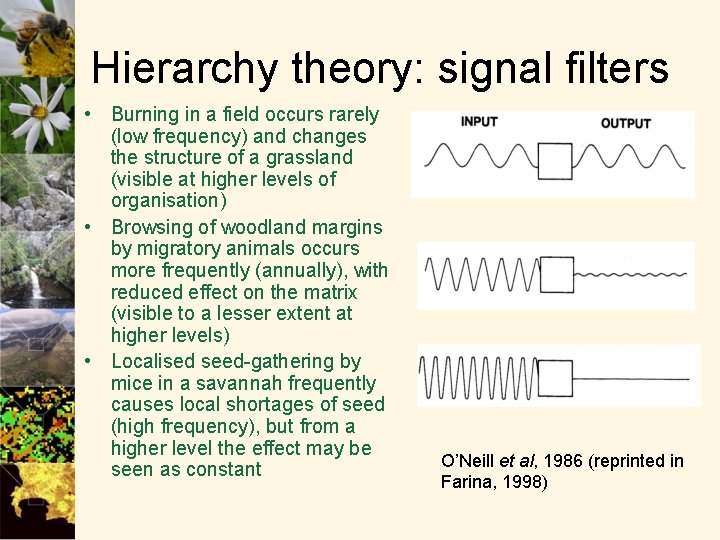
Hierarchy theory: signal filters • Burning in a field occurs rarely (low frequency) and changes the structure of a grassland (visible at higher levels of organisation) • Browsing of woodland margins by migratory animals occurs more frequently (annually), with reduced effect on the matrix (visible to a lesser extent at higher levels) • Localised seed-gathering by mice in a savannah frequently causes local shortages of seed (high frequency), but from a higher level the effect may be seen as constant O’Neill et al, 1986 (reprinted in Farina, 1998)

Hierarchy theory: Incorporation • Incorporation is the process by which perturbation is absorbed by a level of the system • Low frequency fires in a savannah tend to increase soil fertility, reduce woodland encroachment & provide high-quality fodder • Consequently, they increase biodiversity & complexity • Frequent (human-induced) fires can destroy the seed bank & reduce biodiversity, when the system can no longer incorporate the event • The system becomes less complex, turning from a woodland-grassland matrix to simple grassland, then to arid semi-desert.

Diffusion theory • • • This theory describes the movement of organisms through a Eqn (1) landscape. N=population size • Describes plants & f(N) = population growth animals, although function they obviously D = diffusion coefficient operate on different (describes spatial movement timescales rate) • The principle is = diffusion operator based on the (describes the rate of change diffusion of particles of N with distance – the in a liquid. density gradient) Turner et al, 2001

Diffusion theory • When invading a uniform landscape, landscape the rate of spread (V) will reach asymptotes equal to Eqn (2) where r is the intrinsic growth rate & D is the diffusion coefficient • Equation tested by Andow et al (1990), and was found to work well for – Invasion of muskrats in Europe – Invasion of cabbage white butterfly in North America • However, in the case of the cereal leaf beetle, movement patterns were considered on a finer scale, and it appeared that D was underestimated.

Percolation theory • Real landscapes are only uniform when considering very broad scales • At finer scales, percolation theory describes organismal movement through the matrix. • Differs from diffusion theory in that it considers the connectedness of the landscape • Also considers movement to be similar to a that of a fluid • Below a critical threshold (pc), distribution is patchy & separated into discrete regions • Above threshold, movement through the region is free • Experiments corroborate theory that the percolation critical threshold (pc) is <0. 5928
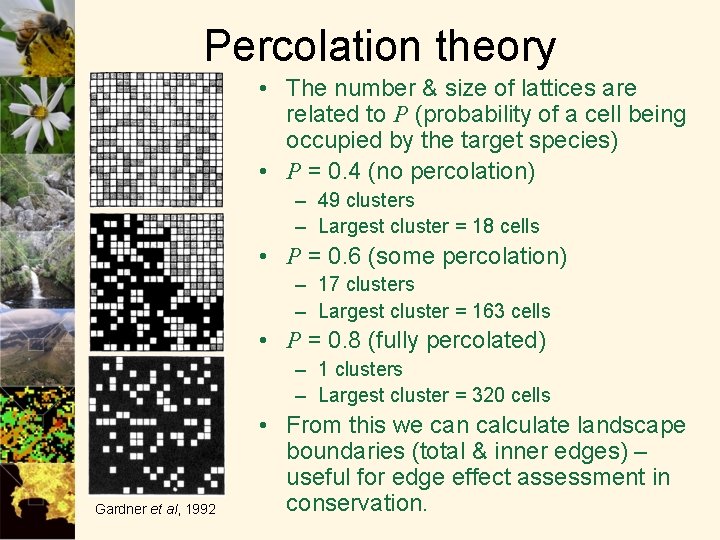
Percolation theory • The number & size of lattices are related to P (probability of a cell being occupied by the target species) • P = 0. 4 (no percolation) – 49 clusters – Largest cluster = 18 cells • P = 0. 6 (some percolation) – 17 clusters – Largest cluster = 163 cells • P = 0. 8 (fully percolated) – 1 clusters – Largest cluster = 320 cells Gardner et al, 1992 • From this we can calculate landscape boundaries (total & inner edges) – useful for edge effect assessment in conservation.

Percolation theory: uses • The occupancy can signify any resource, and we can thus estimate the likelihood of many events – resinous shrubs/trees: forest fires – carrier animals: disease spread – susceptible plants: pest outbreaks • Also useful for resource usage studies in animals • If a landscape has a percolation value over to pc (0. 5928), it can move throughout the landscape to find resources • Chance of finding no resources in n landscape units is Eqn (3) where P is the random distribution of the resource Farina, 1998

Percolation theory: uses • Therefore, the probability R or finding at least one resource is Eqn (4) • We know that if R=0. 5928 the animal can move through the landscape to find resources • Substituting this into equation 4 gives us the relationship between n and P : Eqn (5) • This then tells us far the animal needs to travel to obtain sufficient resources.

Percolation theory: resource use • Hence, when resources are well distributed (P<=pc), the organism doesn’t have to move very far • Decreasing resource density will require an organism to look further afield • When there are two or more available resources, n is calculated using their combined potential • If a dominant organism consumes 90% of a resource, the subdominant species has much lower resource availability, and must consequently search more land units • The likelihood of finding subdominant species in a given land unit is hence much smaller than for dominant species, even in relation to their densities (sample is insufficient) (O’Neill et al, 1988) • Furthermore, fragmented landscapes will reduce the viability of subdominant species first.

Summary • Hierarchy theory: all systems and processes in a landscape are components of higher-level systems • Incorporation: the extent to which perturbation can be absorbed by a system • Diffusion theory: in a homogeneous landscape, population dispersion is related to the population growth rate and the rate at which it can move • Percolation theory: in a fragmented landscape, movement rate is related to the integrity of the landscape. Over a critical threshold (pc = 0. 5928) organisms can move freely through the landscape. • Resource-gathering (& consequently home range) is related to resource density and landscape integrity

References • Andow, D. A. , Karieva, P. M. , Levin, S. A. & Okubo, A. (1990) Spread of invading organisms. Landscape Ecology 4: 177 -188. • Farina, A. (1998) Principles and Methods in Landscape Ecology. Chapman & Hall, London. • Harris, L. D. (1984) The fragmented forest. Island biography theory and the preservation of biotic diversity. University of Chicago Press, Chicago. • Gardner, R. H. , Turner, M. G. , Dale, V. H. & O’Neill, R. V. (1992) A percolation model of ecological flows. In: Hansen, A. J. & di Castri, F. (eds. ), Landscape boundaries. Consequences for biotic diversity and ecological flows. Springer-Verlag, New York, pp. 259 -269. • O’Neill, R. V. , De. Angelis, D. L. Waide, J. B. & Allen, T. F. H. (1986) a hierarchical concept of ecosystems. Princeton University Press, Princeton, New Jersey. • O’Neill, R. V. , Milne, B. T. , Turner, M. G. & Garnder, R. I. I. (1988) Resource utilization and landscape pattern. Landscape Ecology 2: 63 -69. • Turner, M. G. , Gardner, R. H. & O’Neill, R. V. (2001) Landscape Ecology in Theory and Practice: Pattern and Process. Springer. Verlag, New York 401 pp.
- Slides: 18