BBY 428 Metin Analitii Prof Dr Tlay Ouz

BBY 428 Metin Analitiği Prof. Dr. Tülay Oğuz

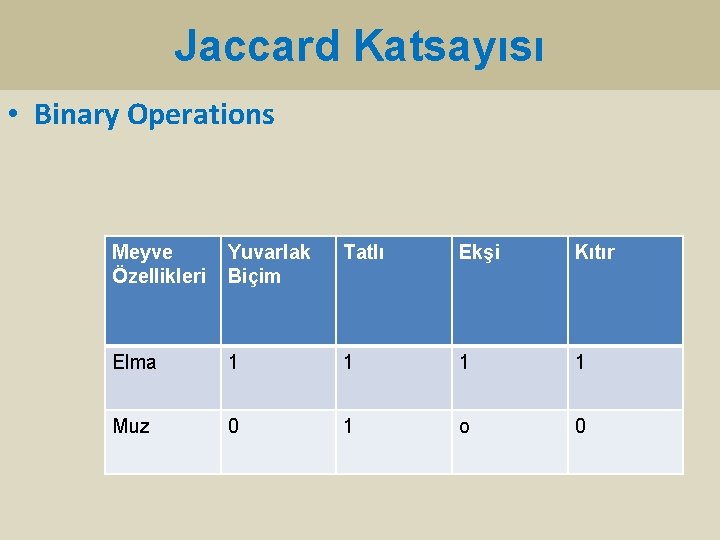
Jaccard Katsayısı • Binary Operations Meyve Özellikleri Yuvarlak Biçim Tatlı Ekşi Kıtır Elma 1 1 Muz 0 1 o 0

Jaccard Katsayısı • P/p+q+r • p: ortak eleman sayısı • q: A kümesinde olup B’de olmayan eleman sayısı • r: B’de olup A’da olmayan eleman sayısı • Elma (1111) p: 1 1 / 1+3+0 = 1 / 4 = 0, 25 • Muz (0100) q: 3 r: 0

Jaccard Katsayısı • D 1 = (I, Ş, I, L) D 2 = (S, E, L, E, N) D 3 = (Ç, A, Ğ, L, A) D 4 = (R, A, B, İ, A) A 4 L 3 E 2 I 2 Ş 1 S 1 N 1 Ç 1 Toplam Frekanslar Ğ 1 R 1 B 1 İ 1

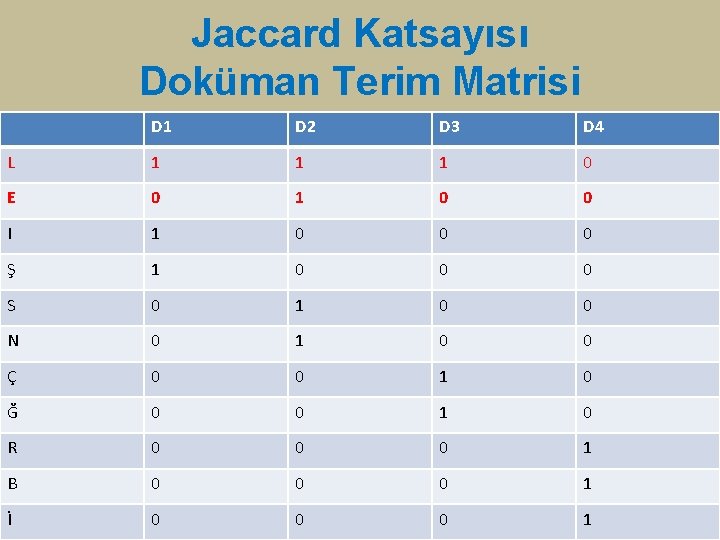
Jaccard Katsayısı Doküman Terim Matrisi D 1 D 2 D 3 D 4 L 1 1 1 0 E 0 1 0 0 I 1 0 0 0 Ş 1 0 0 0 S 0 1 0 0 N 0 1 0 0 Ç 0 0 1 0 Ğ 0 0 1 0 R 0 0 0 1 B 0 0 0 1 İ 0 0 0 1

Jaccard Katsayısı Set Operations Binary Operations • • • Sorgu: {L, E} S = (1, 1, 0, 0, 0) D 1: {L, I, Ş} D 1= (1, 0, 1, 1, 0, 0, 0, 0) D 2: {L, E, S, N} D 2= (1, 1, 0, 0, 0) D 3: {L, Ç, Ğ} D 3= (1, 0, 0, 0, 1, 1, 0, 0, 0) D 4: {R, B, İ} D 4= (0, 0, 1, 1, 1) JK(D 1, S)= ḷD 1 ∩ S ḷ / ḷ D 1 U S ḷ =1/4=0, 25 JK(D 2, S)= ḷD 2 ∩ S ḷ / ḷ D 2 U S ḷ =2/4=0, 50 JK(D 3, S)= ḷ D 3 ∩ S ḷ / ḷ D 3 U S ḷ =1/4=0, 25 JK(D 4, S)= ḷ D 4 ∩ S ḷ / ḷ D 4 U S ḷ =0/5=0

Jaccard Katsayısı • • • JK(D 1, S)= 1/ 1+1+2=1/4=0, 25 JK(D 2, S)= 2/2+0+2=2/4=0, 50 JK(D 3, S)= 1/1+1+2=1/4=0, 25 JK(D 4, S)= 0 Jaccard benzerlik ölçümü sıralı erişimde kullanılır. Benzerlik katsayılarına göre en ilgiliden en ilgisize doğru bizi dokümanlara eriştirir.

Boolean Modeline Göre Erişim • Boolean Modele Göre Erişim • L = (1110) AND • E = (0100) • = (0100) =D 2 • Burada yalnız eriştiğimiz dokümanı görebiliriz. Sıralı bir erişim vermez.

Dice Katsayısı • Dice katsayısı iki kümenin benzerliğini ölçer. Aynı zamanda iki söz dizisinin ortak bigram sayısı cinsinden benzerlik ölçümünde de kullanılır. (bir bigram bir söz dizisindeki komşu harf çiftidir) • Dice benzerlik ölçümünün kullanıldığı alanlardan biri, web siteleridir. Site içinde gezinen kullanıcıların inceledikleri birimlerle benzerlik gösteren diğer birimleri onlara sunabilmek için kullanılır.

Dice Katsayısı • Amazon. com buna örnek gösterilebilir. Kullanıcının arama geçmişine bakarak bir öneriler listesi kullanıcıya sunulur. • Örneğin bir müzik sitesinde gezinen ve Pink Floyd’un “dark side of the moon” albümüne bakan bir kullanıcıya, benzer albümlere de bakması için bir liste sunulabilir. Kullanıcının, grubun diğer albümü “wish you were here” veya Led Zepplin’in meddle albümüne de bakması önerilebilir.

Dice Katsayısı • İki birim arasındaki benzerlik ölçülürken birimleri tanımlayan özelliklere bakılır. • Hangi birimlerin benzer olduğunu bulabilmek için onları skorlandırmak gerekir. • En yüksek skora sahip olan, en benzer olandır. • Tanımlayıcı özellikler web 2. 0 dilinde aslında etiketlerdir. • X ve Y gibi iki farklı birimin etiket listeleri Tx ve Ty olarak gösterildiğinde

Dice Katsayısı • X ve Y arasındaki benzerliği hesaplamanın basit bir yolu, her iki birimde ortak olan etiket sayısını bulmaktır. • Böylelikle X ve Y arasındaki benzerlik skoru, Ben(X, Y) = |{Tx} ∩ {Ty}| • X=”Dark Side of the Moon”, • {Tx} = {“müzik”, “rock”, “pink floyd”, “cult”} • Y="Meddle", • (Ty} = {"müzik", "led zeppelin", "cult", "rock“}

Dice Katsayısı • Dermedeki bütün birimlerin benzerliğini aynı biçimde hesaplayabilir ve verili birimle benzerliği olan Top-K sonucu gösterebiliriz. Genelde en iyi 10 benzer birim gösterilir. • Sorun: • A-Etiket sayısı fazla olan birimler, daha fazla ortak eleman üretir. Büyük kümeler, uzun dokümanlar • B-İki birimin benzerlik skoru arasında korelasyon yoktur.

Dice Katsayısı • A-Eşik değer belirleyemeyiz. Örn: En benzer top-k dokümanı getirecek bir sınırlama getiremeyiz. • B-Çapraz benzerlik analizi yapamayız. Örn: A, B benzerliğinin C, D benzerliğinden fazla olduğunu söyleyemez. • Benzerliği bulmanın daha iyi bir yolu, benzerlik skorunda uzunluğunu normalize etmektir

Dice Katsayısı • Burada • a) skor, daha fazla etiketi olan dokümanların etkisinde kalmaz ve • b) benzerlik skoru her zaman 1 ve 0 arasında olur. • Böylelikle istendiğinde bir eşik değer belirlenebilir. • Peki skorları nasıl normalize edeceğiz?

Dice Katsayısı • Ben(X, Y) = (2*|Tx ∩ Ty|) / (|Tx|+|Ty|) • Dice katsayısı denir. İki küme arasındaki benzerliği ölçmede kullanılır • Top-K dokümanı depolarken, bütün benzer dokümanları depolayıp sonra benzer top-k dokümanı içinden çekip almak yerine heap yapısını kullanmak daha iyidir.

Cosine Benzerlik Ölçümü • │A B│/ │A│* │B│ set operations • (A, B) = A*B / A 2*B 2 uzunluğu normalize edilmiş vektör çarpımı

Cosine Benzerlik Ölçümü • • • Sorgu: {L, E} S = (1, 1, 0, 0, 0) D 1: {L, I, Ş} D 1= (1, 0, 1, 1, 0, 0, 0, 0) D 2: {L, E, S, N} D 2= (1, 1, 0, 0, 0) D 3: {L, Ç, Ğ} D 3= (1, 0, 0, 0, 1, 1, 0, 0, 0) D 4: {R, B, İ} D 4= (0, 0, 1, 1, 1) COS(D 1, S)= 1 / 2*3 = 1/ 2, 44 = 0, 40 COS(D 2, S)= 2/ 2*4= 2/ 2, 82 = 0, 70 COS(D 3, S)= 0, 40 COS(D 4, S)=0

Yararlı Linkler • Term-Document Incidence Matrices http: //www. youtube. com/watch? v=ftd. IIX 5 SM 0&NR=1&feature=endscreen • Introducing Ranked Retrieval • http: //www. youtube. com/watch? v=5 Gz 3 Hp 217 Io • Scoring with the Jaccard Coefficient http: //www. youtube. com/watch? v=Vbdki_gnn. Y M