Bayesian Statistics and Belief Networks Overview Book Ch

Bayesian Statistics and Belief Networks

Overview • • Book: Ch 8. 3 Refresher on Bayesian statistics Bayesian classifiers Belief Networks / Bayesian Networks

Why Should We Care? • Theoretical framework for machine learning, classification, knowledge representation, analysis • Bayesian methods are capable of handling noisy, incomplete data sets • Bayesian methods are commonly in use today

Bayesian Approach To Probability and Statistics • Classical Probability : Physical property of the world (e. g. , 50% flip of a fair coin). True probability. • Bayesian Probability : A person’s degree of belief in event X. Personal probability. • Unlike classical probability, Bayesian probabilities benefit from but do not require repeated trials only focus on next event; e. g. probability Seawolves win next game?

Bayes Rule Product Rule: Equating Sides: i. e. All classification methods can be seen as estimates of Bayes’ Rule, with different techniques to estimate P(evidence|Class).

Simple Bayes Rule Example Probability your computer has a virus, V, = 1/1000. If virused, the probability of a crash that day, C, = 4/5. Probability your computer crashes in one day, C, = 1/10. P(C|V)=0. 8 P(V)=1/1000 P(C)=1/10 Even though a crash is a strong indicator of a virus, we expect only 8/1000 crashes to be caused by viruses. Why not compute P(V|C) from direct evidence? Causal vs. Diagnostic knowledge; (consider if P(C) suddenly drops).

Bayesian Classifiers If we’re selecting the single most likely class, we only need to find the class that maximizes P(e|Class)P(Class). Hard part is estimating P(e|Class). Evidence e typically consists of a set of observations: Usual simplifying assumption is conditional independence:

Bayesian Classifier Example Probability P(C) P(crashes|C) P(diskfull|C) C=Virus 0. 4 0. 1 0. 6 C=Bad Disk 0. 6 0. 2 0. 1 Given a case where the disk is full and computer crashes, the classifier chooses Virus as most likely since (0. 4)(0. 1)(0. 6) > (0. 6)(0. 2)(0. 1).

Beyond Conditional Independence Linear Classifier: C 1 C 2 • Include second-order dependencies; i. e. pairwise combination of variables via joint probabilities: Correction factor Difficult to compute - joint probabilities to consider

Belief Networks • DAG that represents the dependencies between variables and specifies the joint probability distribution • Random variables make up the nodes • Directed links represent causal direct influences • Each node has a conditional probability table quantifying the effects from the parents • No directed cycles
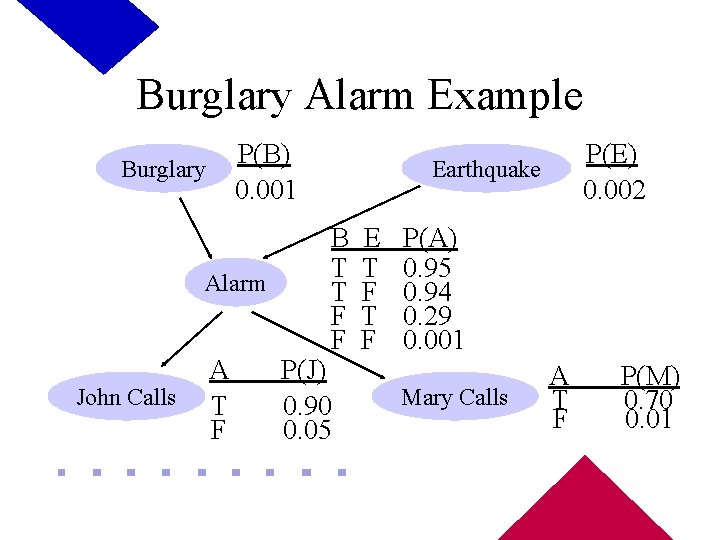
Burglary Alarm Example P(B) 0. 001 Burglary Alarm John Calls A T F P(E) 0. 002 Earthquake B T T F F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls A T F P(M) 0. 70 0. 01
Sample Bayesian Network

Using The Belief Network Burglary P(B) 0. 001 Earthquake B T T F F Alarm John Calls A T F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls P(E) 0. 002 A T F P(M) 0. 70 0. 01 Probability of alarm, no burglary or earthquake, both John and Mary call:

Belief Computations • Two types; both are NP-Hard • Belief Revision – Model explanatory/diagnostic tasks – Given evidence, what is the most likely hypothesis to explain the evidence? – Also called abductive reasoning • Belief Updating – Queries – Given evidence, what is the probability of some other random variable occurring?

Belief Revision • Given some evidence variables, find the state of all other variables that maximize the probability. • E. g. : We know John Calls, but not Mary. What is the most likely state? Only consider assignments where J=T and M=F, and maximize. Best:

Belief Updating • Causal Inferences E Q • Diagnostic Inferences Q E • Intercausal Inferences Q E • Mixed Inferences E Q E
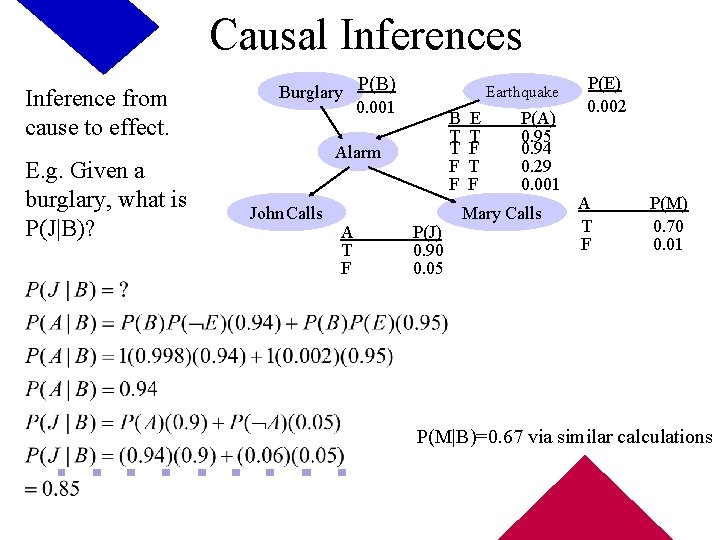
Causal Inferences Inference from cause to effect. E. g. Given a burglary, what is P(J|B)? Burglary P(B) 0. 001 Earthquake B T T F F Alarm John Calls A T F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls P(E) 0. 002 A T F P(M) 0. 70 0. 01 P(M|B)=0. 67 via similar calculations

Diagnostic Inferences From effect to cause. E. g. Given that John calls, what is the P(burglary)? What is P(J)? Need P(A) first: Many false positives.

Intercausal Inferences Explaining Away Inferences. Given an alarm, P(B|A)=0. 37. But if we add the evidence that earthquake is true, then P(B|A^E)=0. 003. Even though B and E are independent, the presence of one may make the other more/less likely.

Mixed Inferences Simultaneous intercausal and diagnostic inference. E. g. , if John calls and Earthquake is false: Computing these values exactly is somewhat complicated.

Exact Computation Polytree Algorithm • Judea Pearl, 1982 • Only works on singly-connected networks - at most one undirected path between any two nodes. • Backward-chaining Message-passing algorithm for computing posterior probabilities for query node X – Compute causal support for X, evidence variables “above” X – Compute evidential support for X, evidence variables “below” X
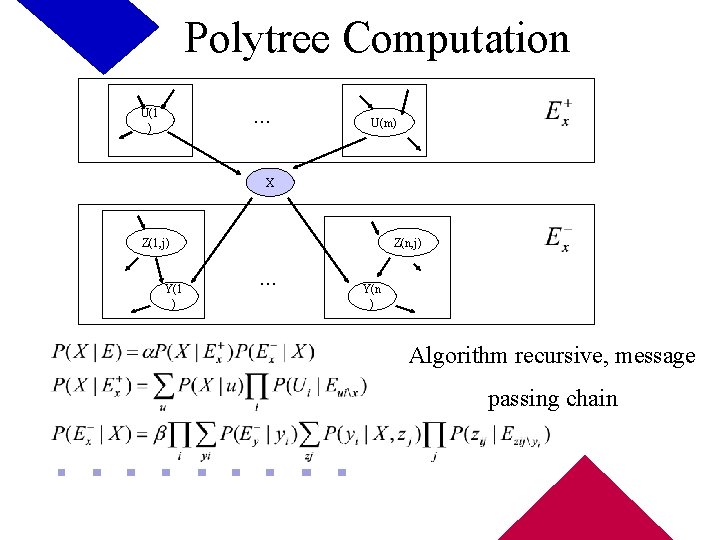
Polytree Computation. . . U(1 ) U(m) X Z(1, j) Y(1 ) Z(n, j) . . . Y(n ) Algorithm recursive, message passing chain

Other Query Methods • Exact Algorithms – Clustering • Cluster nodes to make single cluster, message-pass along that cluster – Symbolic Probabilistic Inference • Uses d-separation to find expressions to combine • Approximate Algorithms – Select sampling distribution, conduct trials sampling from root to evidence nodes, accumulating weight for each node. Still tractable for dense networks. • Forward Simulation • Stochastic Simulation

Summary • Bayesian methods provide sound theory and framework for implementation of classifiers • Bayesian networks a natural way to represent conditional independence information. Qualitative info in links, quantitative in tables. • NP-complete or NP-hard to compute exact values; typical to make simplifying assumptions or approximate methods. • Many Bayesian tools and systems exist

References • Russel, S. and Norvig, P. (1995). Artificial Intelligence, A Modern Approach. Prentice Hall. • Weiss, S. and Kulikowski, C. (1991). Computer Systems That Learn. Morgan Kaufman. • Heckerman, D. (1996). A Tutorial on Learning with Bayesian Networks. Microsoft Technical Report MSR-TR -95 -06. • Internet Resources on Bayesian Networks and Machine Learning: http: //www. cs. orst. edu/~wangxi/resource. html
- Slides: 25