Bayesian Statistics and Belief Networks Overview Book Ch

Bayesian Statistics and Belief Networks

Overview • • Book: Ch 13, 14 Refresher on Probability Bayesian classifiers Belief Networks / Bayesian Networks

Why Should We Care? • Theoretical framework for machine learning, classification, knowledge representation, analysis • Bayesian methods are capable of handling noisy, incomplete data sets • Bayesian methods are commonly in use today

Bayesian Approach To Probability and Statistics • Classical Probability : Physical property of the world (e. g. , 50% flip of a fair coin). True probability. • Bayesian Probability : A person’s degree of belief in event X. Personal probability. • Unlike classical probability, Bayesian probabilities benefit from but do not require repeated trials only focus on next event; e. g. probability Seawolves win next game?

Uncertainty

Methods for Handling Uncertainty

Probability

Making Decisions Under Uncertainty

Probability Basics

Random Variables

Prior Probability

Conditional Probability
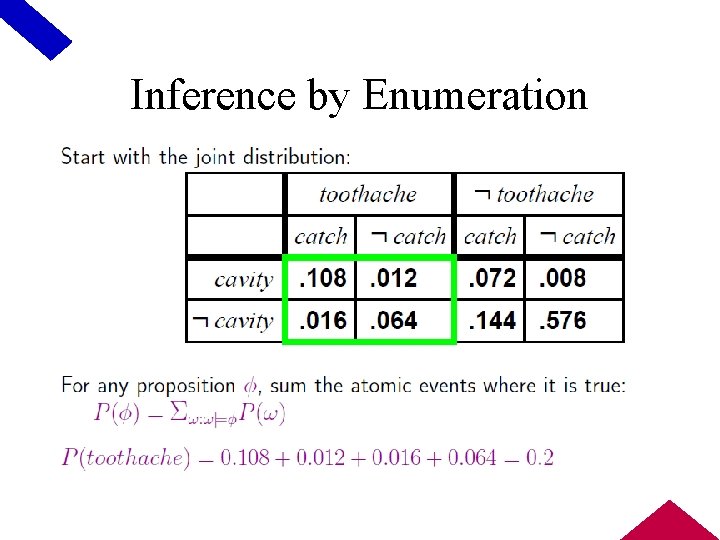
Inference by Enumeration

Inference by Enumeration

Bayes Rule Product Rule: Equating Sides: i. e. All classification methods can be seen as estimates of Bayes’ Rule, with different techniques to estimate P(evidence|Class).

Inference by Enumeration

Simple Bayes Rule Example Probability your computer has a virus, V, = 1/1000. If virused, the probability of a crash that day, C, = 4/5. Probability your computer crashes in one day, C, = 1/10. P(C|V)=0. 8 P(V)=1/1000 P(C)=1/10 Even though a crash is a strong indicator of a virus, we expect only 8/1000 crashes to be caused by viruses. Why not compute P(V|C) from direct evidence? Causal vs. Diagnostic knowledge; (consider if P(C) suddenly drops).

Bayesian Classifiers If we’re selecting the single most likely class, we only need to find the class that maximizes P(e|Class)P(Class). Hard part is estimating P(e|Class). Evidence e typically consists of a set of observations: Usual simplifying assumption is conditional independence:

Bayesian Classifier Example Probability P(C) P(crashes|C) P(diskfull|C) C=Virus 0. 4 0. 1 0. 6 C=Bad Disk 0. 6 0. 2 0. 1 Given a case where the disk is full and computer crashes, the classifier chooses Virus as most likely since (0. 4)(0. 1)(0. 6) > (0. 6)(0. 2)(0. 1).

Beyond Conditional Independence Linear Classifier: C 1 C 2 • Include second-order dependencies; i. e. pairwise combination of variables via joint probabilities: Correction factor Difficult to compute - joint probabilities to consider

Belief Networks • DAG that represents the dependencies between variables and specifies the joint probability distribution • Random variables make up the nodes • Directed links represent causal direct influences • Each node has a conditional probability table quantifying the effects from the parents • No directed cycles

Burglary Alarm Example P(B) 0. 001 Burglary Alarm John Calls A T F P(E) 0. 002 Earthquake B T T F F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls A T F P(M) 0. 70 0. 01
Sample Bayesian Network

Using The Belief Network Burglary P(B) 0. 001 Earthquake B T T F F Alarm John Calls A T F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls P(E) 0. 002 A T F P(M) 0. 70 0. 01 Probability of alarm, no burglary or earthquake, both John and Mary call:

Belief Computations • Two types; both are NP-Hard • Belief Revision – Model explanatory/diagnostic tasks – Given evidence, what is the most likely hypothesis to explain the evidence? – Also called abductive reasoning • Belief Updating – Queries – Given evidence, what is the probability of some other random variable occurring?

Belief Revision • Given some evidence variables, find the state of all other variables that maximize the probability. • E. g. : We know John Calls, but not Mary. What is the most likely state? Only consider assignments where J=T and M=F, and maximize. Best:

Belief Updating • Causal Inferences E Q • Diagnostic Inferences Q E • Intercausal Inferences Q E • Mixed Inferences E Q E
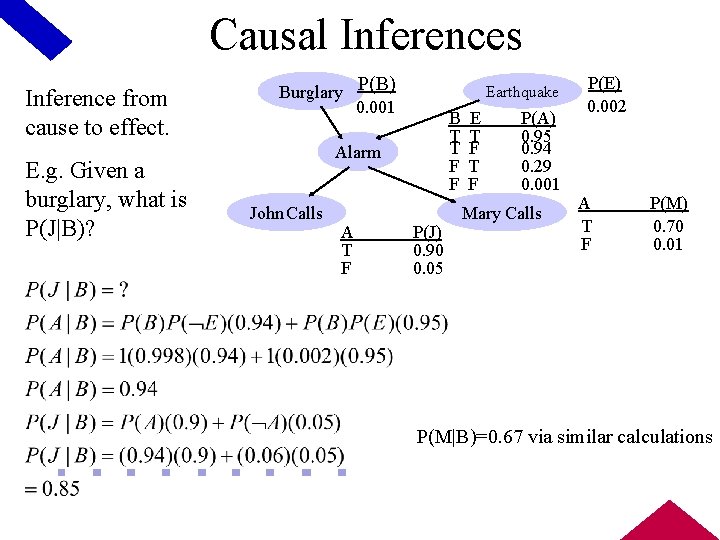
Causal Inferences Inference from cause to effect. E. g. Given a burglary, what is P(J|B)? Burglary P(B) 0. 001 Earthquake B T T F F Alarm John Calls A T F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls P(E) 0. 002 A T F P(M) 0. 70 0. 01 P(M|B)=0. 67 via similar calculations

Diagnostic Inferences From effect to cause. E. g. Given that John calls, what is the P(burglary)? What is P(J)? Need P(A) first: Many false positives.

Intercausal Inferences Explaining Away Inferences. Given an alarm, P(B|A)=0. 37. But if we add the evidence that earthquake is true, then P(B|A^E)=0. 003. Even though B and E are independent, the presence of one may make the other more/less likely.

Mixed Inferences Simultaneous intercausal and diagnostic inference. E. g. , if John calls and Earthquake is false: Computing these values exactly is somewhat complicated.

Exact Computation Polytree Algorithm • Judea Pearl, 1982 • Only works on singly-connected networks - at most one undirected path between any two nodes. • Backward-chaining Message-passing algorithm for computing posterior probabilities for query node X – Compute causal support for X, evidence variables “above” X – Compute evidential support for X, evidence variables “below” X
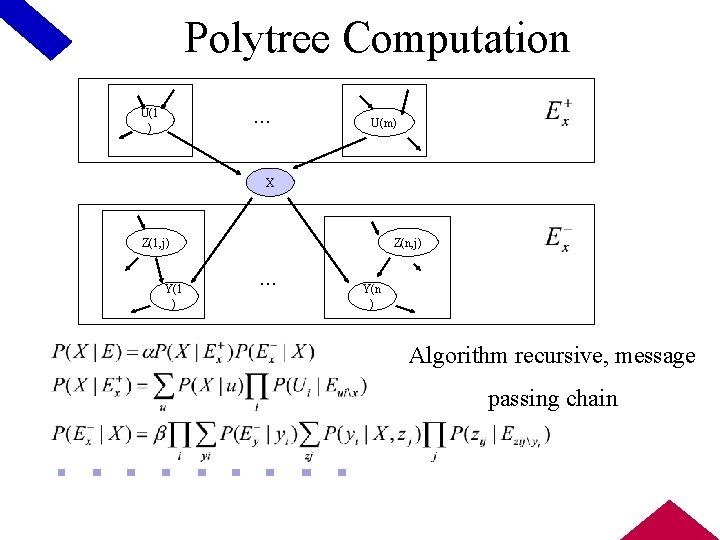
Polytree Computation. . . U(1 ) U(m) X Z(1, j) Y(1 ) Z(n, j) . . . Y(n ) Algorithm recursive, message passing chain

Other Query Methods • Exact Algorithms – Clustering • Cluster nodes to make single cluster, message-pass along that cluster – Symbolic Probabilistic Inference • Uses d-separation to find expressions to combine • Approximate Algorithms – Select sampling distribution, conduct trials sampling from root to evidence nodes, accumulating weight for each node. Still tractable for dense networks. • Forward Simulation • Stochastic Simulation

Summary • Bayesian methods provide sound theory and framework for implementation of classifiers • Bayesian networks a natural way to represent conditional independence information. Qualitative info in links, quantitative in tables. • NP-complete or NP-hard to compute exact values; typical to make simplifying assumptions or approximate methods. • Many Bayesian tools and systems exist

References • Russel, S. and Norvig, P. (1995). Artificial Intelligence, A Modern Approach. Prentice Hall. • Weiss, S. and Kulikowski, C. (1991). Computer Systems That Learn. Morgan Kaufman. • Heckerman, D. (1996). A Tutorial on Learning with Bayesian Networks. Microsoft Technical Report MSR-TR -95 -06. • Internet Resources on Bayesian Networks and Machine Learning: http: //www. cs. orst. edu/~wangxi/resource. html
- Slides: 36