BAYESIAN NETWORKS SOME APPLICATIONS OF BN Medical diagnosis

BAYESIAN NETWORKS

SOME APPLICATIONS OF BN Medical diagnosis Troubleshooting of hardware/software systems Fraud/uncollectible debt detection Data mining Analysis of genetic sequences Data interpretation, computer vision, image understanding
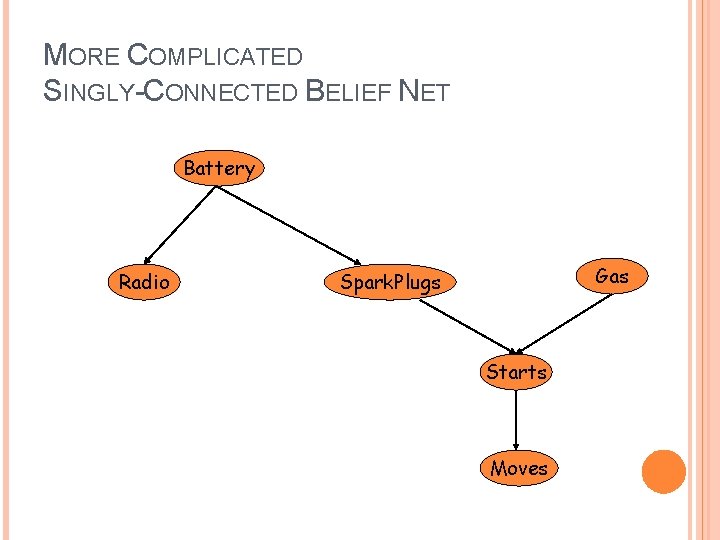
MORE COMPLICATED SINGLY-CONNECTED BELIEF NET Battery Radio Gas Spark. Plugs Starts Moves
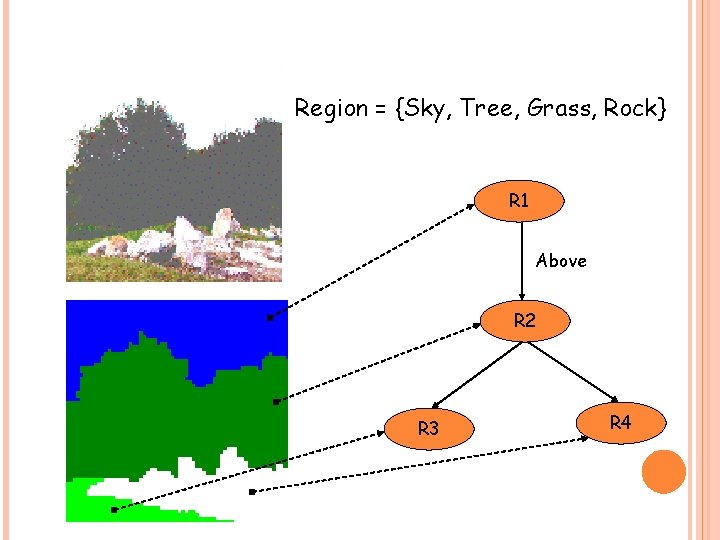
Region = {Sky, Tree, Grass, Rock} R 1 Above R 2 R 3 R 4
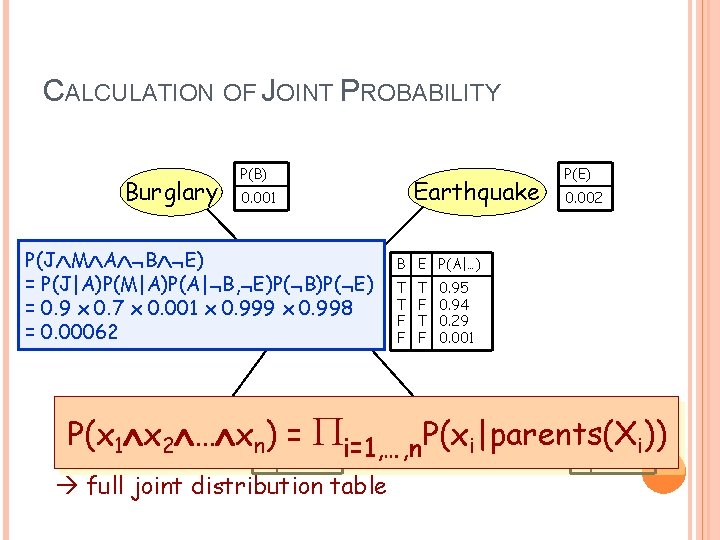
CALCULATION OF JOINT PROBABILITY Burglary P(B) Earthquake 0. 001 P(J M A B E) = P(J|A)P(M|A)P(A| B, E)P( B)P( E) Alarm = 0. 9 x 0. 7 x 0. 001 x 0. 999 x 0. 998 = 0. 00062 P(E) 0. 002 B E P(A|…) T T F F T F 0. 95 0. 94 0. 29 0. 001 P(x 1 x = Pi=1, …, n. P(x John. Calls Mary. Calls T 0. 70 i)) 2 … xn. T) 0. 90 i|parents(X A P(J|…) A P(M|…) F 0. 05 F 0. 01 full joint distribution table
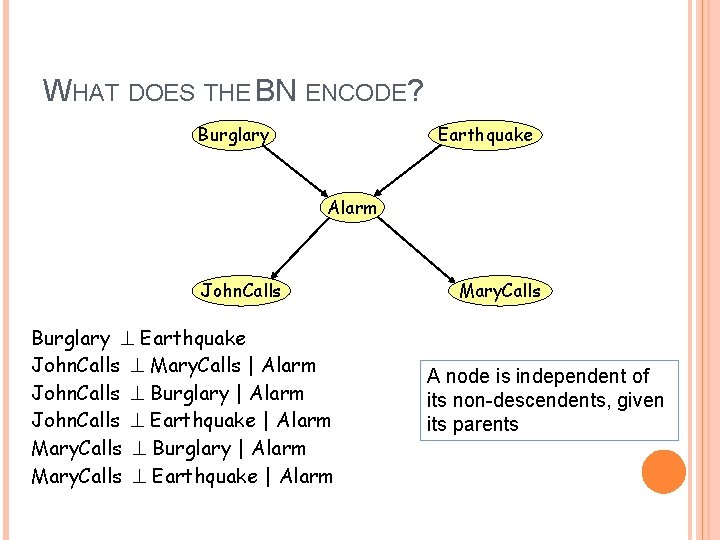
WHAT DOES THE BN ENCODE? Burglary Earthquake Alarm John. Calls Burglary Earthquake John. Calls Mary. Calls | Alarm John. Calls Burglary | Alarm John. Calls Earthquake | Alarm Mary. Calls Burglary | Alarm Mary. Calls Earthquake | Alarm Mary. Calls A node is independent of its non-descendents, given its parents

PROBABILISTIC INFERENCE Is the following problem…. Given: �A belief state P(X 1, …, Xn) in some form (e. g. , a Bayes net or a joint probability table) � A query variable indexed by q � Some subset of evidence variables indexed by e 1, …, ek Find: � P(Xq | Xe 1 , …, Xek)
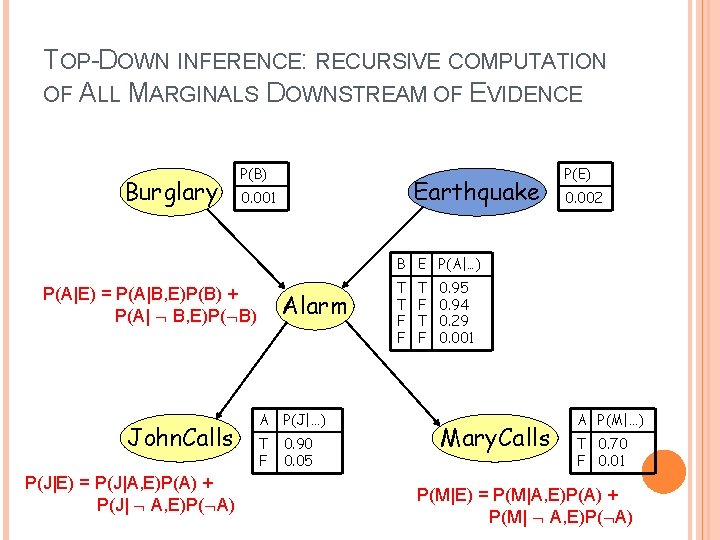
TOP-DOWN INFERENCE: RECURSIVE COMPUTATION OF ALL MARGINALS DOWNSTREAM OF EVIDENCE Burglary P(B) Earthquake 0. 001 P(E) 0. 002 B E P(A|…) P(A|E) = P(A|B, E)P(B) + P(A| B, E)P( B) John. Calls P(J|E) = P(J|A, E)P(A) + P(J| A, E)P( A) Alarm A P(J|…) T F 0. 90 0. 05 T T F F T F 0. 95 0. 94 0. 29 0. 001 Mary. Calls A P(M|…) T 0. 70 F 0. 01 P(M|E) = P(M|A, E)P(A) + P(M| A, E)P( A)

TOP-DOWN INFERENCE Only works if the graph of ancestors of a variable is a polytree Evidence given on ancestor(s) of the query variable Efficient: � O(d 2 k) time, where d is the number of ancestors of a variable, with k a bound on # of parents � Evidence on an ancestor cuts off influence of portion of graph above evidence node
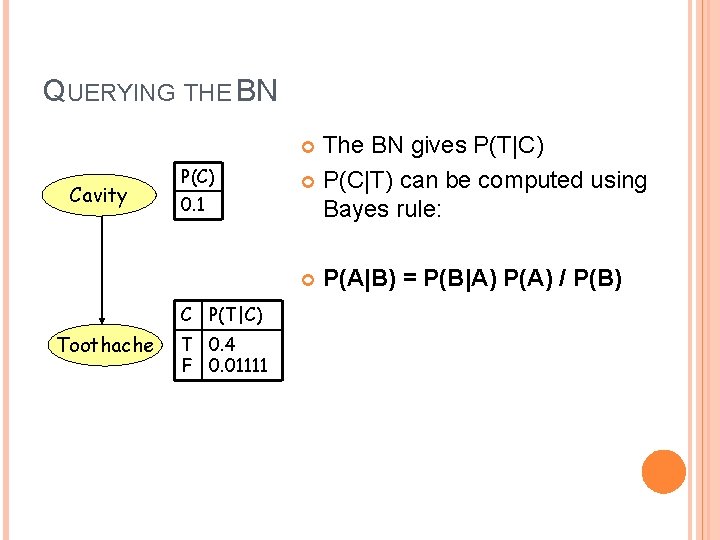
QUERYING THE BN The BN gives P(T|C) P(C|T) can be computed using Bayes rule: Cavity P(C) 0. 1 C P(T|C) Toothache T 0. 4 F 0. 01111 P(A|B) = P(B|A) P(A) / P(B)
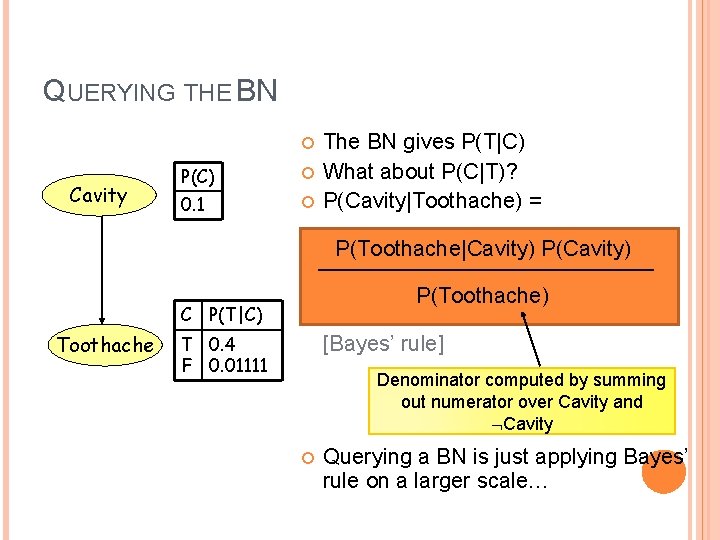
QUERYING THE BN Cavity P(C) 0. 1 The BN gives P(T|C) What about P(C|T)? P(Cavity|Toothache) = P(Toothache|Cavity) P(Toothache) C P(T|C) Toothache T 0. 4 F 0. 01111 [Bayes’ rule] Denominator computed by summing out numerator over Cavity and Cavity Querying a BN is just applying Bayes’ rule on a larger scale…
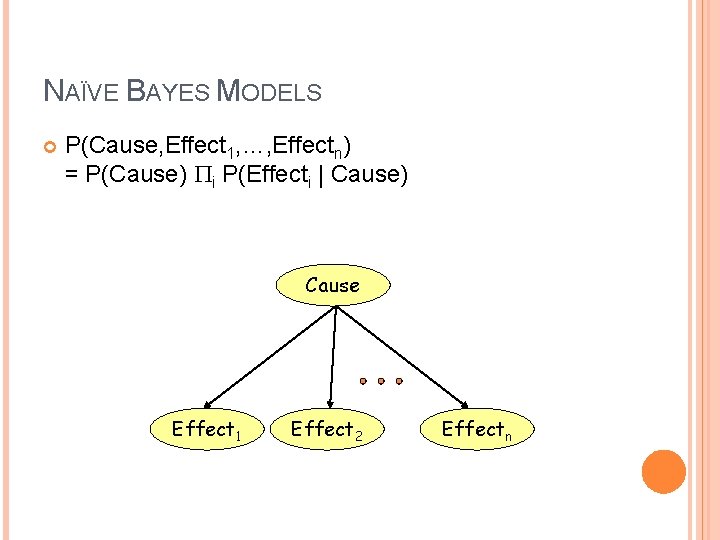
NAÏVE BAYES MODELS P(Cause, Effect 1, …, Effectn) = P(Cause) Pi P(Effecti | Cause) Cause Effect 1 Effect 2 Effectn
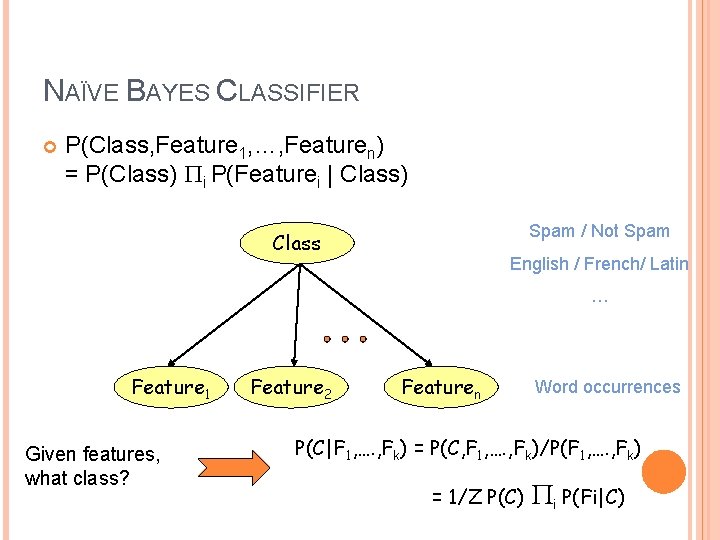
NAÏVE BAYES CLASSIFIER P(Class, Feature 1, …, Featuren) = P(Class) Pi P(Featurei | Class) Spam / Not Spam Class English / French/ Latin … Feature 1 Given features, what class? Feature 2 Featuren Word occurrences P(C|F 1, …. , Fk) = P(C, F 1, …. , Fk)/P(F 1, …. , Fk) = 1/Z P(C) Pi P(Fi|C)

COMMENTS ON NAÏVE BAYES MODELS Very scalable (thousands or millions of features!), easy to implement Easily handles missing data: just ignore the feature Conditional independence of features is main weakness. What if two features were actually correlated? Many features?
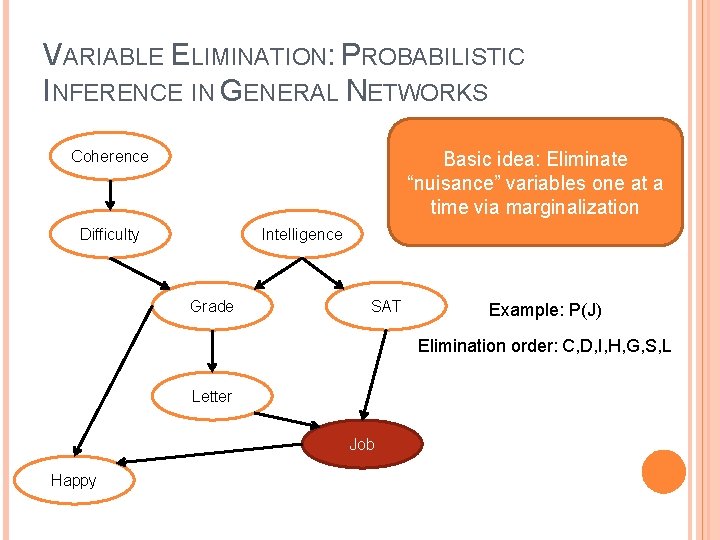
VARIABLE ELIMINATION: PROBABILISTIC INFERENCE IN GENERAL NETWORKS Coherence Basic idea: Eliminate “nuisance” variables one at a time via marginalization Difficulty Intelligence Grade SAT Example: P(J) Elimination order: C, D, I, H, G, S, L Letter Job Happy
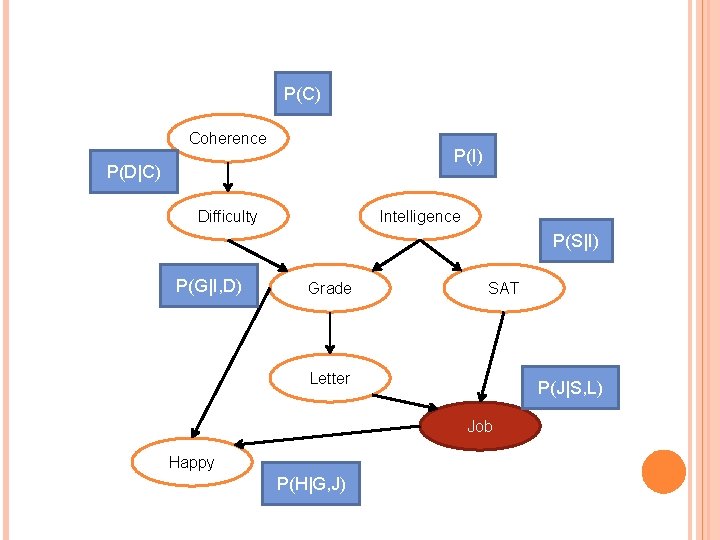
P(C) Coherence P(I) P(D|C) Difficulty Intelligence P(S|I) P(G|I, D) Grade SAT Letter P(J|S, L) Job Happy P(H|G, J)
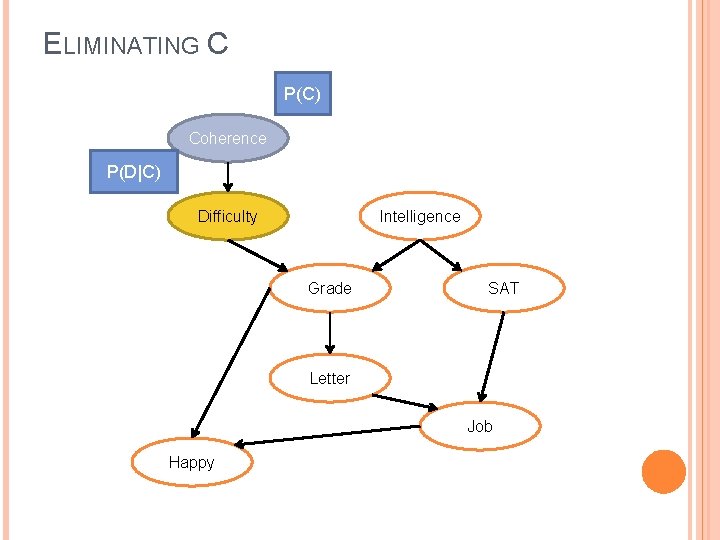
ELIMINATING C P(C) Coherence P(D|C) Difficulty Intelligence Grade SAT Letter Job Happy
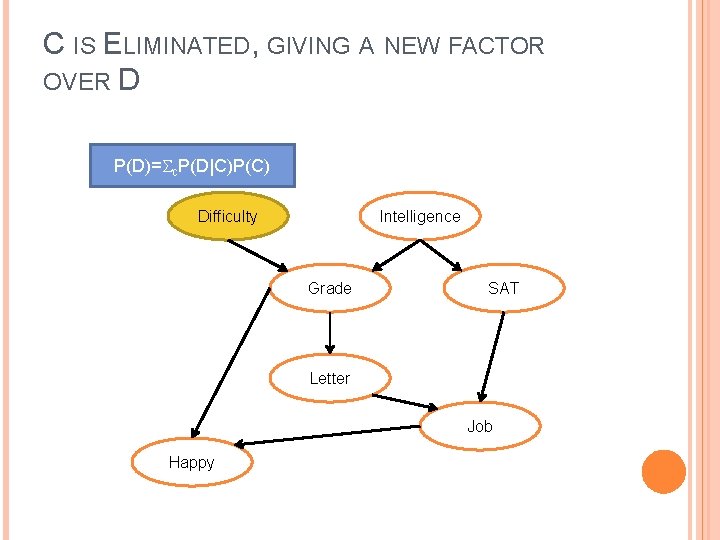
C IS ELIMINATED, GIVING A NEW FACTOR OVER D P(D)= c. P(D|C)P(C) Difficulty Intelligence Grade SAT Letter Job Happy
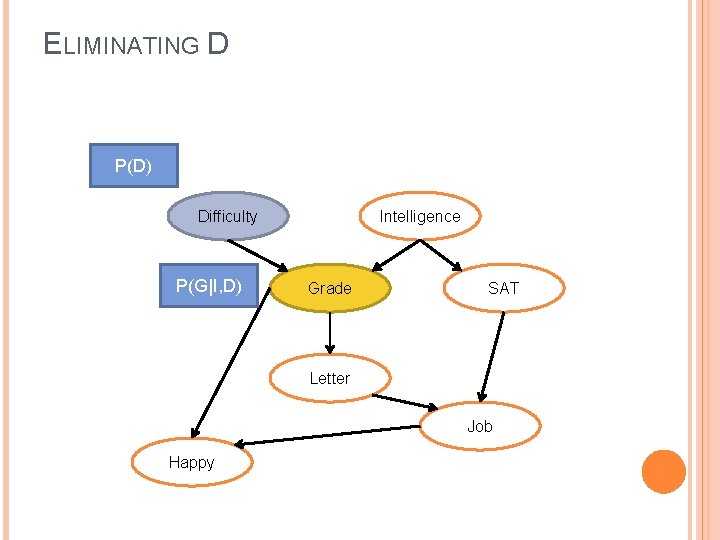
ELIMINATING D P(D) Difficulty P(G|I, D) Intelligence Grade SAT Letter Job Happy
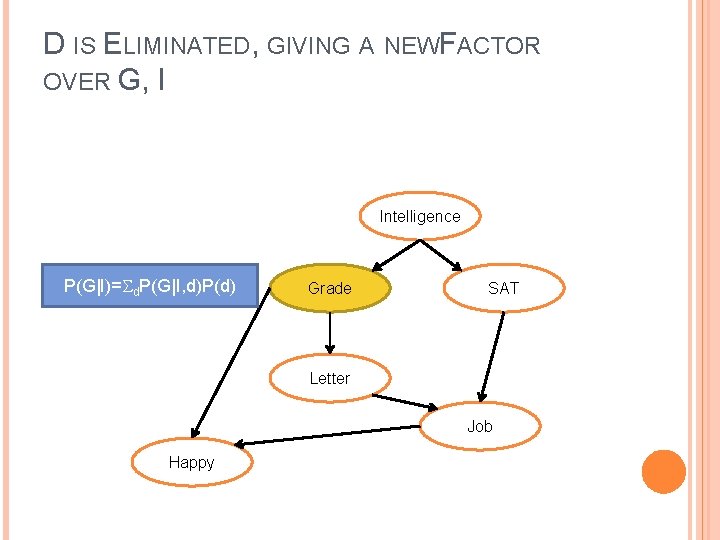
D IS ELIMINATED, GIVING A NEWFACTOR OVER G, I Intelligence P(G|I)= d. P(G|I, d)P(d) Grade SAT Letter Job Happy
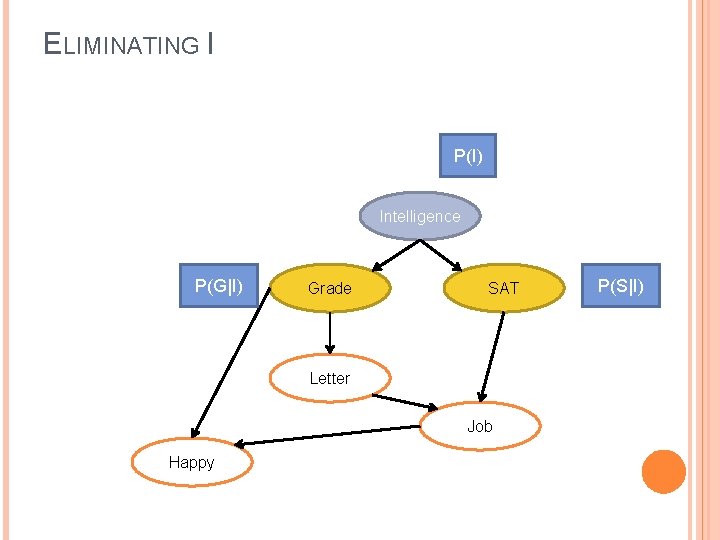
ELIMINATING I P(I) Intelligence P(G|I) Grade SAT Letter Job Happy P(S|I)
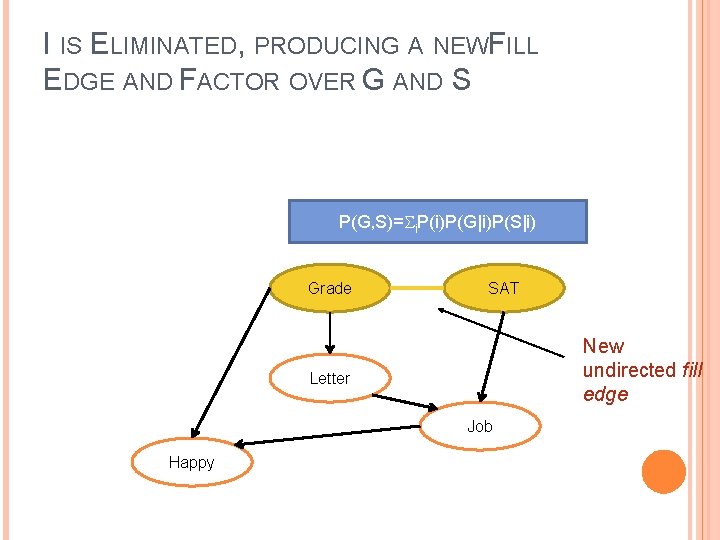
I IS ELIMINATED, PRODUCING A NEWFILL EDGE AND FACTOR OVER G AND S P(G, S)= i. P(i)P(G|i)P(S|i) Grade SAT New undirected fill edge Letter Job Happy
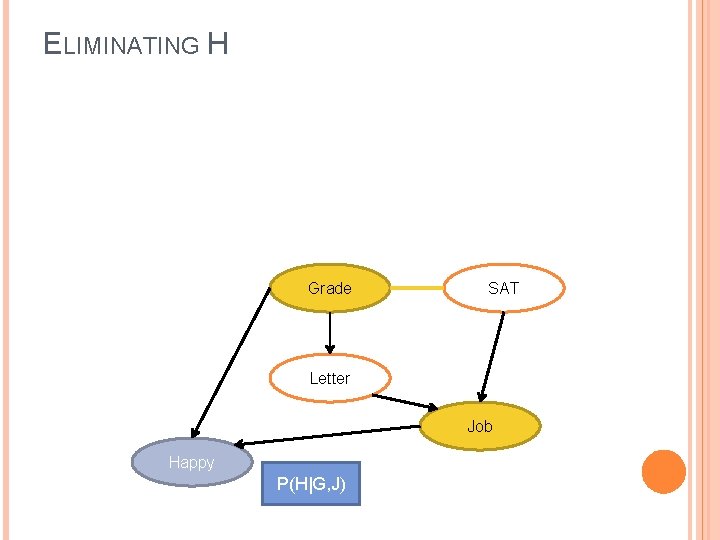
ELIMINATING H Grade SAT Letter Job Happy P(H|G, J)
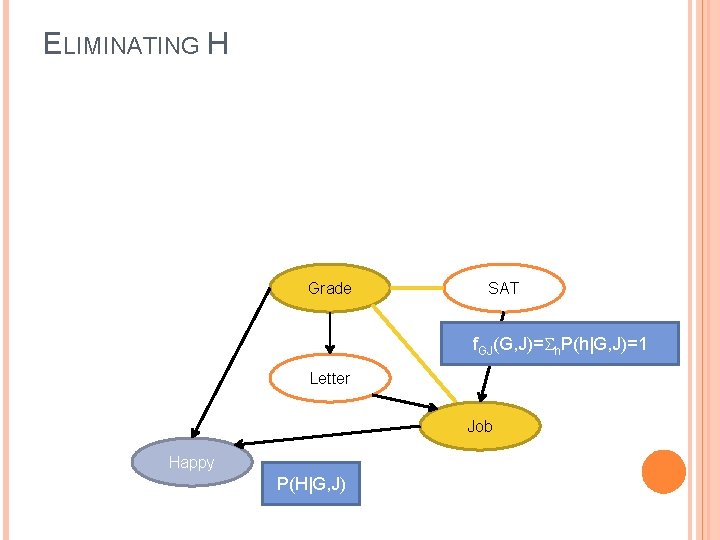
ELIMINATING H Grade SAT f. GJ(G, J)= h. P(h|G, J)=1 Letter Job Happy P(H|G, J)
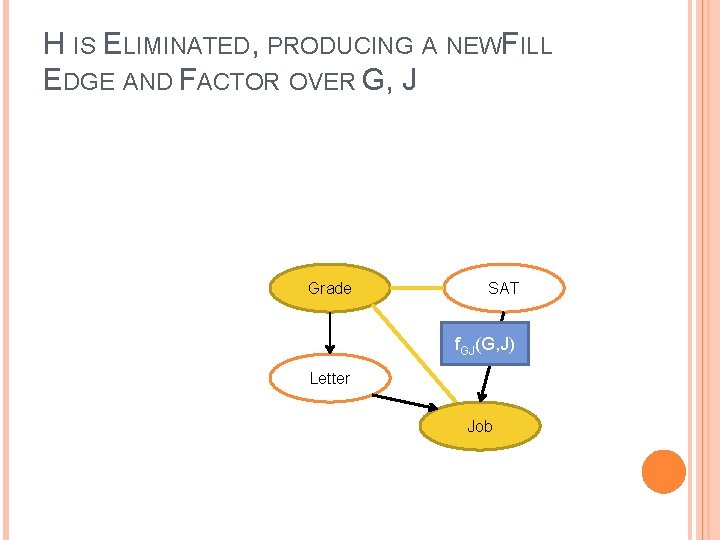
H IS ELIMINATED, PRODUCING A NEWFILL EDGE AND FACTOR OVER G, J Grade SAT f. GJ(G, J) Letter Job
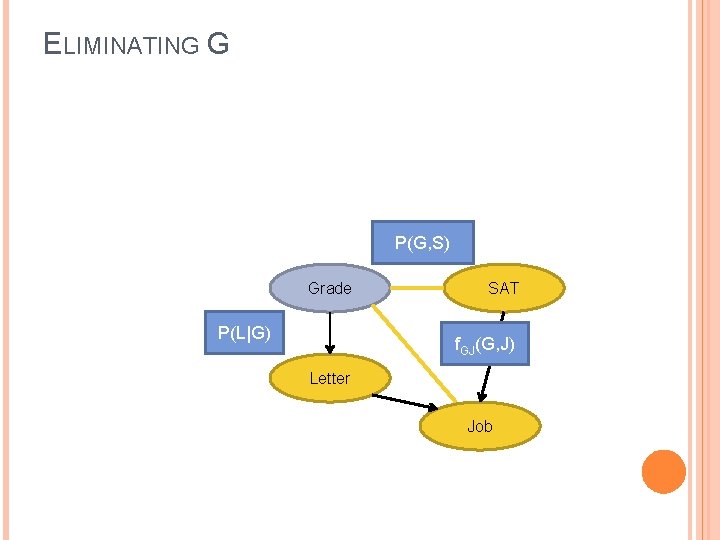
ELIMINATING G P(G, S) Grade P(L|G) SAT f. GJ(G, J) Letter Job
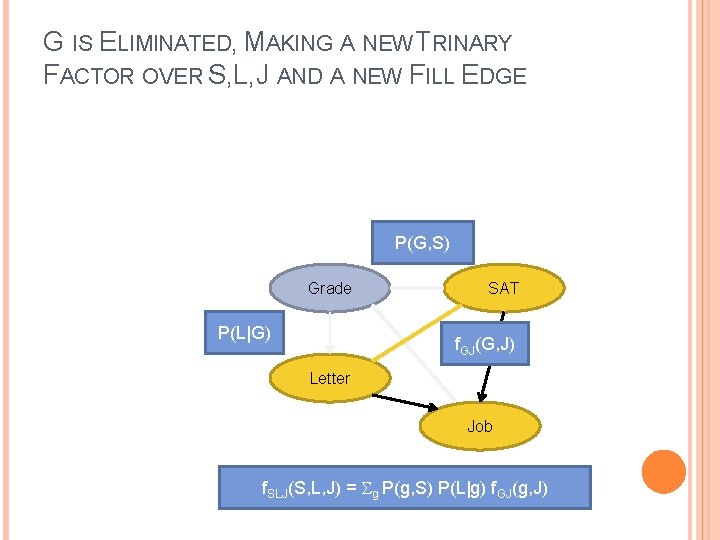
G IS ELIMINATED, MAKING A NEW TRINARY FACTOR OVER S, L, J AND A NEW FILL EDGE P(G, S) Grade P(L|G) SAT f. GJ(G, J) Letter Job f. SLJ(S, L, J) = g P(g, S) P(L|g) f. GJ(g, J)
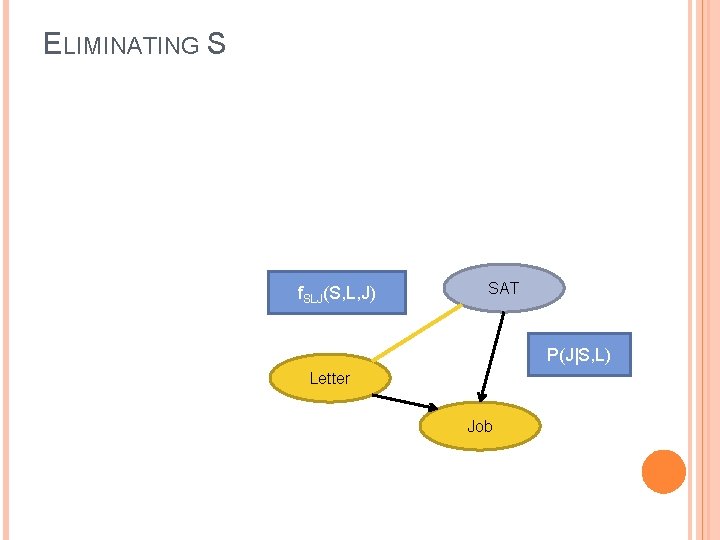
ELIMINATING S f. SLJ(S, L, J) SAT P(J|S, L) Letter Job
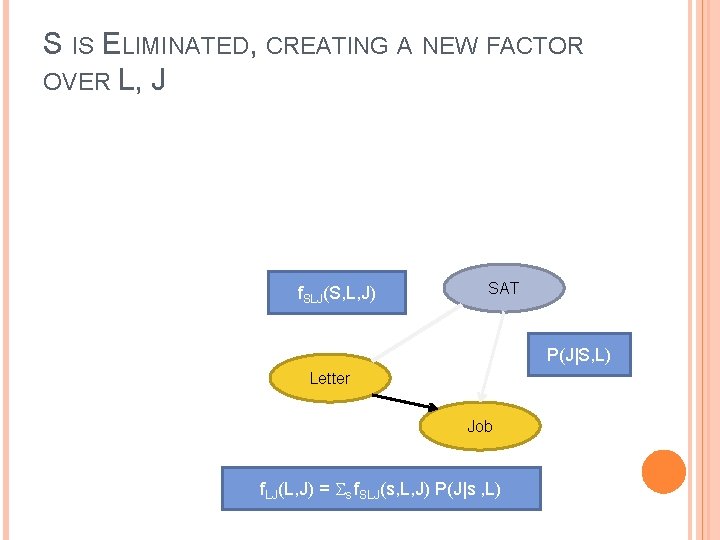
S IS ELIMINATED, CREATING A NEW FACTOR OVER L, J f. SLJ(S, L, J) SAT P(J|S, L) Letter Job f. LJ(L, J) = s f. SLJ(s, L, J) P(J|s , L)
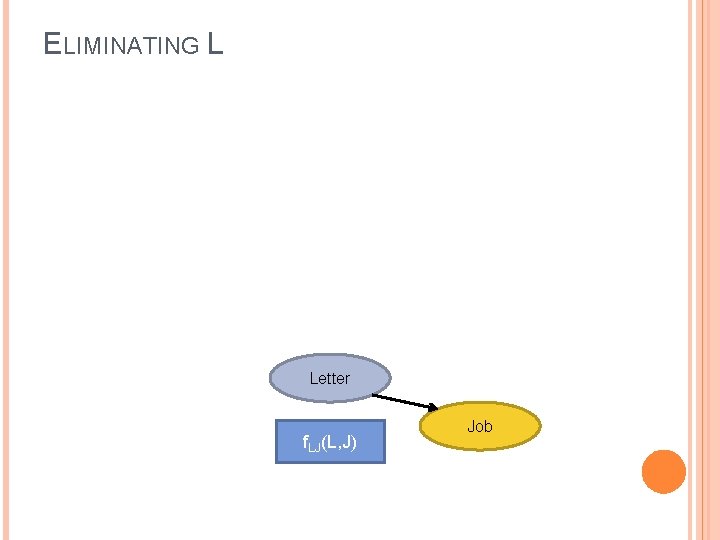
ELIMINATING L Letter f. LJ(L, J) Job
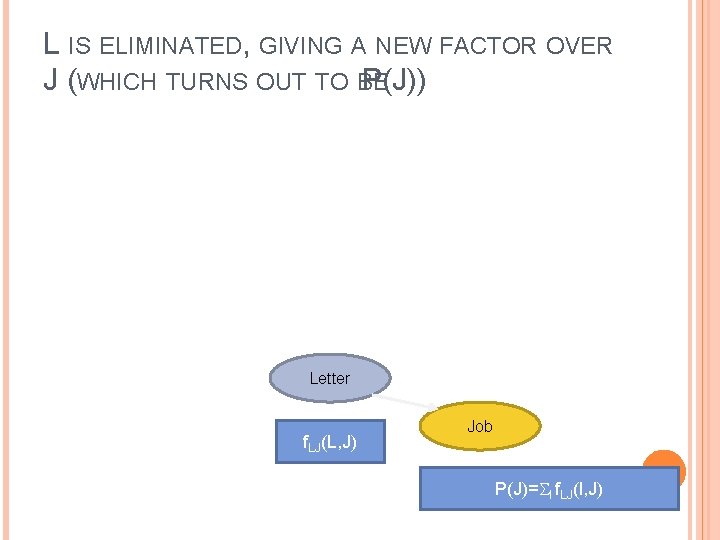
L IS ELIMINATED, GIVING A NEW FACTOR OVER J (WHICH TURNS OUT TO BE P(J)) Letter f. LJ(L, J) Job P(J)= l f. LJ(l, J)
L IS ELIMINATED, GIVING A NEW FACTOR OVER J (WHICH TURNS OUT TO BE P(J)) Job P(J)

JOINT DISTRIBUTION P(X) = P(C)P(D|C)P(I)P(G|I, D)P(S|I)P(L|G) P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L

GOING THROUGH VE P(X) = P(C)P(D|C)P(I)P(G|I, D)P(S|I)P(L|G) P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. D(D)= CP(C)P(D|C)

GOING THROUGH VE CP(X) = f. D(D)P(I)P(G|I, D)P(S|I)P(L|G) P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. D(D)= CP(C)P(D|C)

GOING THROUGH VE CP(X) = f. D(D)P(I)P(G|I, D)P(S|I)P(L|G) P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. GI(G, I)= Df. D(D)P(G|I, D)

GOING THROUGH VE C, DP(X) = f. GI(G, I)P(S|I)P(L|G) P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. GI(G, I)= Df. D(D)P(G|I, D)

GOING THROUGH VE C, DP(X) = f. GI(G, I)P(S|I)P(L|G) P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. GS(G, S)= If. GI(G, I)P(S|I)

GOING THROUGH VE C, D, IP(X) = f. GS(G, S)P(L|G)P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. GS(G, S)= If. GI(G, I)P(S|I)

GOING THROUGH VE C, D, IP(X) = f. GS(G, S)P(L|G)P(J|L, S)P(H|G, J) Apply elimination ordering C, D, I, H, G, S, L f. GJ(G, J)= HP(H|G, J) What values does this factor store?

GOING THROUGH VE C, D, I, HP(X) = f. GS(G, S)P(L|G)P(J|L, S)f. GJ(G, J) Apply elimination ordering C, D, I, H, G, S, L f. GJ(G, J)= HP(H|G, J)

GOING THROUGH VE C, D, I, HP(X) = f. GS(G, S)P(L|G)P(J|L, S)f. GJ(G, J) Apply elimination ordering C, D, I, H, G, S, L f. SLJ(S, L, J)= G f. GS(G, S)P(L|G)f. GJ(G, J)

GOING THROUGH VE C, D, I, H, GP(X) = f. SLJ(S, L, J)P(J|L, S) Apply elimination ordering C, D, I, H, G, S, L f. SLJ(S, L, J)= G f. GS(G, S)P(L|G)f. GJ(G, J)

GOING THROUGH VE C, D, I, H, GP(X) = f. SLJ(S, L, J)P(J|L, S) Apply elimination ordering C, D, I, H, G, S, L f. LJ(L, J)= S f. SLJ(S, L, J)P(J|L, S)

GOING THROUGH VE C, D, I, H, G, SP(X) = f. LJ(L, J) Apply elimination ordering C, D, I, H, G, S, L f. LJ(L, J)= S f. SLJ(S, L, J)

GOING THROUGH VE C, D, I, H, G, SP(X) = f. LJ(L, J) Apply elimination ordering C, D, I, H, G, S, L f. J(J)= L f. LJ(L, J)

GOING THROUGH VE C, D, I, H, G, S, LP(X) = f. J(J) Apply elimination ordering C, D, I, H, G, S, L f. J(J)= L f. LJ(L, J)

ORDER-DEPENDENCE
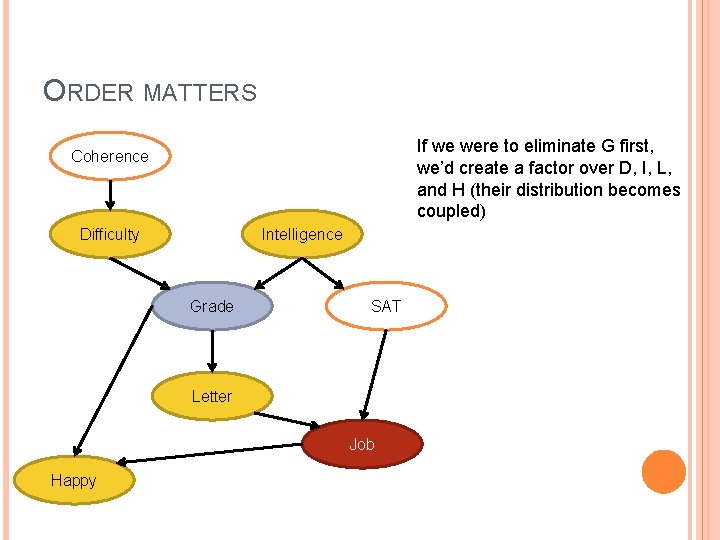
ORDER MATTERS If we were to eliminate G first, we’d create a factor over D, I, L, and H (their distribution becomes coupled) Coherence Difficulty Intelligence Grade SAT Letter Job Happy
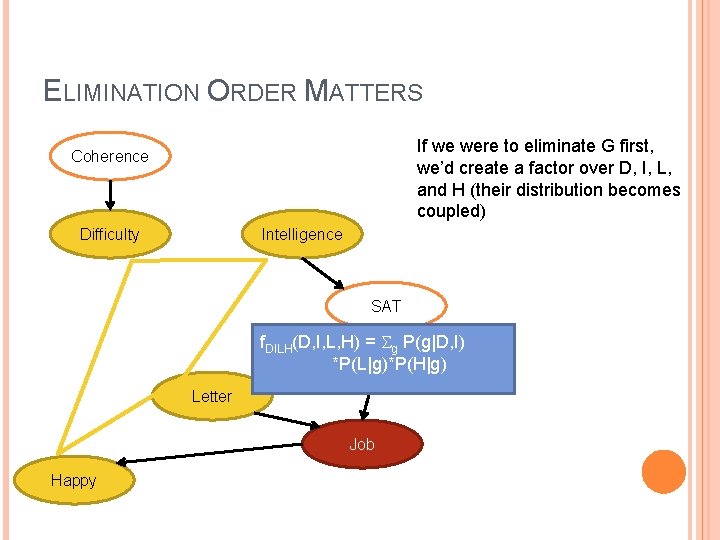
ELIMINATION ORDER MATTERS If we were to eliminate G first, we’d create a factor over D, I, L, and H (their distribution becomes coupled) Coherence Difficulty Intelligence SAT f. DILH(D, I, L, H) = g P(g|D, I) *P(L|g)*P(H|g) Letter Job Happy

COMPLEXITY In polytree networks where each node has at most k parents, O(n 2 k) with top-down ordering In other networks, intermediate factors may involve more than k terms � Worst case O(n) � Good ordering heuristics exist, e. g. min-neighbors, minfill Exact inference on non-polytree networks is NPhard!
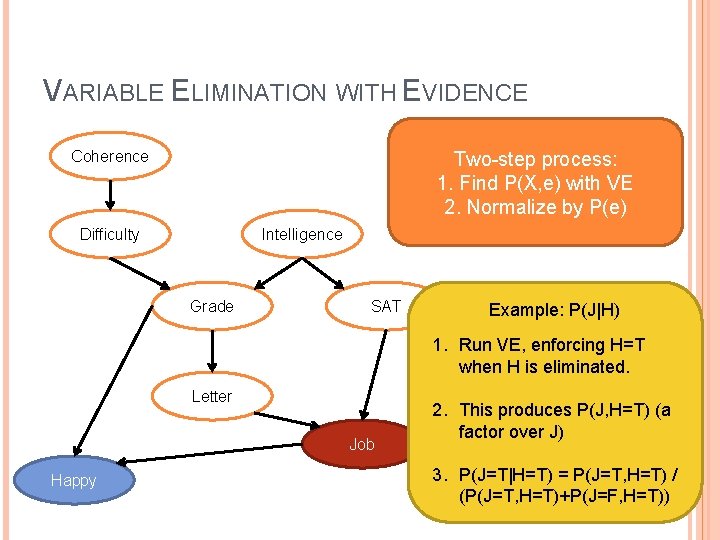
VARIABLE ELIMINATION WITH EVIDENCE Coherence Two-step process: 1. Find P(X, e) with VE 2. Normalize by P(e) Difficulty Intelligence Grade SAT Example: P(J|H) 1. Run VE, enforcing H=T when H is eliminated. Letter Job Happy 2. This produces P(J, H=T) (a factor over J) 3. P(J=T|H=T) = P(J=T, H=T) / (P(J=T, H=T)+P(J=F, H=T))

RECAP Exact inference techniques Top-down inference: linear time when ancestors of query variable are polytree, evidence is on ancestors Bottom-up inference in Naïve Bayes models General inference using Variable Elimination (We’ll come back to approximation techniques in a week. )

NEXT TIME Learning Bayes nets R&N 20. 1 -2
- Slides: 55