Bayesian Networks Probability In AI Bayes Theorem PAB

Bayesian Networks Probability In AI

Bayes’ Theorem • P(A|B) = P(B|A) P(A) / P(B)

Example • • • Bowl 1 – 10 red and 30 white balls Bowl 2 – 20 red and 20 white balls Randomly pick a bowl and then a ball from it What is P(Bowl 1 | white ball) ? By Bayes’ – P(white|bowl 1) P(bowl 1) / P(white) – P(white) =. 5 P(white|bowl 1) +. 5 P(white|bowl 2)

Bayesian Network • G=(V, E) be a DAG • Let each node be a random variable • For node a the nodes connected to a are {bi} – P(a|{bi}) (written in Conditional Probability Tables)
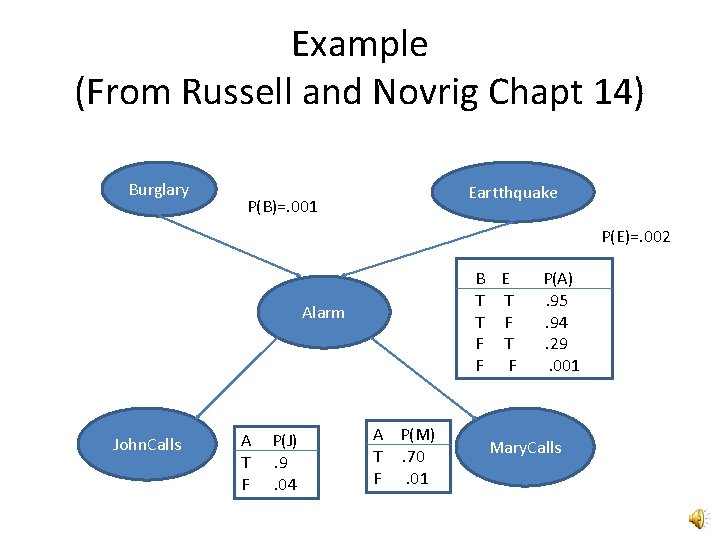
Example (From Russell and Novrig Chapt 14) Burglary Eartthquake P(B)=. 001 P(E)=. 002 B E T T T F F Alarm John. Calls A T F P(J). 9. 04 A P(M) T. 70 F. 01 P(A). 95. 94. 29. 001 Mary. Calls

Semantics • The graph represents the full joint probability distribution • P(x 1, …. xn) is the probability of the set of assignments to the variables • P(x 1, …. xn) = Pi=1, n P(xi | parents(Xi))

Construction • Nodes from the set of random variables – Order them with causes before effects(not required, but simpler!) • Links – For each node determine the set of parents – Link them – Define Conditional Probablity Table

Query • Given an observed event, what is posterior probability for the query variables. • Ex: P(Burglary | John. Calles = true , Mary. Calles = true) – Answer is <0. 284, 0. 716>

Method Single Variable by enumeration • Find P(X, e) – X is query variable – e is event : on the evidence variables – Y is a set of hidden variables • P(X|e) = a S P(X, e, y) – The constant a is to normalize

P(Burglary | John. Calles = true , Mary. Calles = true) • • P(B| j, m) =a P(B, j, m) = a Se Sa P(b, j, m, e, a) For CPT entries: For burglary = true: = a Se Sa P(b)P(e)P(a|b, e)P(j|a)P(m|a) This is. 00059224 For the false case -. 0014919 The a is computed to give a sum = 1

Variable Elimination • A query method that works by removing the unobserved variables • More efficient

Summary
- Slides: 12