Bayesian Networks in Bioinformatics KyuBaek Hwang Biointelligence Lab

Bayesian Networks in Bioinformatics Kyu-Baek Hwang Biointelligence Lab School of Computer Science and Engineering Seoul National University kbhwang@bi. snu. ac. kr Copyright (c) 2002 by SNU CSE Biointelligence Lab

Contents l Bayesian networks – preliminaries ¨ Bayesian networks vs. causal networks ¨ Partially DAG representation of the Bayesian network ¨ Structural learning of the Bayesian network ¨ Classification using Bayesian networks l Microarray data analysis with Bayesian networks ¨ Experimental results on the NCI 60 data set l Term Project #3 ¨ Diagnosis using Bayesian networks Copyright (c) 2002 by SNU CSE Biointelligence Lab 2

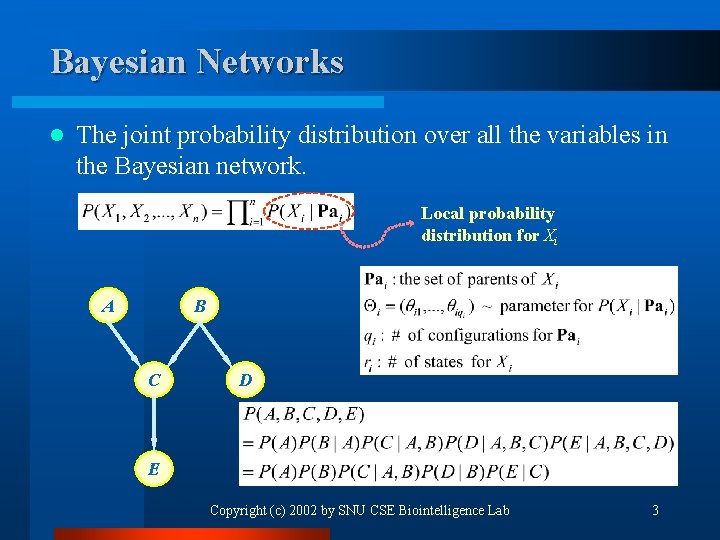
Bayesian Networks l The joint probability distribution over all the variables in the Bayesian network. Local probability distribution for Xi A B C D E Copyright (c) 2002 by SNU CSE Biointelligence Lab 3

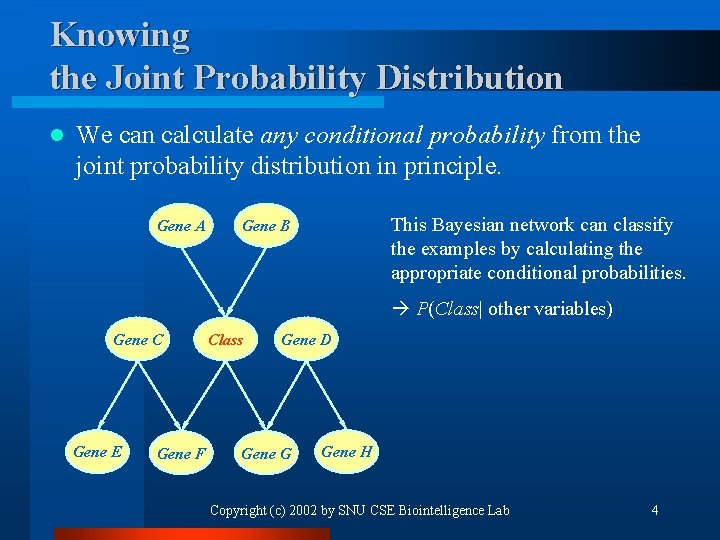
Knowing the Joint Probability Distribution l We can calculate any conditional probability from the joint probability distribution in principle. Gene A This Bayesian network can classify the examples by calculating the appropriate conditional probabilities. Gene B P(Class| other variables) Gene C Gene E Gene F Class Gene D Gene G Gene H Copyright (c) 2002 by SNU CSE Biointelligence Lab 4

Classification by Bayesian Networks I l Calculate the conditional probability of ‘Class’ variable given the value of the other variables. ¨ Infer the conditional probability from the joint probability distribution. ¨ For example, < where the summation is taken over all the possible class values. Copyright (c) 2002 by SNU CSE Biointelligence Lab 5

Knowing the Causal Structure Gene A Gene C regulates Gene E and F. Gene B Gene D regulates Gene G and H. Class has an effect on Gene F and G. Gene C Gene E Gene F Class Gene D Gene G Gene H Copyright (c) 2002 by SNU CSE Biointelligence Lab 6

Bayesian Networks vs. Causal Networks Network structure Bayesian networks Causal networks Conditional independencies Causal relationships By d-separation property of the Bayesian network structure The network structure asserts that every node is conditionally independent from all of its nondescendants given the values of its immediate parents. Copyright (c) 2002 by SNU CSE Biointelligence Lab 7

Equivalent Two DAGs X Y These two DAGs assert that X and Y are dependent on each other. the same conditional independencies X Y equivalence class Causal relationships are hard to learn from the observational data. Copyright (c) 2002 by SNU CSE Biointelligence Lab 8

Verma and Pearl’s Theorem l Theorem: ¨ Two DAGs are equivalent if and only if they have the same skeleton and the same v-structures. X Y v-structure (X, Z, Y) Z : X and Y are parents of Z and not adjacent to each other. Copyright (c) 2002 by SNU CSE Biointelligence Lab 9

PDAG Representations l Minimal PDAG representations of the equivalence class ¨ The only directed edges are those that participate in v-structures. l Completed PDAG representation ¨ Every directed edge corresponds to a compelled edge, and every undirected edge corresponds to a reversible edge. Copyright (c) 2002 by SNU CSE Biointelligence Lab 10

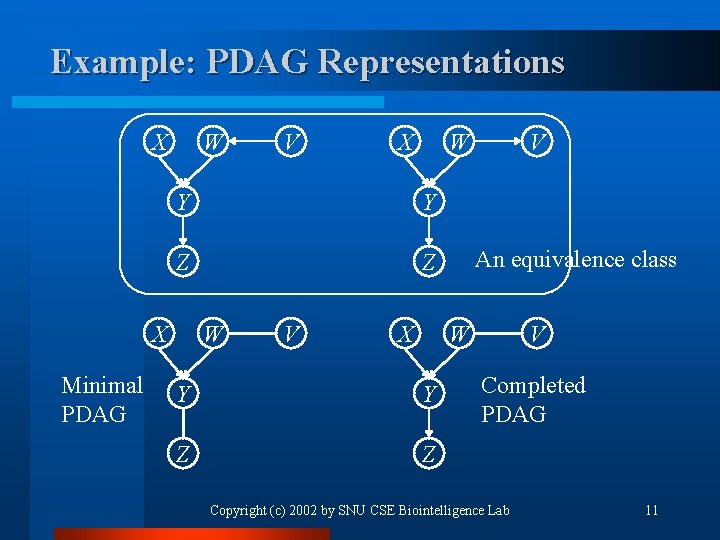
Example: PDAG Representations X W Y Y Z Z X Minimal PDAG V W

Learning Bayesian Networks l Metric approach ¨ Use a scoring metric to measure how well a particular structure fits an observed set of cases. ¨ A search algorithm is used. Find a canonical form of an equivalence class. l Independence approach ¨ An independence oracle (approximated by some statistical test) is queried to identify the equivalence class that captures the independencies in the distribution from which the data was generated. Search for a PDAG Copyright (c) 2002 by SNU CSE Biointelligence Lab 12

Scoring Metrics for Bayesian Networks l Likelihood L(G, G, C) = P(C|Gh, G) ¨ Gh: the hypothesis that the data (C) was generated by a distribution that can be factored according to G. l The maximum likelihood metric of G prefer the complete graph structure Copyright (c) 2002 by SNU CSE Biointelligence Lab 13

Information Criterion Scoring Metrics l The Akaike information criterion (AIC) metric l The Bayesian

MDL Scoring Metrics l The minimum description length (MDL) metric 1 Copyright (c) 2002

Bayesian Scoring Metrics l A Bayesian metric l The BDe (Bayesian Dirichlet & likelihood

Greedy Search Algorithm for Bayesian Network Learning Generate the initial Bayesian network structure G 0. l For m = 1, 2, 3, …, until convergence. l ¨ Among all the possible local changes (insertion of an edge, reversal of an edge, and deletion of an edge) in Gm– 1, the one leads to the largest improvement in the score is performed. The resulting graph is Gm. l Stopping criterion ¨ Score(Gm– 1) == Score(Gm). l At each iteration (learning Bayesian network consisting of n variables) ¨ O(n 2) local changes should be evaluated to select the best one. l Random restarts is usually adopted to escape the local maxima. Copyright (c) 2002 by SNU CSE Biointelligence Lab 17

Probabilistic Inference l Calculate the conditional probability given the values of the observed variables. ¨ Junction tree algorithm ¨ Sampling method ¨ General probabilistic inference is intractable. < However, calculation of the conditional probability for the classification is rather straightforward because of the property of the Bayesian network structure. Copyright (c) 2002 by SNU CSE Biointelligence Lab 18

The Markov Blanket l All the variables of interest ¨ X = {X 1, X 2, …, Xn} l For a variable Xi, its Markov blanket MB(Xi) is the subset of X – Xi which satisfies the following: l Markov boundary ¨ Minimal Markov blanket Copyright (c) 2002 by SNU CSE Biointelligence Lab 19

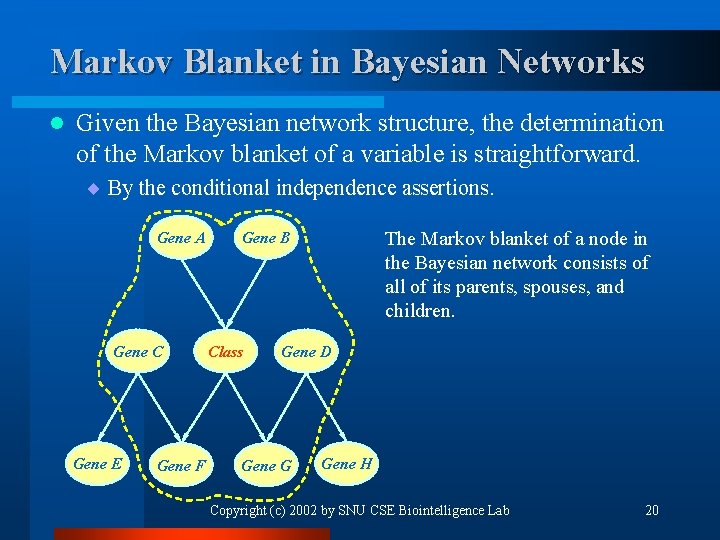
Markov Blanket in Bayesian Networks l Given the Bayesian network structure, the determination of the Markov blanket of a variable is straightforward. ¨ By the conditional independence assertions. Gene A Gene C Gene E Gene F The Markov blanket of a node in the Bayesian network consists of all of its parents, spouses, and children. Gene B Class Gene D Gene G Gene H Copyright (c) 2002 by SNU CSE Biointelligence Lab 20

Classification by Bayesian Networks II Copyright (c) 2002 by SNU CSE Biointelligence Lab 21

DNA Microarrays Monitor thousands of gene expression levels simultaneously traditional one gene experiments. l Fabricated by high-speed robotics. l Known probes Copyright (c) 2002 by SNU CSE Biointelligence Lab 22

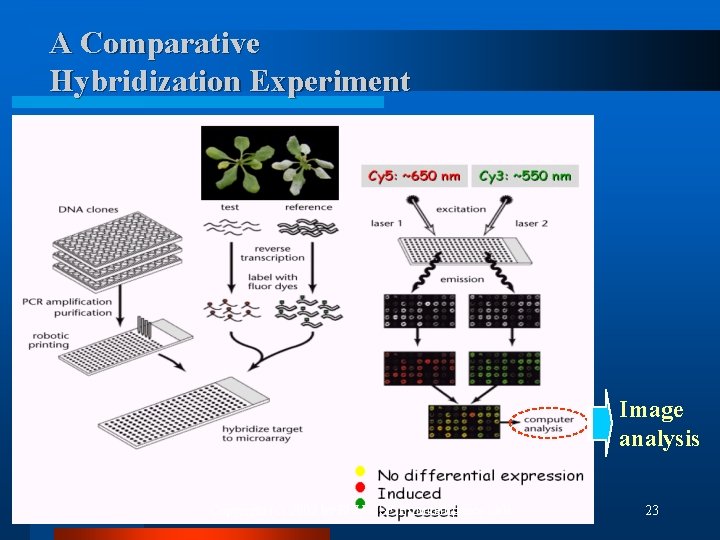
A Comparative Hybridization Experiment Image analysis Copyright (c) 2002 by SNU CSE Biointelligence Lab

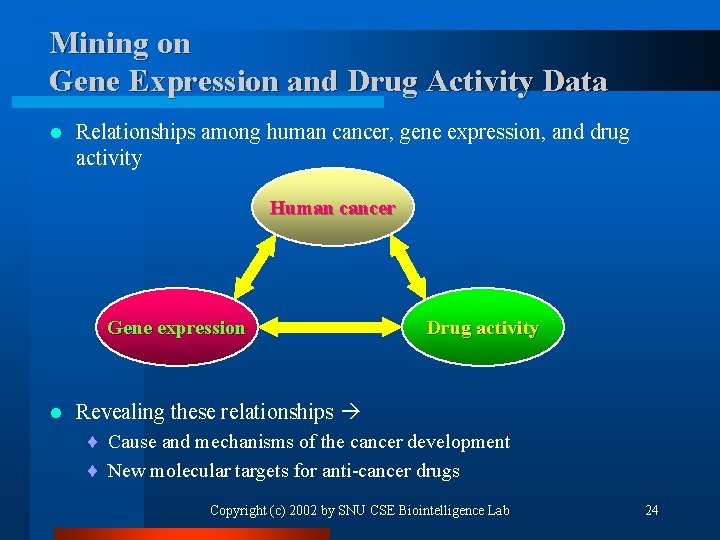
Mining on Gene Expression and Drug Activity Data l Relationships among human cancer, gene expression, and drug activity Human cancer Gene expression l Drug activity Revealing these relationships ¨ Cause and mechanisms of the cancer development ¨ New molecular targets for anti-cancer drugs Copyright (c) 2002 by SNU CSE Biointelligence Lab 24

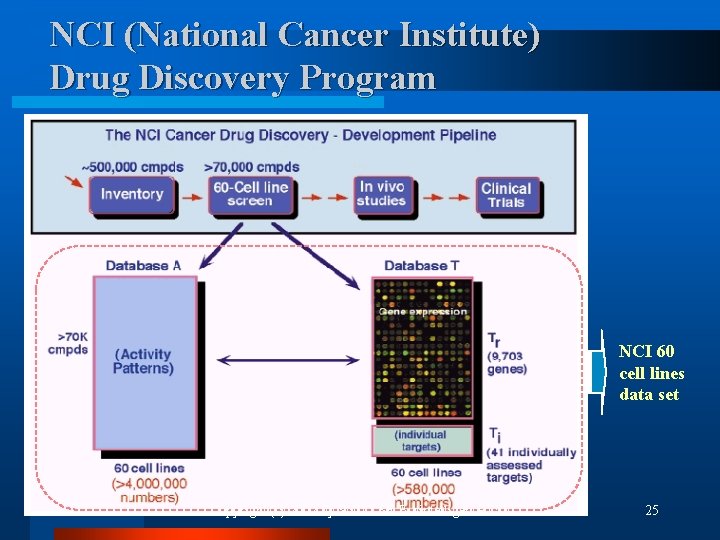
NCI (National Cancer Institute) Drug Discovery Program NCI 60 cell lines data set Copyright

NCI 60 Cell Lines Data Set l From 60 human cancer cell lines ¨ Colorectal, renal, ovarian, breast, prostate, lung, and central nervous system origin cancers, as well as leukemias and melanomas l Gene expression patterns ¨ c. DNA microarray l Drug activity patterns ¨ Sulphorhodamine B assay changes in total cellular protein after 48 hours of drug treatment Copyright (c) 2002 by SNU CSE Biointelligence Lab 26

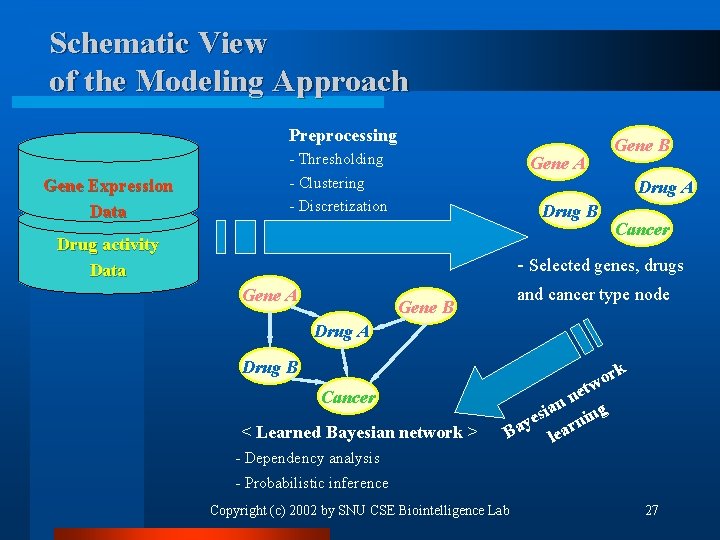
Schematic View of the Modeling Approach Preprocessing Gene Expression Data - Thresholding - Clustering - Discretization Gene A Gene B Drug A Drug B Drug activity Data Cancer - Selected genes, drugs Gene A and cancer type node Gene B Drug A Drug B Cancer < Learned Bayesian network > rk o etw n an ng i s ye arni a B le - Dependency analysis - Probabilistic inference Copyright (c) 2002 by SNU CSE Biointelligence Lab 27

Data Preparation l c. DNA microarray data l Drug activity data (1376 + 118) 60 data matrix 1376 genes 60 samples Drug activities ¨ Drug activity patterns on 60 cell lines ¨ 118 60 matrix Gene expressions ¨ Gene expression profiles on 60 cell lines ¨ 1376 60 matrix 60 samples Copyright (c) 2002 by SNU CSE Biointelligence Lab 118 drugs 28

Preprocessing l ¨ Elimination of unknown ESTs 805 genes ¨ Elimination of drugs which have more than 4 missing values 84 drugs l 60 samples Thresholding 60 samples 1376 genes 805 genes 84 drugs 118 drugs Discretization ¨ Local probability model for Bayesian networks: multinomial distribution 0 -1 1 - c Copyright (c) 2002 by SNU CSE Biointelligence Lab + c 29

Bayesian Network Learning for Gene-Drug Analysis l Large-scale Bayesian network ¨ Several hundreds nodes (up to 890) ¨ General greedy search is inapplicable because of time and space complexity. l Search heuristics ¨ Local to global search heuristics ¨ Exploit the locality of Bayesian networks to reduce the entire search space. < The local structure: Markov blanket < Find the candidate Markov blanket (of pre-determined size k) of each node reduce the global search space Copyright (c) 2002 by SNU CSE Biointelligence Lab 30

Local to Global Search Heuristics Input: - A data set D. - An initial Bayesian network structure B 0. - A decomposable scoring metric, Output: A Bayesian network structure B. Loop for n = 1, 2, …, until convergence. - Local Search Step: * Based on D and Bn– 1, select for Xi, a set CBin (|CBin| k) of candidate Markov blanket of Xi. * For each set {Xi, CBin}, learn the local structure and determine the Markov blanket of Xi, BLn(Xi), from this local structure. * Merge all Markov blanket structures G({Xi, BLn(Xi)}, Ei) into a global network structure Hn (could be cyclic). - Global Search Step: * Find the Bayesian network structure Bn Hn, which maximizes Score(Bn, D) and retains all noncyclic edges in Hn. Copyright (c) 2002 by SNU CSE Biointelligence Lab 31

Dimensionality Problem l The number of attributes (nodes) >> sample size ¨ Unreliable structure of the learned Bayesian networks ¨ Probabilistic inference is nearly impossible. l Downsize the number of attributes by clustering ¨ Prototype: mean of all members in a cluster In the preprocessing step Copyright (c) 2002 by SNU CSE Biointelligence Lab 32

Bayesian Network with 45 Prototypes l Node types (46 nodes in all) ¨ 40 gene prototypes ¨ 5 drug prototypes ¨ Cancer label l Discretization boundary ¨ - c , + c c Distribution Ratio -1 0 1 0. 43 33. 3% 0. 50 30. 8% 38. 3% 30. 8% 0. 60 27. 4% 45. 1% 27. 4% l Bayesian network learning ¨ Varying candidate Markov blanket size (k = 5 ~ 15) ¨ Select the best one ¨ Three data sets (c = 0. 43, 0. 50, 0. 60) three Bayesian networks ¨ Probabilistic inference Copyright (c) 2002 by SNU CSE Biointelligence Lab 33

Correlations between ASNS and L-Asparaginase l Part of the Bayesian network (c = 0. 60) < Conditional probability table > Prototype for L-Asparaginase P(D 2|G 4 ) D 2 = -1 D 2 = 0 D 2 = 1 G 4 = -1 0. 32096 0. 27086 0. 40818 G 4 = 0 0. 31387 0. 41247 0. 27366 G 4 = 1 0. 32167 0. 34920 0. 32913 Prototype for ASNS and SID W 484773, PYRROLINE-5 CARBOXYLATE REDUCTASE [5': AA 037688, 3': AA 037689] Copyright (c) 2002 by SNU CSE Biointelligence Lab 34

Bayesian Networks on Subset of Genes and Drugs l Node types (17 nodes in all) ¨ 12 genes ¨ 4 drugs ¨ Cancer label l Discretization boundary ¨ - c , + c c Distribution Ratio -1 0 1 0. 43 33. 3% 0. 50 30. 8% 38. 3% 30. 8% 0. 60 27. 4% 45. 1% 27. 4% l Clustering of genes and drugs together - From neighboring clusters Bayesian network learning ¨ General greedy search with restart (100 times) ¨ Select the best one ¨ Three data sets (c = 0. 43, 0. 50, 0. 60) three Bayesian networks ¨ Probabilistic inference Copyright (c) 2002 by SNU CSE Biointelligence Lab 35

Around the L-Asparaginase < Part of the Bayesian network (c = 0. 6) >

Probabilistic Relationships Around the L-Asparaginase l Cancer type unobserved l ¨ D 1: L-Asparaginase ¨ G 1: ASNS gene ¨ G 2: PYRROLINE-5 -CARBOXYLATE REDUCTASE P(D 1|G 1) D 1 = -1 D 1 = 0 D 1 = 1 G 1 = -1 0. 19857 0. 27471 0. 52672 G 1 = 0 0. 31110 0. 49795 0. 19095 G 1 = 1 0. 42159 0. 36279 0. 21561 P(D 1|G 2) D 1 = -1 D 1 = 0 D 1 = 1 G 2 = -1 0. 27510 0. 35226 0. 37263 G 2 = 0 0. 31621 0. 41072 0. 27307 G 2 = 1 0. 33837 0. 39664 0. 26499 Cancer type observed (= leukemia) ¨ D 1: L-Asparaginase ¨ G 1: ASNS gene ¨ G 2: PYRROLINE-5 -CARBOXYLATE REDUCTASE P(D 1|G 1, L ) D 1 = -1 D 1 = 0 D 1 = 1 G 1 = -1 0. 17536 0. 22838 0. 59626 G 1 = 0 0. 27128 0. 53790 0. 19081 G 1 = 1 0. 38500 0. 42437 0. 19063 P(D 1|G 2, L ) D 1 = -1 D 1 = 0 D 1 = 1 G 2 = -1 0. 23812 0. 33853 0. 42335 G 2 = 0 0. 27978 0. 42666 0. 29356 G 2 = 1 0. 30371 0. 42108 0. 27520 Copyright (c) 2002 by SNU CSE Biointelligence Lab 37

Term Project #3: Diagnosis Using Bayesian Networks Copyright (c) 2002 by SNU CSE Biointelligence

Outline l Task 1: Structural learning of the Bayesian network ¨ Data generation from the ALARM network ¨ Structural learning of Bayesian networks using more than two kinds of algorithms and scores ¨ Compare the learned results w. r. t. the edge errors according to the various sample sizes and the learning algorithms l Task 2: Classification using Bayesian networks ¨ Arbitrarily divide the Leukemia data set between the training set and the test set ¨ Learn the Bayesian network from the training data set using one of the metric-based approaches ¨ Evaluate the performance of the Bayesian network as a classifier (classification accuracy) Copyright (c) 2002 by SNU CSE Biointelligence Lab 39

Data Generation Using the Netica Software (http: //www. norsys. com) l The ALARM network

Structural Learning l Independence method ¨ BN Power constructor (http: //www. cs. ualberta. ca/~jcheng/bnsoft. htm) l Metric-based method ¨ Learn. Bayes (http: //www. cs. huji. ac. il/labs/compbio/Lib. B/) ¨ MDL, BIC, BD, and likelihood score are can be used. Copyright (c) 2002 by SNU CSE Biointelligence Lab 41

The Leukemia Data Set l Class type ¨ ALL (acute lymphoblastic leukemia) or AML (acute myeloid leukemia) l Data set ¨ # of attributes: 50 gene expression levels (0 or 1) ¨ # of samples: 72 Copyright (c) 2002 by SNU CSE Biointelligence Lab 42