Bayesian Model Selection Bayesian Model Selection Bayesian Probability

Bayesian Model Selection

Bayesian Model Selection

Bayesian Probability Reason about hypotheses by assigning probabilities to them. – Often compared to frequentist approach, which tests a hypothesis without assigning a probability. Probability represents state of knowledge.
![Bayesian Probability Bayes’[1] theorem: Use this (along with prior beliefs) to update probability of Bayesian Probability Bayes’[1] theorem: Use this (along with prior beliefs) to update probability of](http://slidetodoc.com/presentation_image_h2/2b1cb9caeadf9f521dd89bb38390aaf7/image-4.jpg)
Bayesian Probability Bayes’[1] theorem: Use this (along with prior beliefs) to update probability of a model (M) based on new data (D). [1] Obviously not actually due to Bayes, see Stigler’s law of eponymy.

Model Selection “All models are wrong but some are useful. ” – Oscar Wilde George Box Occam’s Razor: Aim to find the simplest model which explains the observations. Frequentist approaches: hypothesis test, likelihood ratio test – nested models

Inter-related goals of model selection Parsimonious model (Occam’s Razor) Improved generalisation error Reduce overfitting

Bayesian Model Selection Compare models by comparing their posterior probabilities (marginalising over all possible parameters) Bayes factor

Benefits Naturally incorporates relative complexity of models to prevent overfitting Works for non-nested models Provides strength of evidence for each model

When to use it Genuinely discrete models Non-arbitrary choice of prior
![When to use it - example [1] Kass, R. E. and Raftery, A. E. When to use it - example [1] Kass, R. E. and Raftery, A. E.](http://slidetodoc.com/presentation_image_h2/2b1cb9caeadf9f521dd89bb38390aaf7/image-11.jpg)
When to use it - example [1] Kass, R. E. and Raftery, A. E. , 1995. Bayes factors. Journal of the american statistical association, 90(430), pp. 773 -795.

Escherichia coli mutagenesis
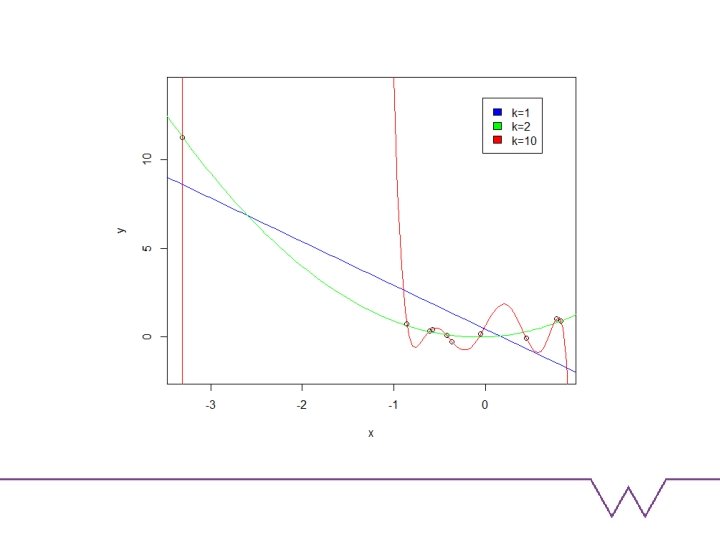
When not to use it Selecting between models derived from an underlying continuous model Arbitrary choice of prior Possible Bayesian approach to problems of this sort is to use a hierarchical model over a continuous family of models

How to use it Monte Carlo simulation of the posteriors – Computationally expensive Approximation using Bayesian Information Criterion (BIC) – Less expensive, but requires assumptions about the distribution of data – Sample size must be much larger than the number of parameters to estimate.

In Conclusion Model selection using Bayes’ factors: – Selects between discrete models – Controls for overfitting – Is possible to do cheaply using approximations But: – Approximation assumes large sample size – Other methods are more appropriate for continuous models.
- Slides: 15