Bayesian Model of Cognition Example Document Clustering Each

Bayesian Model of Cognition

Example: Document Clustering • Each document is a ‘bag of (content) words’ • How many clusters? In parametric methods the number of clusters is specified at the outset. Bayesian nonparametric methods (Gaussian Processes and Dirichlet Processes) automatically detect how many clusters there are.

Document Parameters • Any text document consists of words ( after removing the stop words). • A code book consists of whole words can be appeared in any text. – v is number of words in the code book. • Any word in the code book is a feature. The number of times a word appears in a text is its feature value. – v is the number of features in the problem. • A data set consists of n documents. Document i is presented by its feature vector xi and class label zi.

A Matrix Representation n Data Points: Class Labels (Hidden): c is number of classes (clusters)

Feature Probability • Feature j appears in a text document with φj probability. • Document i consisting of n 1 of word 1, n 2 of word 2, …, nv of wordv. So, xi=[ n 1, n 2, …, nv]T. – The words supposed to be mutually exclusive. – P(xi) has a multinomial distribution.

Multinomial Distribution • A multinomial probability distribution is a distribution over all the possible outcomes of multinomial experiment. A fair dice 1 2 3 4 5 6 A weighted dice If x is five draws for experiment: x = 5, 2, 3, 2, 6

Random Feature Values • • Values of φ may have uncertainty. So, φj is supposed to be random a variable. Dirichlet distribution is one choice for φ. Vector α=[α 1, α 2, ···, αv]T is the parameter of Dirichlet distribution.

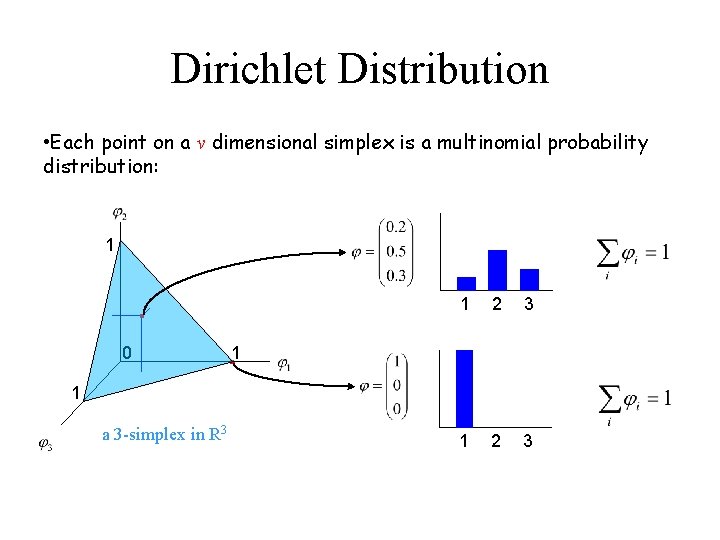
Dirichlet Distribution • Each point on a v dimensional simplex is a multinomial probability distribution: 1 0 1 2 3 1 1 a 3 -simplex in R 3

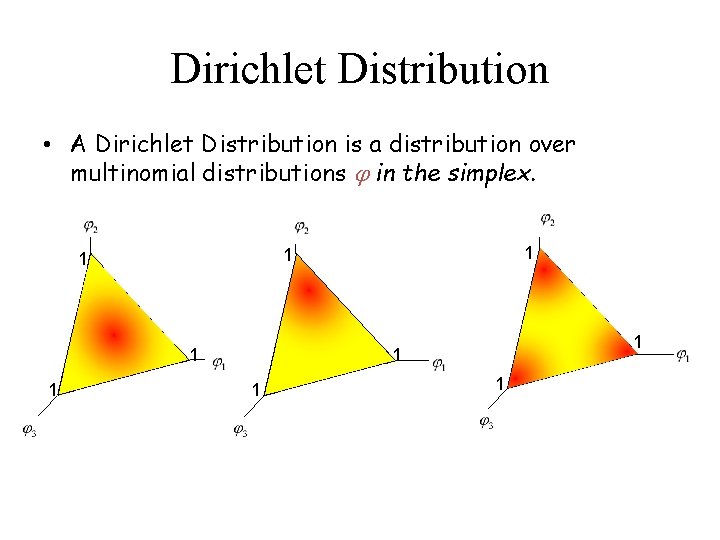
Dirichlet Distribution • A Dirichlet Distribution is a distribution over multinomial distributions in the simplex. 0 1 1 1 0 1 1

Dirichlet Distribution • The Dirichlet Distribution is parameterised by a set of concentration constants defined over the v-simplex A draw from a Dirichlet Distribution written as: where is a multinomial distribution over v outcomes.

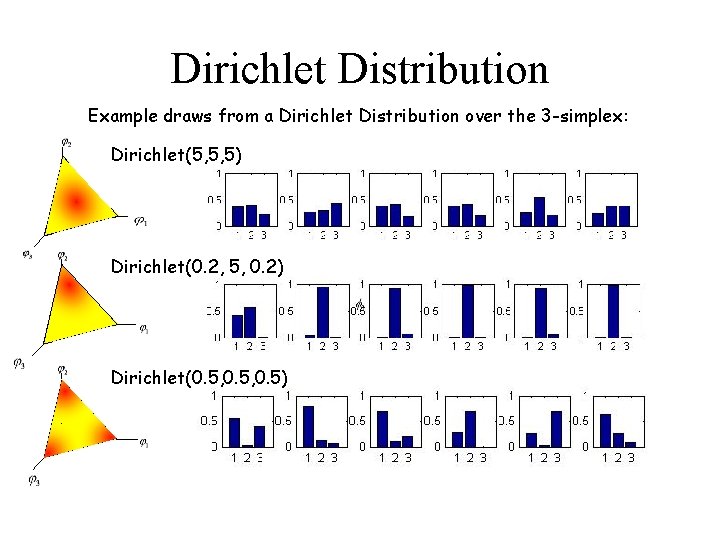
Dirichlet Distribution Example draws from a Dirichlet Distribution over the 3 -simplex: Dirichlet(5, 5, 5) 0 1 Dirichlet(0. 2, 5, 0. 2) 0 Dirichlet(0. 5, 0. 5)

Class Labels ( No. of Clusters) • z (the class label vector of data set) is hidden. • For a two class case, z’s elements are either 1 or 2. n 1 is number of 1 s and n 2 is number of 2 s. n 1+n 2=n • z can be generated by a multinomial distribution. • β itself may has uncertainty, therefore comes from a Dirichlet distribution.

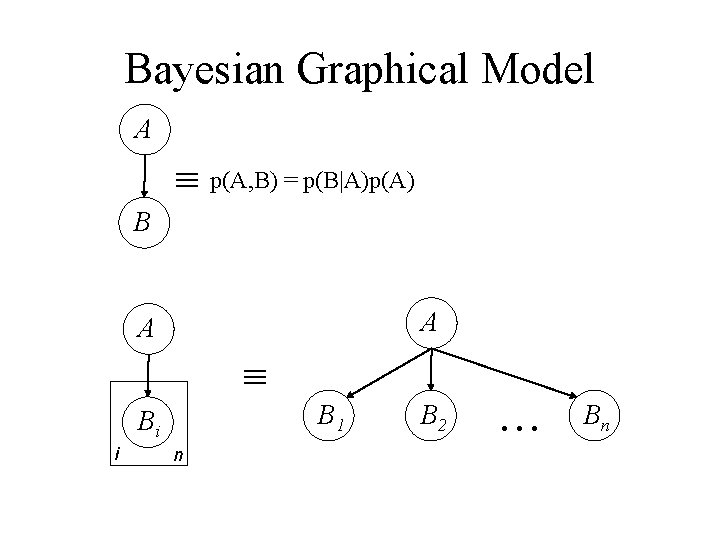
Bayesian Graphical Model A p(A, B) = p(B|A)p(A) B A A B 1 Bi i n B 2 Bn

Bayesian Finite Mixture Model Parameters: = ( , ) = ( 1 … c, 1 … v ) Hidden variables z = (z 1 … zn) Observed data x = (x 1 … xn) z zi z xi i n v

Bayesian Finite Mixture Model ~ Dirichletc( , …, ) Components z (z (1 … n)) are drawn from a base measure G 0 z ~ G 0 (e. g. Dirichletv( , …, )) For each data point (document) a component z is drawn: zi ~ Multinomial( ) and the data point is drawn from some distribution F( ). xi ~ F( zi ) (e. g. Multinomial( zi ))

Bayesian Finite Mixture Model Document clustering example: c = 2 clusters ~Dirichletk( , ) v = 3 word types z 1 z ~ Dirichletv( , , ) 1 2 3 z 2 1 2 3 i {1, … n}: z 1 = 1 z 2 = 2 z 3 = 2 z 4 = 1 z 5 = 2 Choose a source for each data point (document) zi ~ Multinomialc( ) Generate the data point (words in document) using source: xi ~ Multinomialv( z )) x 1 = ACAAB x 2 = ACCBCC x 3 = CCC x 4 = CABAAC x 5 = ACC

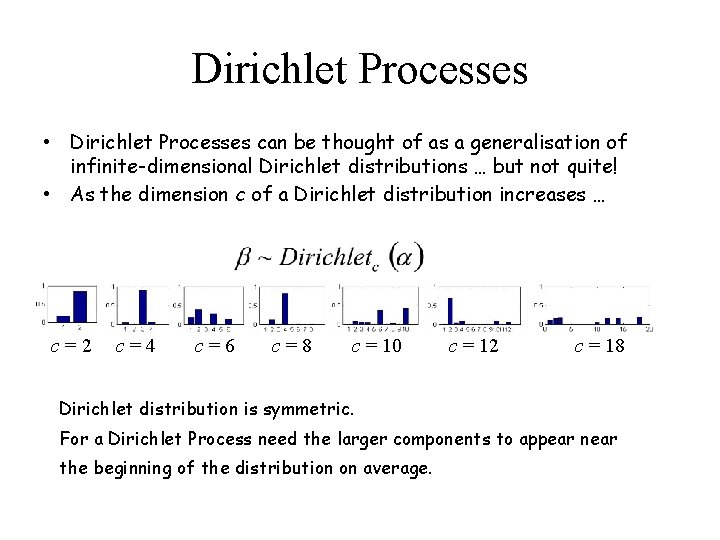
Dirichlet Processes • Dirichlet Processes can be thought of as a generalisation of infinite-dimensional Dirichlet distributions … but not quite! • As the dimension c of a Dirichlet distribution increases … c=2 c=4 c=6 c=8 c = 10 c = 12 c = 18 Dirichlet distribution is symmetric. For a Dirichlet Process need the larger components to appear near the beginning of the distribution on average.

Dirichlet Processes Mixture Model • Definition ~ Dirichletk( , …, ) GEM( ) Components z z (1 … k) (1 … ) z ~ G 0 For each data point (document) z is drawn: zi ~ Multinomial( ) and the data point is drawn from some distribution F( ) xi ~ F( z ) (e. g. Multinomial( z )) i i GEM: Generalized Exponential Models

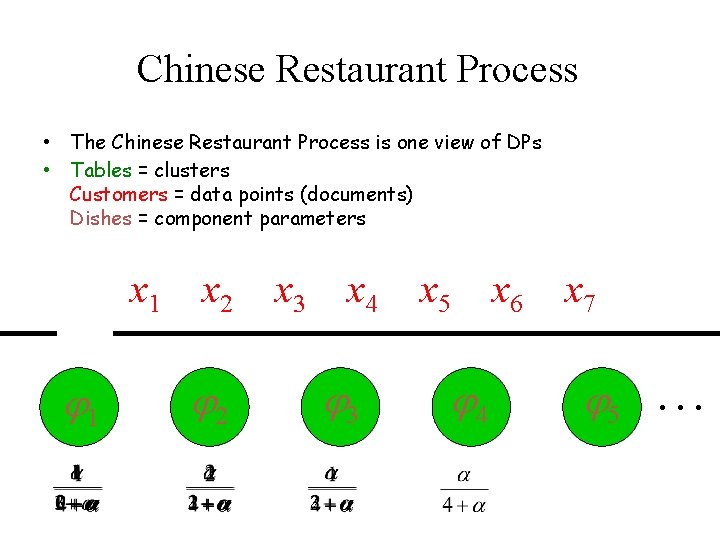
Chinese Restaurant Process • The Chinese Restaurant Process is one view of DPs • Tables = clusters Customers = data points (documents) Dishes = component parameters x 1 1 x 2 2 x 3 x 4 3 x 5 4 x 6 x 7 5 …

Chinese Restaurant Process • Shut your eyes if you don’t want to see any more maths … i | 1, …, i-1 ~ The “rich get richer” principle: tables with more customers get more customers on average

CRP Initial Clustering Demo • Initial table allocations • 100 documents 3 sources 5 to 20 words per document

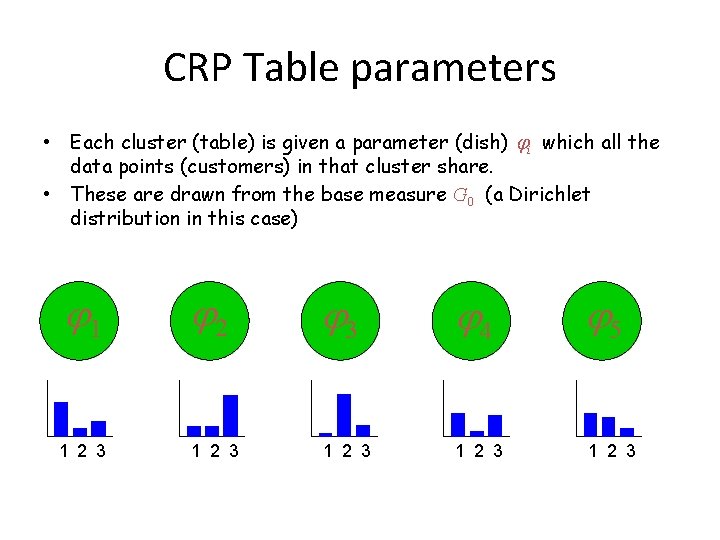
CRP Table parameters • Each cluster (table) is given a parameter (dish) i which all the data points (customers) in that cluster share. • These are drawn from the base measure G 0 (a Dirichlet distribution in this case) 1 1 2 3 2 3 4 5 1 2 3

CRP Inference • Goal of Bayesian inference is to calculate the posterior: p( , , z | x) The posterior cannot usually be sampled directly. Can use Gibbs sampling … z zi z xi i n k

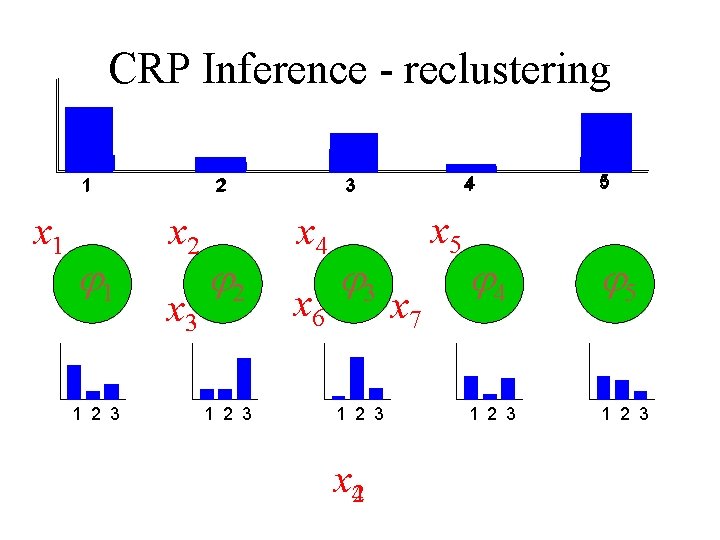
CRP Inference - reclustering 1 x 1 1 1 2 3 2 x 3 2 1 2 3 3 x 4 x 6 3 1 2 3 x 42 x 5 x 7 4 5 4 5 1 2 3

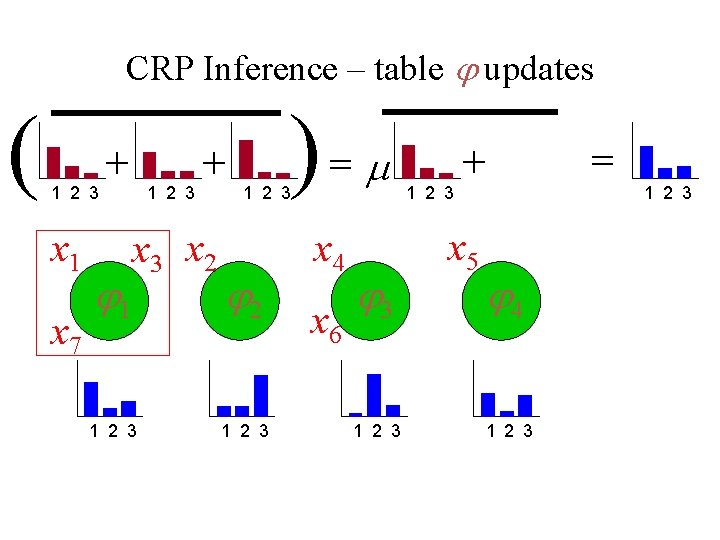
CRP Inference – table updates ( 1 2 3 x 1 x 7 + 1 1 2 3 + x 3 x 2 1 2 3 )= 1 2 3 2 1 2 3 x 4 x 6 3 1 2 3 = + x 5 1 2 3 4 1 2 3