Bayesian Learning Rong Jin Outline MAP learning vs

Bayesian Learning Rong Jin

Outline • • MAP learning vs. ML learning Minimum description length principle Bayes optimal classifier Bagging

Maximum Likelihood Learning (ML) • Find the best model by maximizing the loglikelihood of the training data
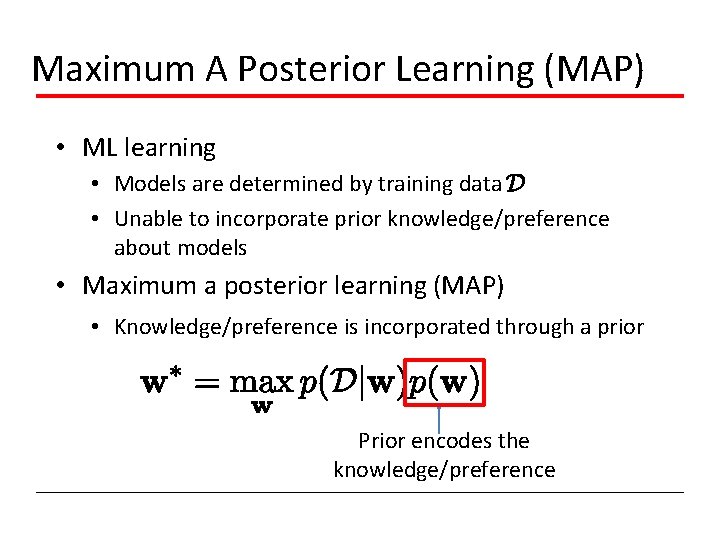
Maximum A Posterior Learning (MAP) • ML learning • Models are determined by training data • Unable to incorporate prior knowledge/preference about models • Maximum a posterior learning (MAP) • Knowledge/preference is incorporated through a prior Prior encodes the knowledge/preference

MAP • Uninformative prior: regularized logistic regression

MAP Consider text categorization • wi: importance of i-th word in classification • Prior knowledge: the more common the word, the less important it is • How to construct a prior according to the prior knowledge ?

MAP • An informative prior for text categorization • i : the occurrence of the i-th word in training data

MAP Two correlated classification tasks: C 1 and C 2 • How to introduce an appropriate prior to capture this prior knowledge ?

MAP • Construct priors to capture the dependence between w 1 and w 2

Minimum Description Length (MDL) Principle • Occam’s razor: prefer a simple hypothesis • Simple hypothesis short description length • Minimum description length Bits for encoding data given h hypothesis h • LC (x) is the description length for message x under coding scheme c
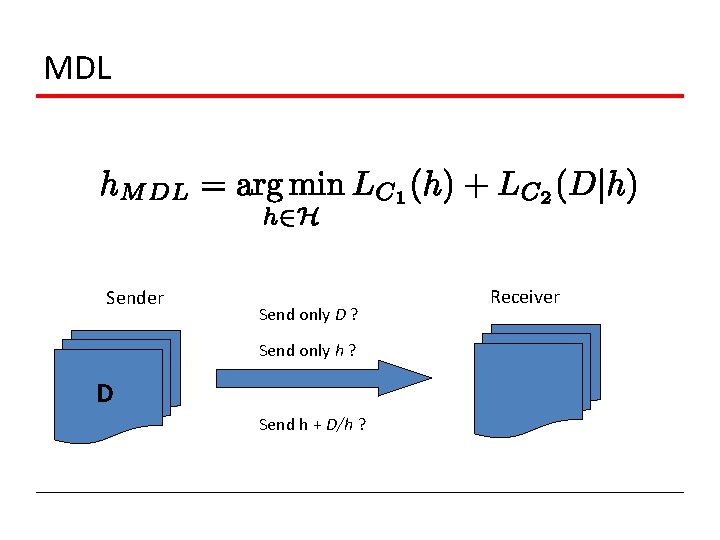
MDL Sender Send only D ? Send only h ? D Send h + D/h ? Receiver

Example: Decision Tree H = decision trees, D = training data labels • LC 1(h) is # bits to describe tree h • LC 2(D|h) is # bits to describe D given tree h • LC 2(D|h)=0 if examples are classified perfectly by h. • Only need to describe exceptions h. MDL trades off tree size for training errors
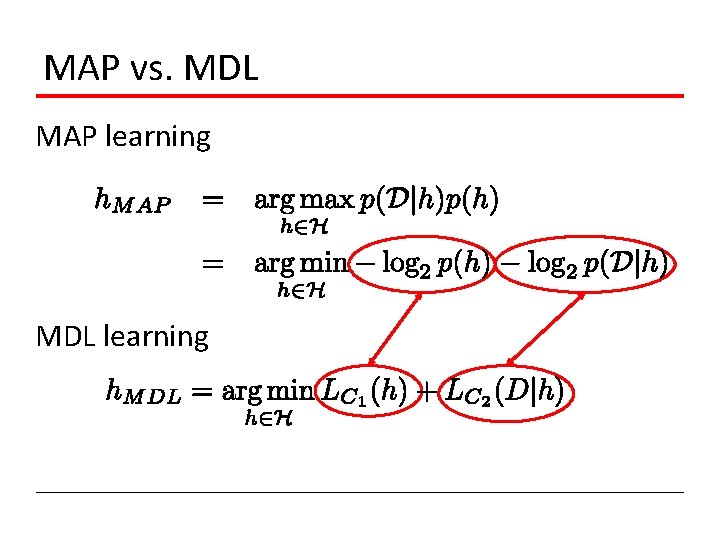
MAP vs. MDL MAP learning MDL learning

Problems with Maximum Approaches Consider Three possible hypotheses: Maximum approaches will pick h 1 Given new instance x Maximum approaches will output + However, is this most probable result?

Bayes Optimal Classifier (Bayesian Average) Bayes optimal classification: Example: The most probable class is -

Computational Issues • Need to sum over all possible hypotheses • It is expensive or impossible when the hypothesis space is large • E. g. , decision tree • Solution: sampling !

Gibbs Classifier Gibbs algorithm 1. Choose one hypothesis at random, according to p(h|D) 2. Use this hypothesis to classify new instance • Surprising fact: • Improve by sampling multiple hypotheses from p(h|D) and average their classification results

Bagging Classifiers In general, sampling from p(h|D) is difficult • • • P(h|D) is difficult to compute P(h|D) is impossible to compute for nonprobabilistic classifier such as SVM Bagging Classifiers: • • Realize sampling p(h|D) by sampling training examples

Boostrap Sampling Bagging = Boostrap aggregating • Boostrap sampling: given set D containing m training examples • Create Di by drawing m examples at random with replacement from D • Di expects to leave out about 0. 37 of examples from D

Bagging Algorithm • Create k boostrap samples D 1, D 2, …, Dk • Train distinct classifier hi on each Di • Classify new instance by classifier vote with equal weights
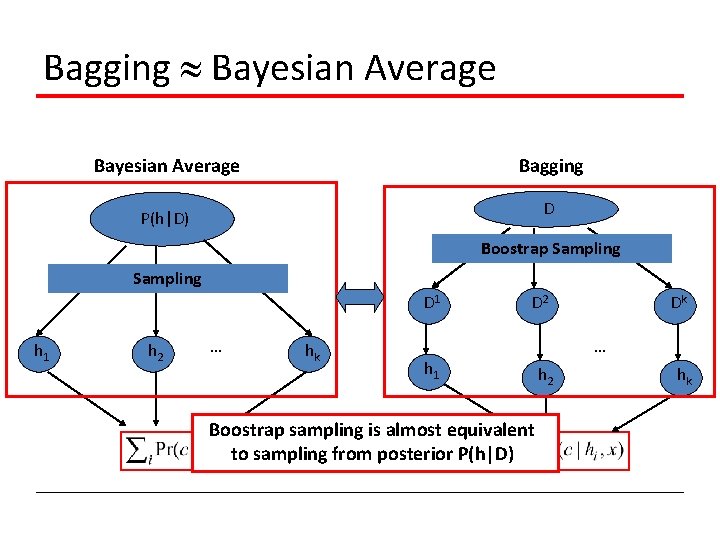
Bagging Bayesian Average Bagging D P(h|D) Boostrap Sampling D 1 h 2 … hk D 2 Dk … h 1 Boostrap sampling is almost equivalent to sampling from posterior P(h|D) h 2 hk
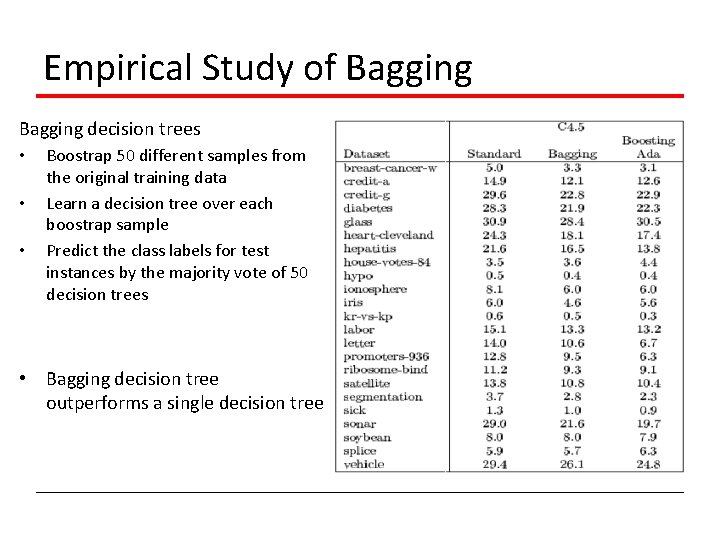
Empirical Study of Bagging decision trees • • • Boostrap 50 different samples from the original training data Learn a decision tree over each boostrap sample Predict the class labels for test instances by the majority vote of 50 decision trees • Bagging decision tree outperforms a single decision tree
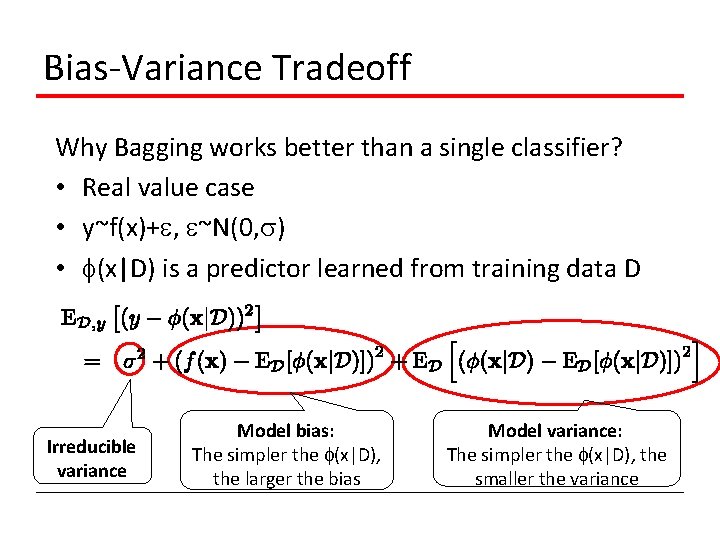
Bias-Variance Tradeoff Why Bagging works better than a single classifier? • Real value case • y~f(x)+ , ~N(0, ) • (x|D) is a predictor learned from training data D Irreducible variance Model bias: The simpler the (x|D), the larger the bias Model variance: The simpler the (x|D), the smaller the variance
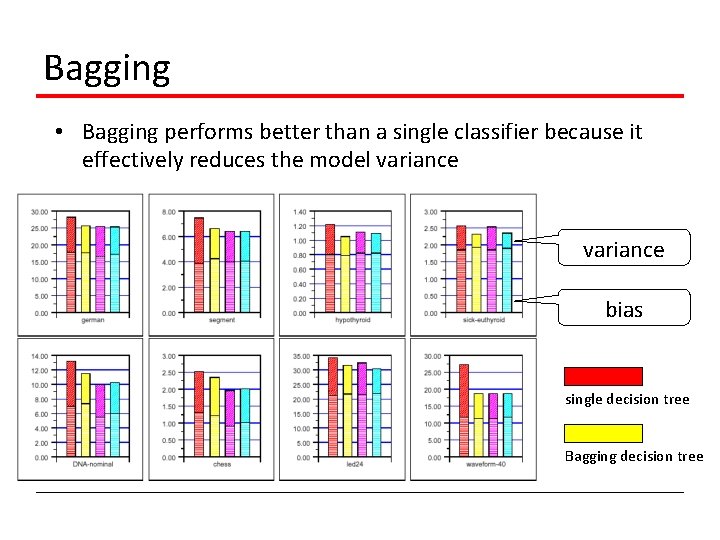
Bagging • Bagging performs better than a single classifier because it effectively reduces the model variance bias single decision tree Bagging decision tree
- Slides: 24