Bayesian inference of binomial problem Estimating a probability

Bayesian inference of binomial problem • Estimating a probability from binomial data – Objective is to estimate unknown proportion (or probability of success, i. e. , to get 1) from Bernoulli trials data y 1, y 2, …, yn that consists of either 0 or 1. – Let the parameter q be the proportion of success in the population, or equivalently probability of success. – Then the probability to obtain y number of successes in n trials which is called binomial distribution. This is discrete function w. r. t. y. • Practice y = 0: 10; n=10; p=0. 5; pmf = nchoosek(n, y)*p^y*(1 -p)^(n-y); y = 0: 10; n=10; p=0. 5; pmf = binopdf(y, n, p); plot(y, pmf, '+') -1 -

Bayesian inference of binomial problem • Inference problem statement – – Let the parameter q be the proportion of females in the population. Current accepted value in Europe is 0. 485, less than 0. 5. Estimate q conditional on the observed data: y females out of n births. Simplest way is just to let q = y/n. • Bayesian inference – Assume non-informative prior: q ~ uniform on [0, 1]. – Likelihood: – Posterior density: -2 -

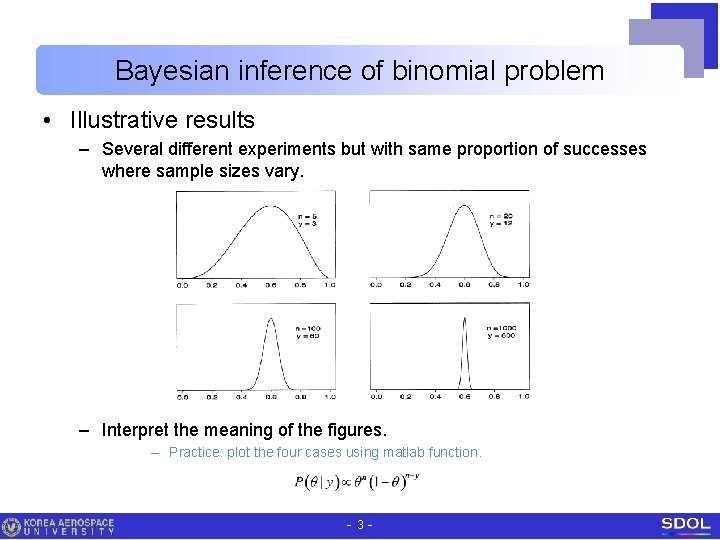
Bayesian inference of binomial problem • Illustrative results – Several different experiments but with same proportion of successes where sample sizes vary. – Interpret the meaning of the figures. – Practice: plot the four cases using matlab function. -3 -

Bayesian inference of binomial problem • Beta pdf – In fact, the posterior density is beta distribution with parameters a = y+1, b = n-y+1. – Practice : plot the four cases using beta pdf function. • Laplace in 18 th Century – 241, 945 girls, 251, 527 boys in Paris during 1745 ~ 1770. – P[q ≥ 0. 5 | y] ≈ 1. 15 10 -42 So he was ‘certain’ that q < 0. 5. – Practice: calculate this value, and validate. • Posterior prediction – What is the probability to get girl if a new baby born ? – Practice: calculate this value. What if the numbers were 2 out of 5 ? -4 -

Bayesian inference of binomial problem • Summarizing posterior inference – Locations summary: • • Mean: expectation, needs integration. Mode: most-likely value. Maximum of pdf. Needs optimization or d(pdf)/dx. Median: 50% percentile value. Among these, mode is preferred due to the computational convenience. – Variations summary: • Standard deviation or variance • Interquartile range or 100(1 -a)% interval – Practice with beta pdf. Mean, mode are given as equation analytically. Others are obtained using matlab functions. – In general, these values are computed using computer simulations from the posterior distribution. -5 -

Bayesian inference of binomial problem • Informative prior – So far considered only uniform prior. – Recall the likelihood is binomial pdf: – Let us introduce prior of beta pdf: where a, b are called hyperparameters. – Then posterior density: • Remarks – Property that posterior distribution follows same form as the prior is called conjugacy. Beta prior is conjugate family of binomial likelihood. – As a result, the mean & variance of posterior pdf: – As y & n-y become large under fixed a & b, In the limit, parameters of the prior have no influence on posterior. Besides, it converges to normal pdf due to central limit theorem. -6 -

Homework • 2. 5 example: estimating probability of female birth – P[ q < 0. 485 ] – Histogram of posterior pdf q|y – Median and 95% confidence intervals. Ans. 446, [. 415, . 477] -7 -