Bayesian Inference Lee Harrison York Neuroimaging Centre 14

Bayesian Inference Lee Harrison York Neuroimaging Centre 14 / 05 / 2010
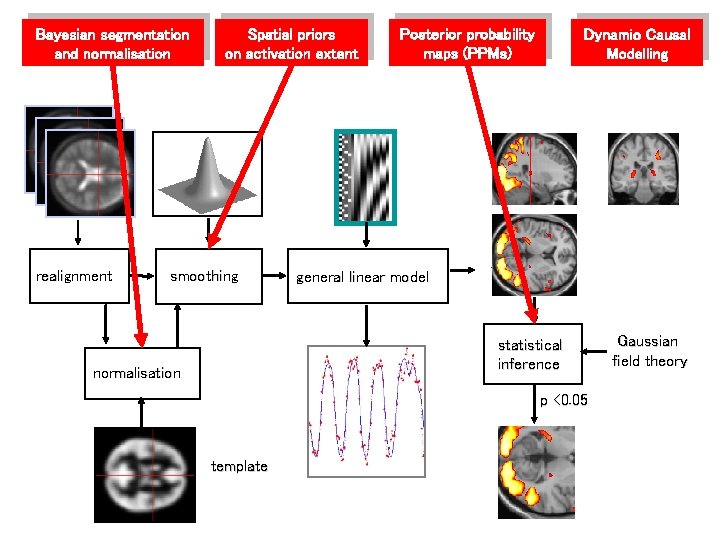
Bayesian segmentation and normalisation realignment Spatial priors on activation extent smoothing Posterior probability maps (PPMs) Dynamic Causal Modelling general linear model statistical inference normalisation p <0. 05 template Gaussian field theory
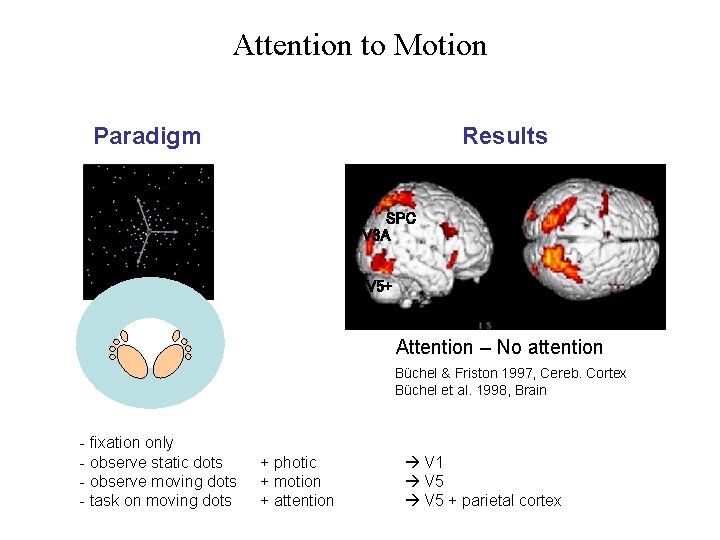
Attention to Motion Paradigm Results SPC V 3 A V 5+ Attention – No attention Büchel & Friston 1997, Cereb. Cortex Büchel et al. 1998, Brain - fixation only - observe static dots - observe moving dots - task on moving dots + photic + motion + attention V 1 V 5 + parietal cortex
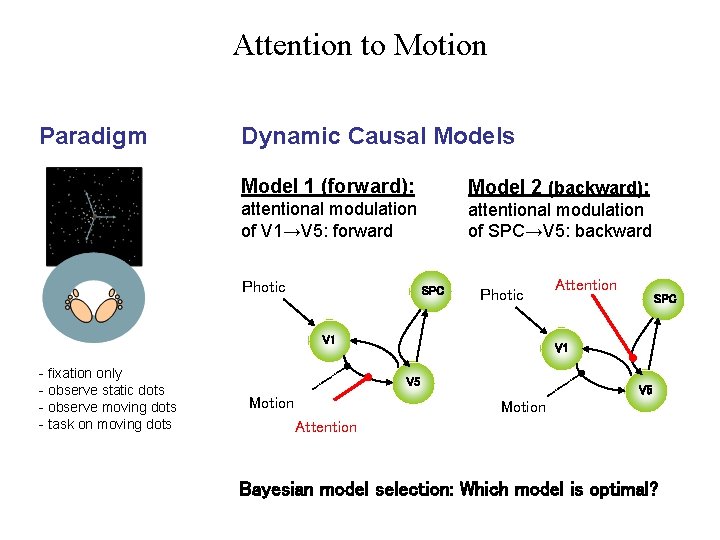
Attention to Motion Paradigm Dynamic Causal Models Model 1 (forward): Model 2 (backward): attentional modulation of V 1→V 5: forward attentional modulation of SPC→V 5: backward Photic SPC Photic V 1 - fixation only - observe static dots - observe moving dots - task on moving dots SPC V 1 V 5 Motion Attention Bayesian model selection: Which model is optimal?

Responses to Uncertainty Long term memory Short term memory
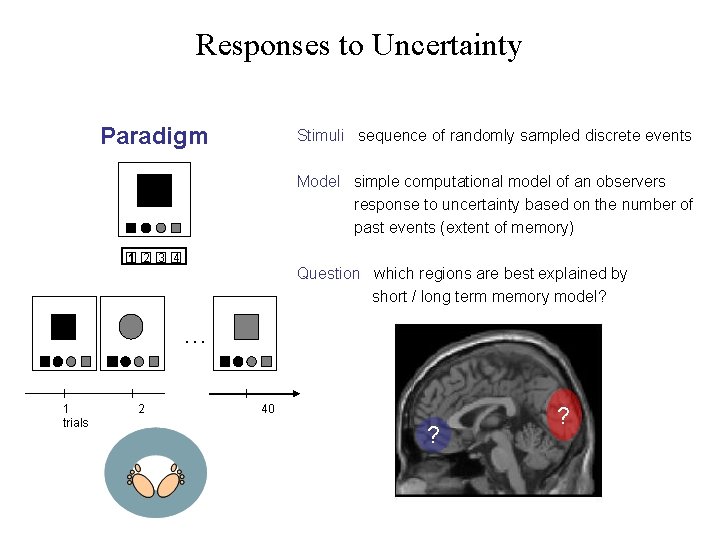
Responses to Uncertainty Paradigm Stimuli sequence of randomly sampled discrete events Model simple computational model of an observers response to uncertainty based on the number of past events (extent of memory) 1 2 3 4 Question which regions are best explained by short / long term memory model? … 1 trials 2 40 ? ?

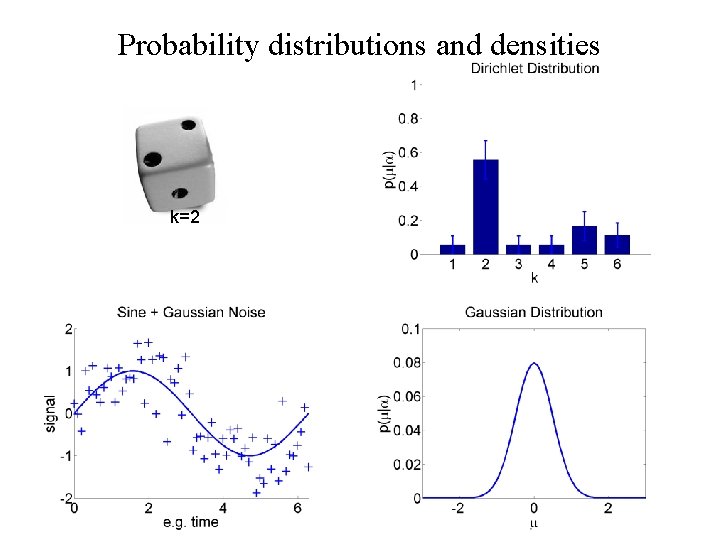
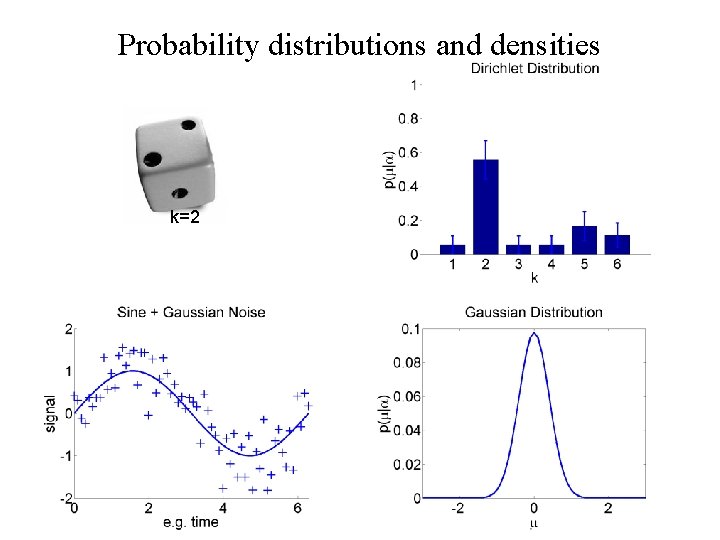
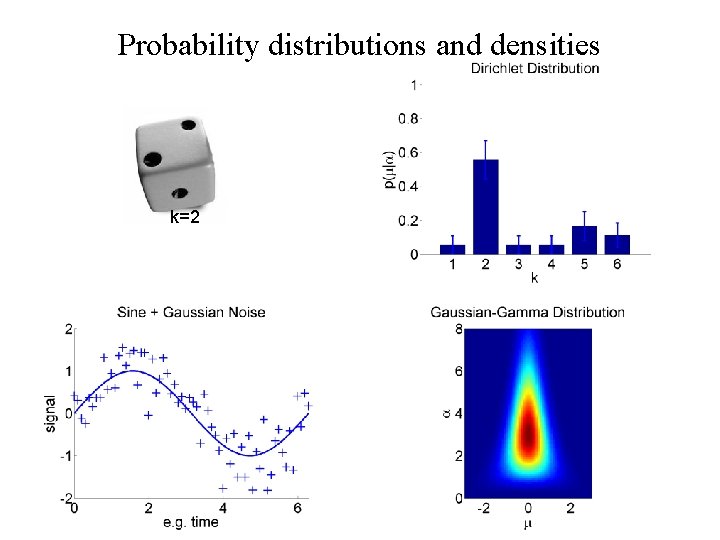
Overview • Introductory remarks • Some probability densities/distributions • Probabilistic (generative) models • Bayesian inference • A simple example – Bayesian linear regression • SPM applications – Segmentation – Dynamic causal modeling – Spatial models of f. MRI time series
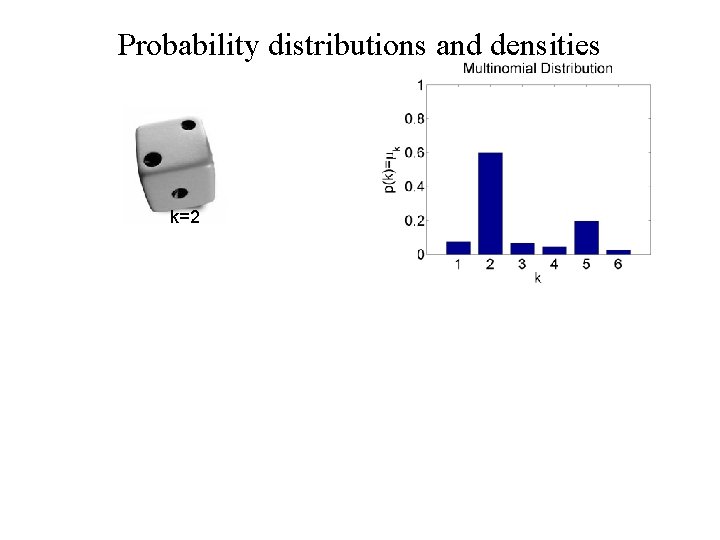
Probability distributions and densities k=2
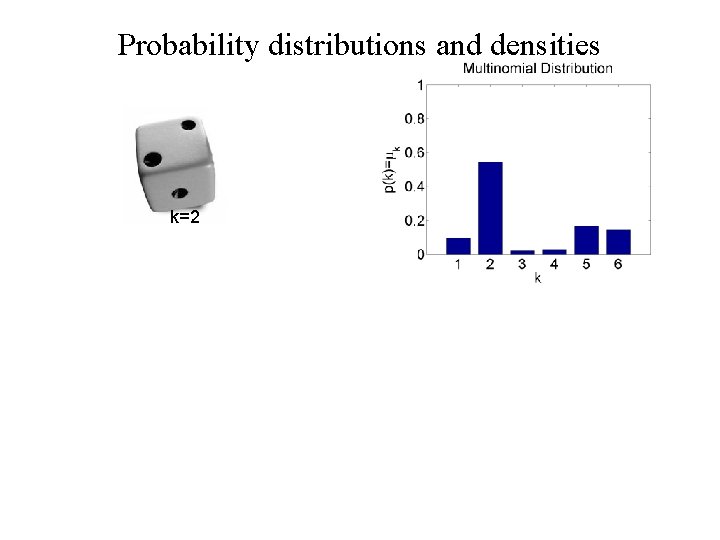
Probability distributions and densities k=2
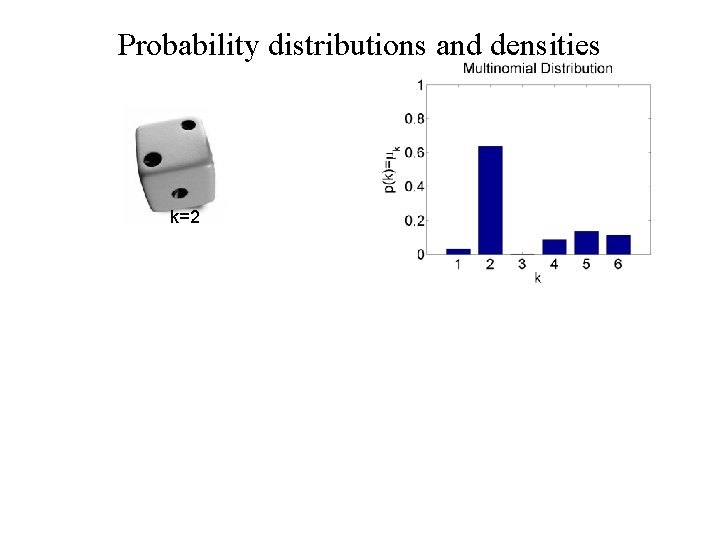
Probability distributions and densities k=2
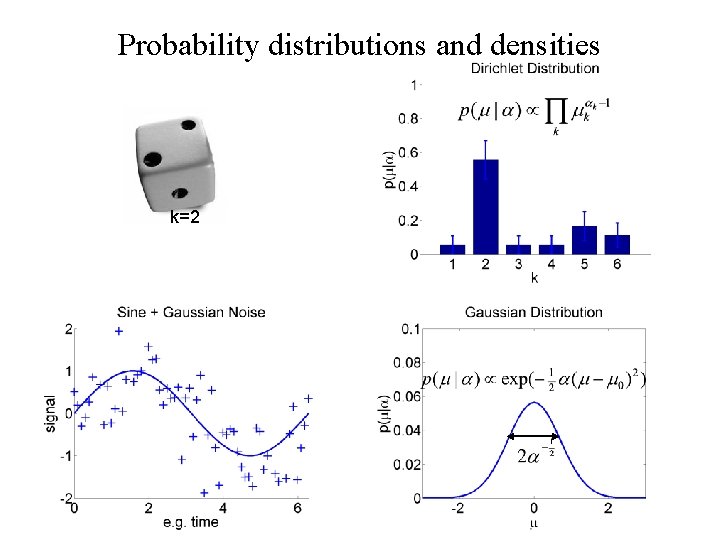
Probability distributions and densities k=2
Probability distributions and densities k=2
Probability distributions and densities k=2
Probability distributions and densities k=2
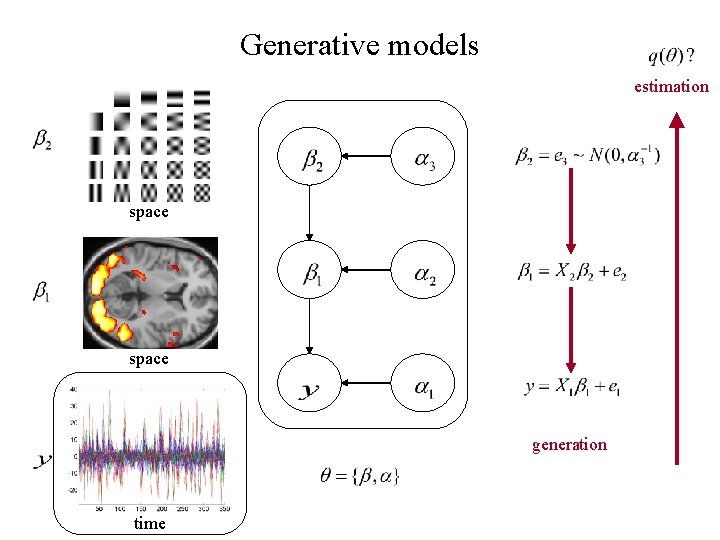
Generative models estimation space generation time
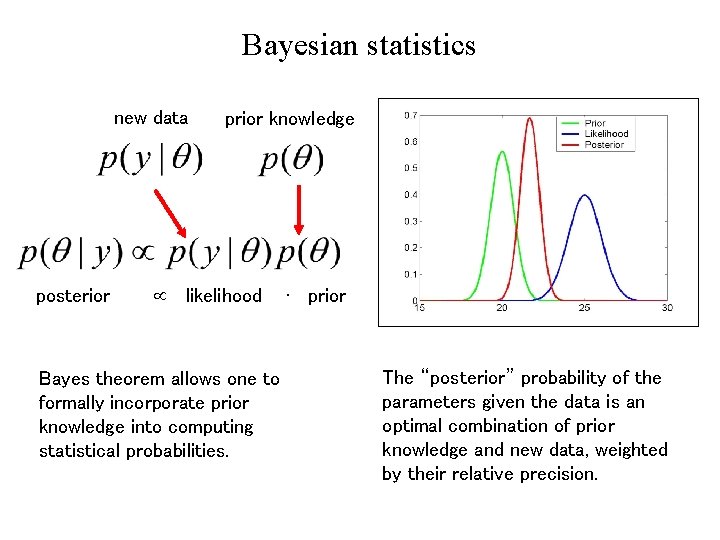
Bayesian statistics new data posterior prior knowledge likelihood Bayes theorem allows one to formally incorporate prior knowledge into computing statistical probabilities. ∙ prior The “posterior” probability of the parameters given the data is an optimal combination of prior knowledge and new data, weighted by their relative precision.
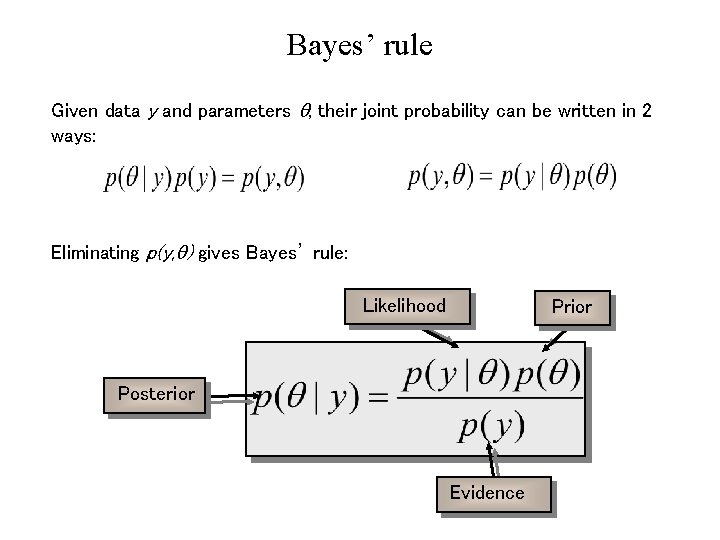
Bayes’ rule Given data y and parameters , their joint probability can be written in 2 ways: Eliminating p(y, ) gives Bayes’ rule: Likelihood Prior Posterior Evidence

Principles of Bayesian inference ð Formulation of a generative model likelihood p(y| ) prior distribution p( ) ð Observation of data y ð Update of beliefs based upon observations, given a prior state of knowledge
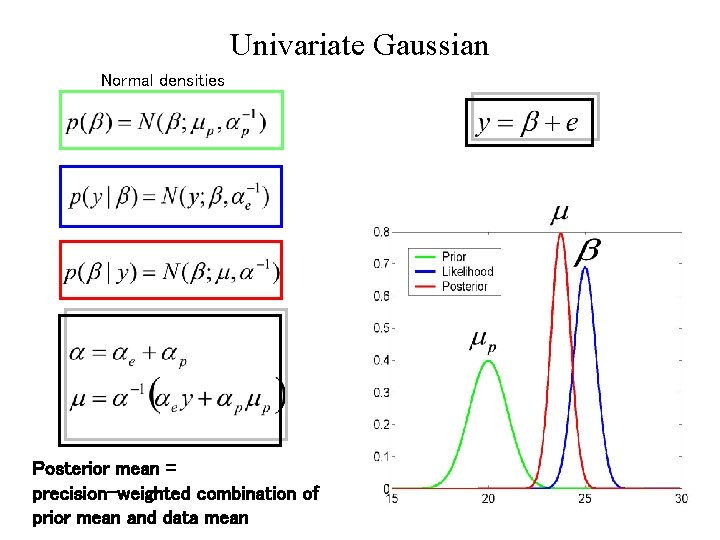
Univariate Gaussian Normal densities Posterior mean = precision-weighted combination of prior mean and data mean

Bayesian GLM: univariate case Normal densities

Bayesian GLM: multivariate case β 2 Normal densities One step if Ce and Cp are known. Otherwise iterative estimation. β 1
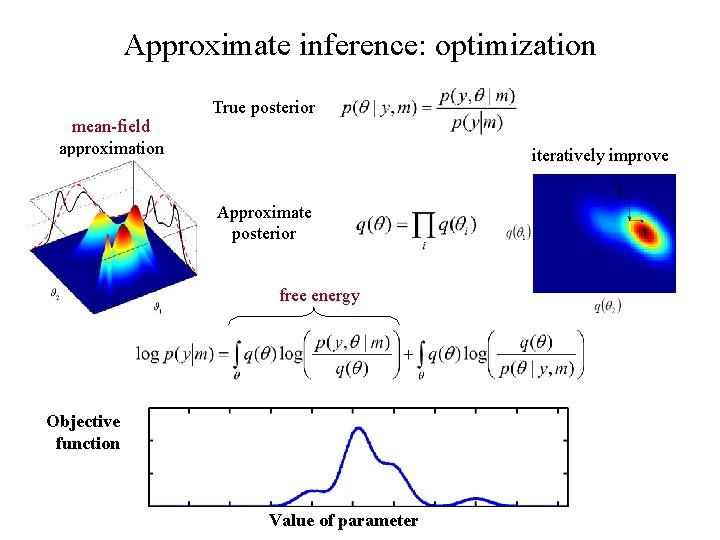
Approximate inference: optimization mean-field approximation True posterior iteratively improve Approximate posterior free energy Objective function Value of parameter

Simple example – linear regression Data Ordinary least squares
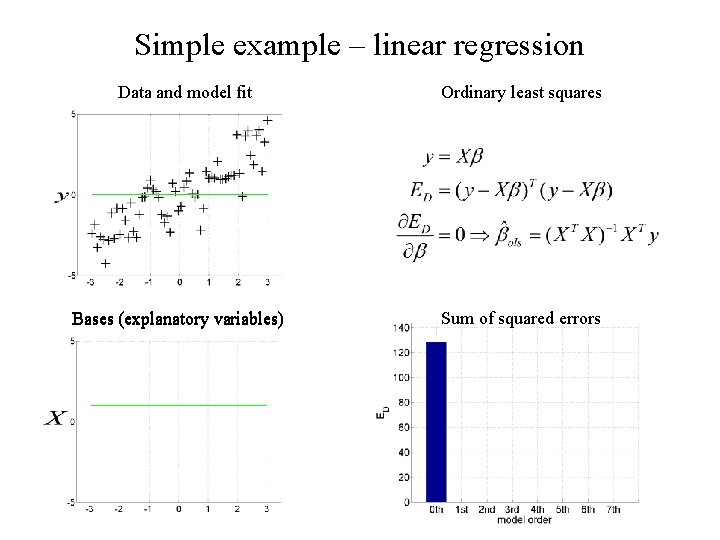
Simple example – linear regression Data and model fit Bases (explanatory variables) Ordinary least squares Sum of squared errors
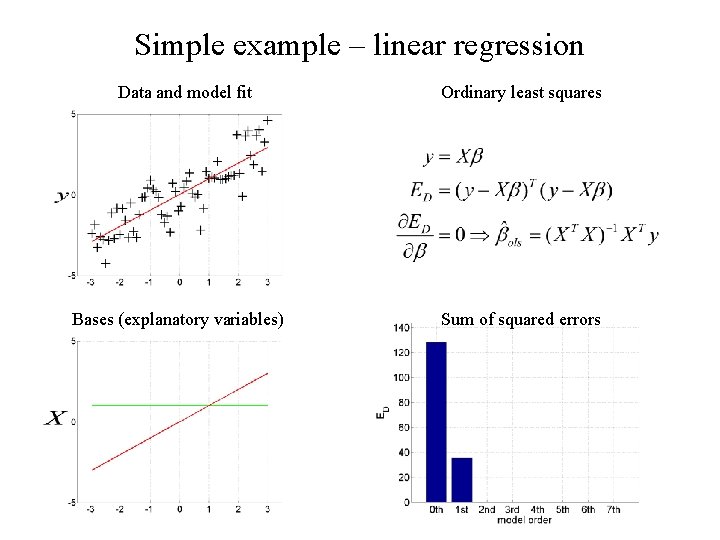
Simple example – linear regression Data and model fit Bases (explanatory variables) Ordinary least squares Sum of squared errors
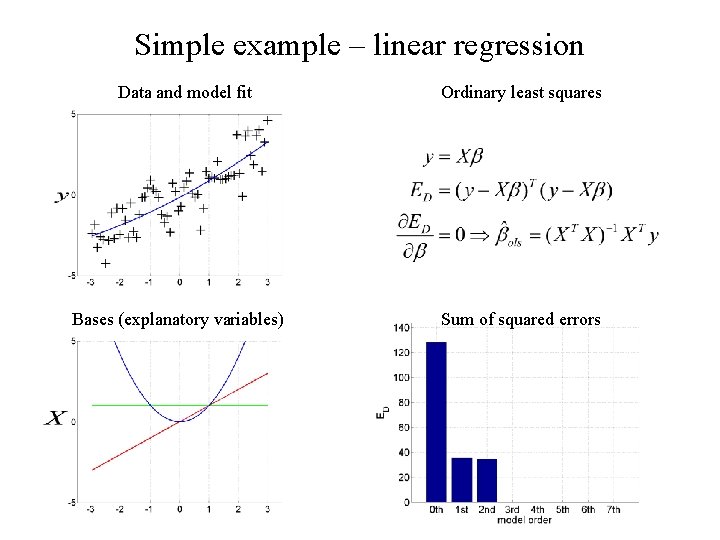
Simple example – linear regression Data and model fit Bases (explanatory variables) Ordinary least squares Sum of squared errors
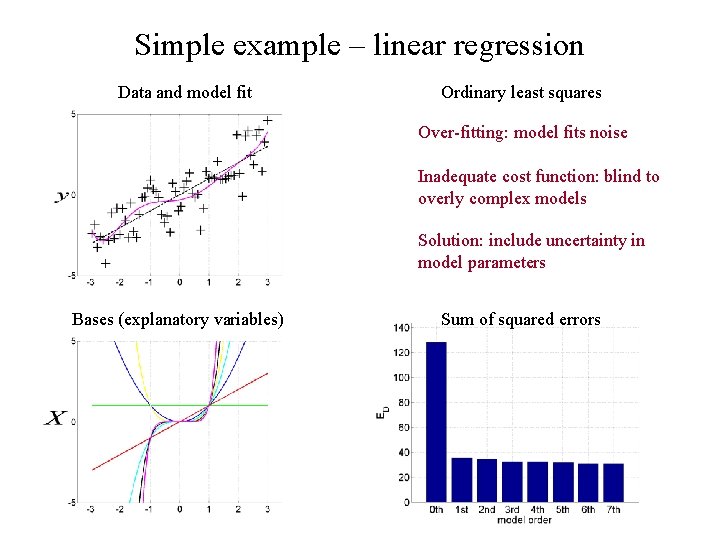
Simple example – linear regression Data and model fit Ordinary least squares Over-fitting: model fits noise Inadequate cost function: blind to overly complex models Solution: include uncertainty in model parameters Bases (explanatory variables) Sum of squared errors

Bayesian linear regression: priors and likelihood Model:
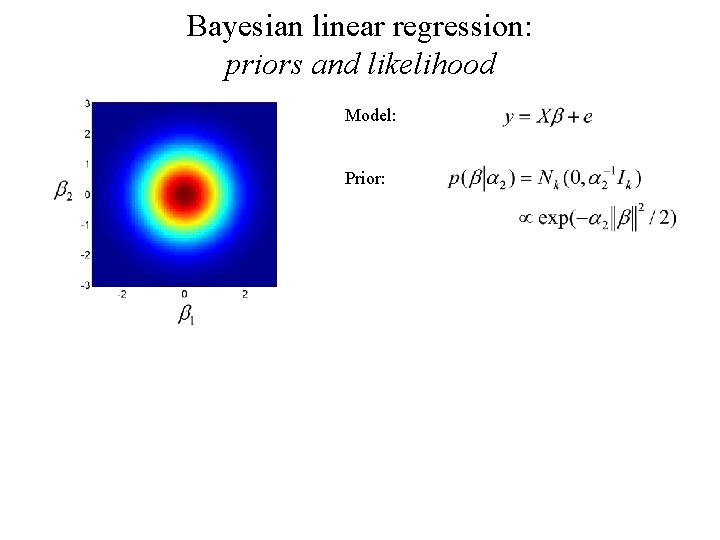
Bayesian linear regression: priors and likelihood Model: Prior:
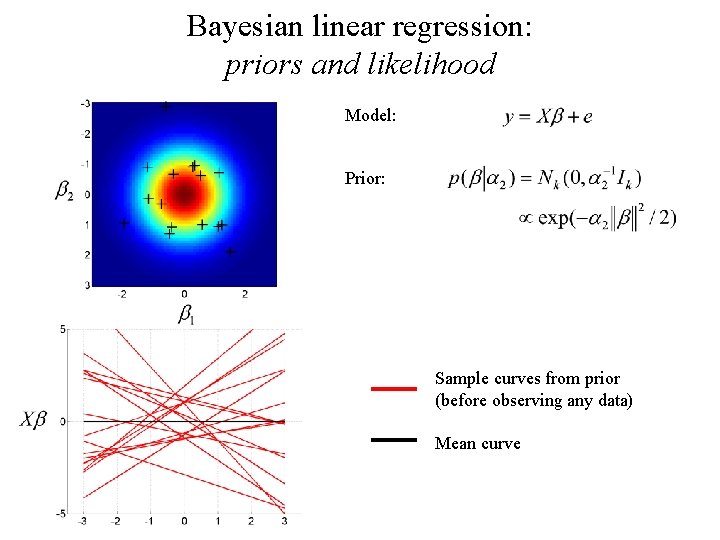
Bayesian linear regression: priors and likelihood Model: Prior: Sample curves from prior (before observing any data) Mean curve
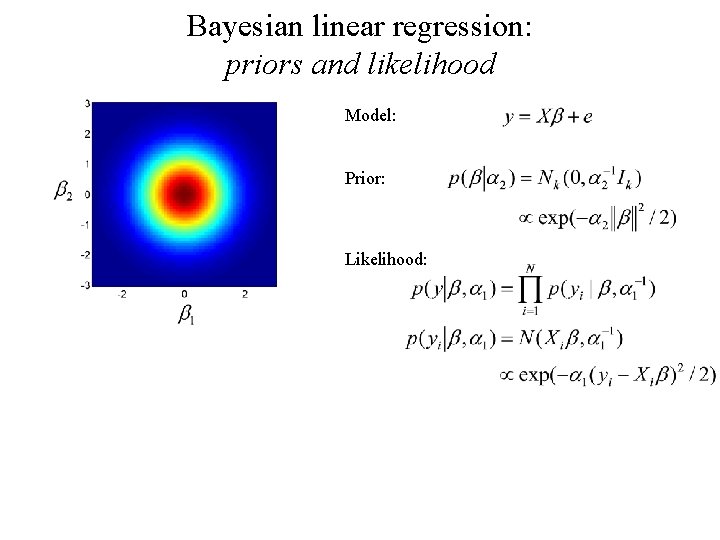
Bayesian linear regression: priors and likelihood Model: Prior: Likelihood:
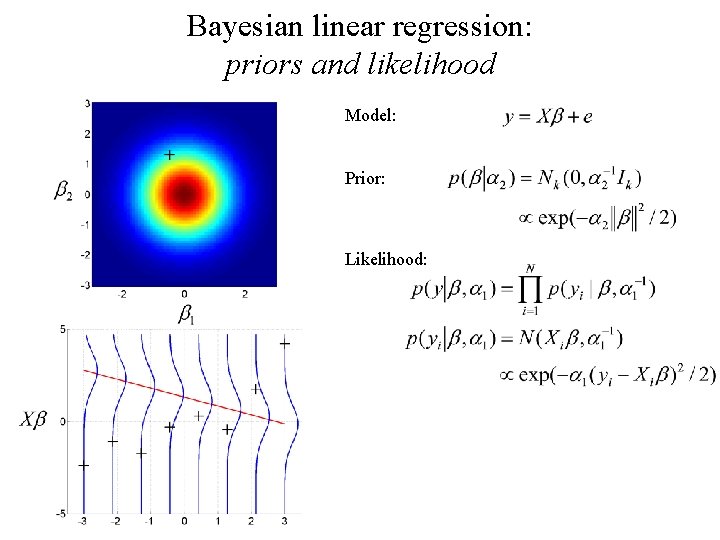
Bayesian linear regression: priors and likelihood Model: Prior: Likelihood:
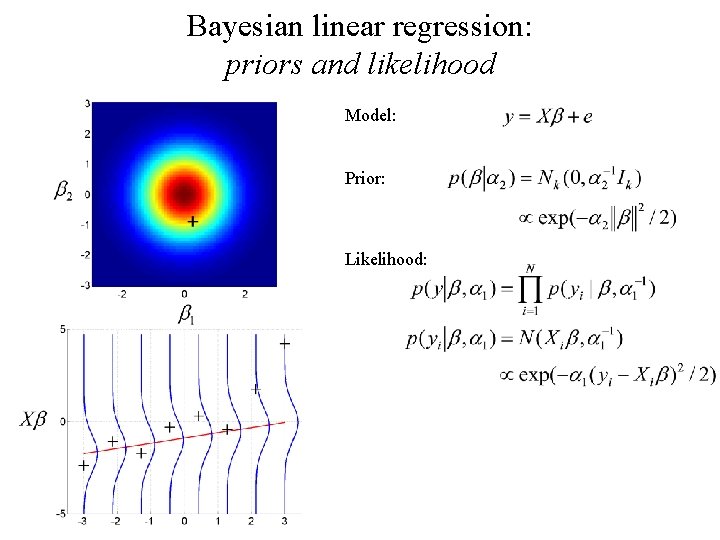
Bayesian linear regression: priors and likelihood Model: Prior: Likelihood:

Bayesian linear regression: posterior Model: Prior: Likelihood: Bayes Rule:
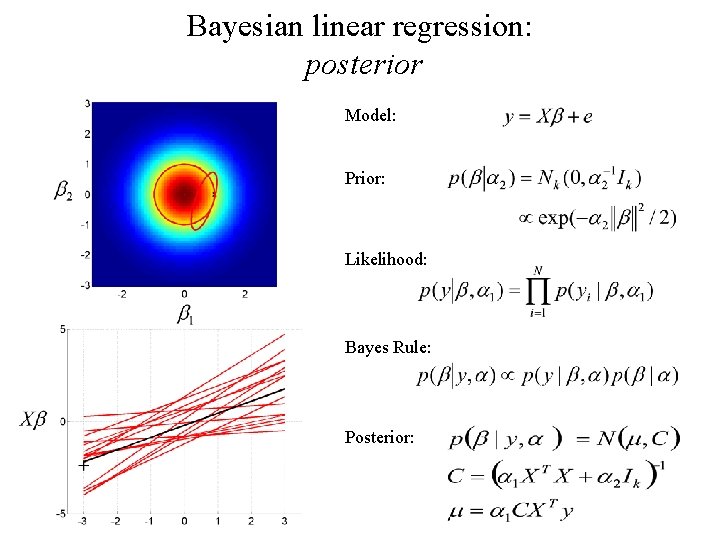
Bayesian linear regression: posterior Model: Prior: Likelihood: Bayes Rule: Posterior:
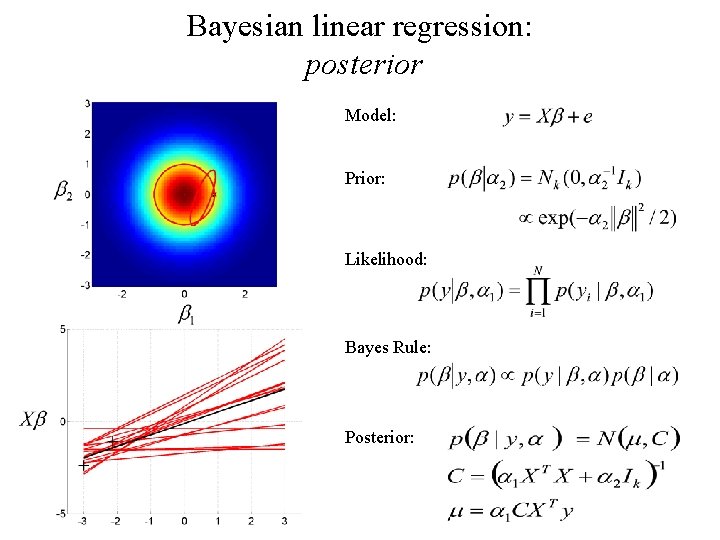
Bayesian linear regression: posterior Model: Prior: Likelihood: Bayes Rule: Posterior:
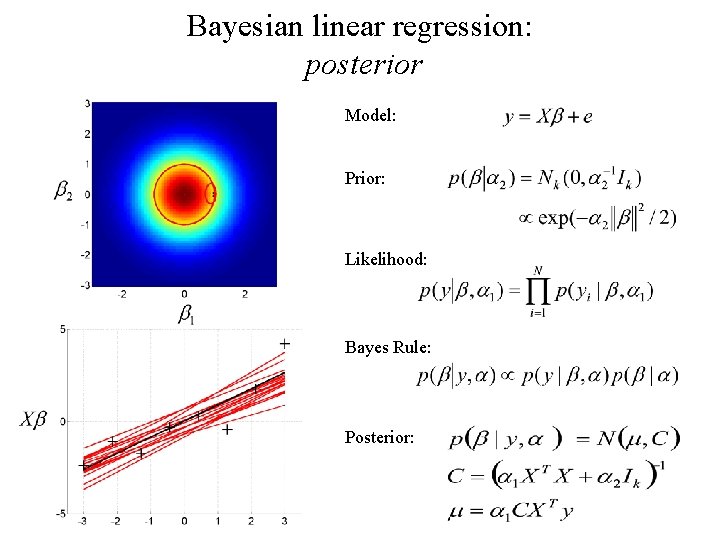
Bayesian linear regression: posterior Model: Prior: Likelihood: Bayes Rule: Posterior:

Posterior Probability Maps (PPMs) Posterior distribution: probability of the effect given the data mean: size of effect precision: variability Posterior probability map: images of the probability (confidence) that an activation exceeds some specified threshold sth, given the data y Two thresholds: • activation threshold sth : percentage of whole brain mean signal (physiologically relevant size of effect) • probability pth that voxels must exceed to be displayed (e. g. 95%)

Bayesian linear regression: model selection Bayes Rule: normalizing constant Model evidence:
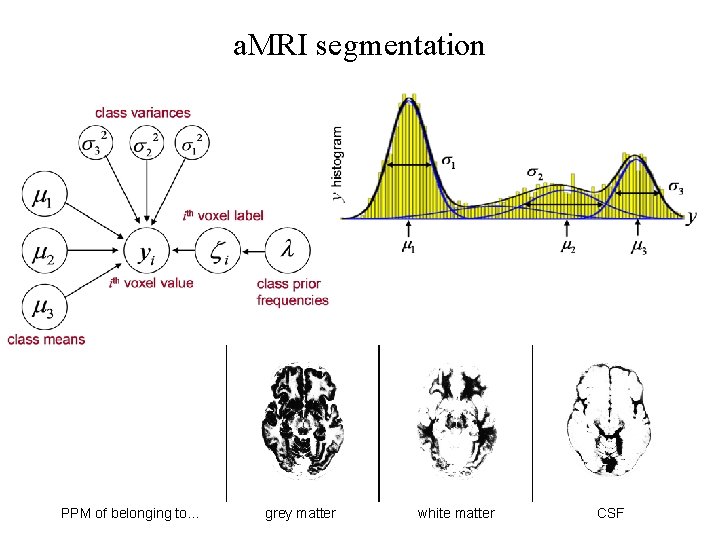
a. MRI segmentation PPM of belonging to… grey matter white matter CSF
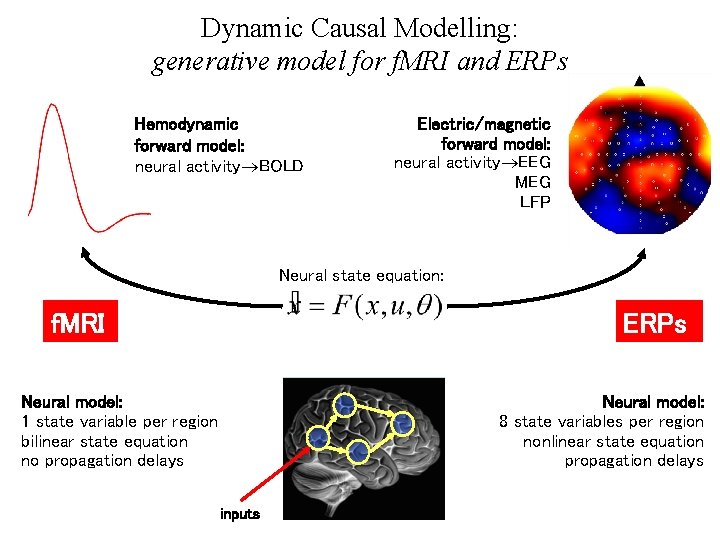
Dynamic Causal Modelling: generative model for f. MRI and ERPs Hemodynamic forward model: neural activity BOLD Electric/magnetic forward model: neural activity EEG MEG LFP Neural state equation: f. MRI ERPs Neural model: 1 state variable per region bilinear state equation no propagation delays Neural model: 8 state variables per region nonlinear state equation propagation delays inputs
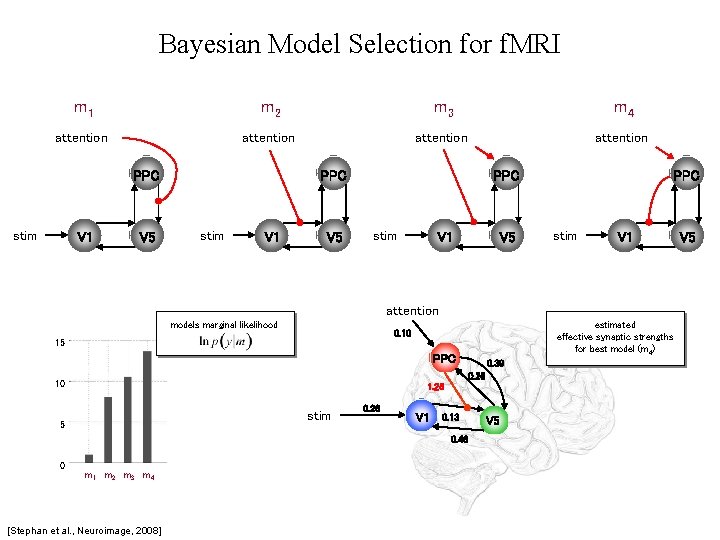
Bayesian Model Selection for f. MRI m 1 m 2 m 3 m 4 attention PPC stim V 1 V 5 PPC stim V 1 attention models marginal likelihood estimated effective synaptic strengths for best model (m 4) 0. 10 15 PPC 10 1. 25 stim 5 0. 26 V 1 0. 13 0. 46 0 0. 39 0. 26 m 1 m 2 m 3 m 4 [Stephan et al. , Neuroimage, 2008] V 5
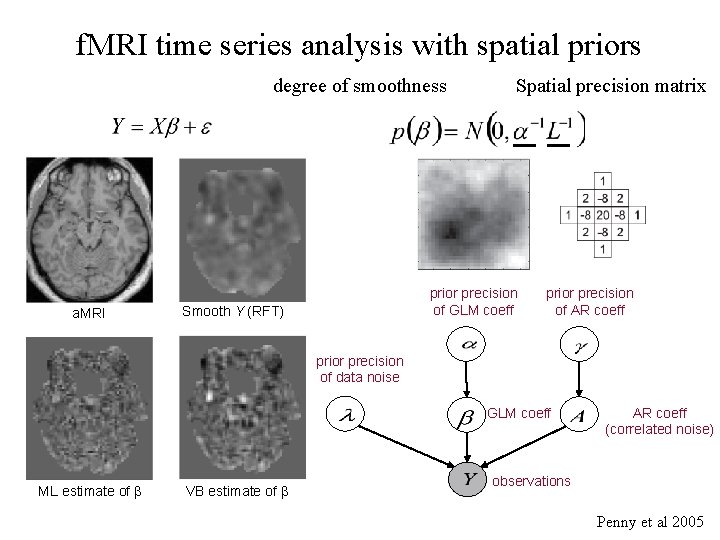
f. MRI time series analysis with spatial priors degree of smoothness a. MRI Spatial precision matrix prior precision of GLM coeff Smooth Y (RFT) prior precision of AR coeff prior precision of data noise GLM coeff ML estimate of β VB estimate of β AR coeff (correlated noise) observations Penny et al 2005
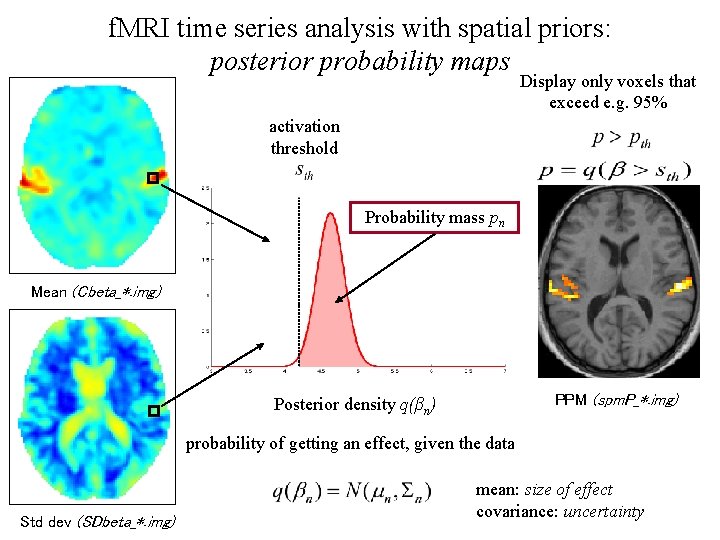
f. MRI time series analysis with spatial priors: posterior probability maps Display only voxels that exceed e. g. 95% activation threshold Probability mass pn Mean (Cbeta_*. img) PPM (spm. P_*. img) Posterior density q(βn) probability of getting an effect, given the data Std dev (SDbeta_*. img) mean: size of effect covariance: uncertainty
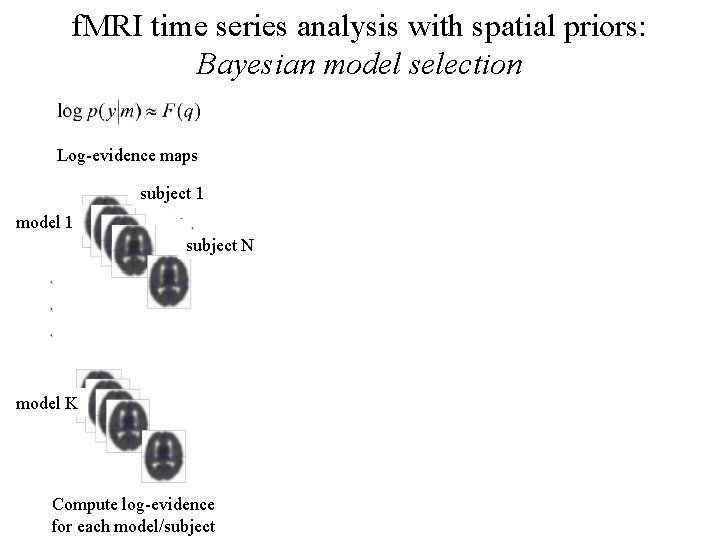
f. MRI time series analysis with spatial priors: Bayesian model selection Log-evidence maps subject 1 model 1 subject N model K Compute log-evidence for each model/subject

f. MRI time series analysis with spatial priors: Bayesian model selection Log-evidence maps BMS maps subject 1 model 1 subject N PPM model K Compute log-evidence for each model/subject EPM Probability that model k generated data model k Joao et al, 2009
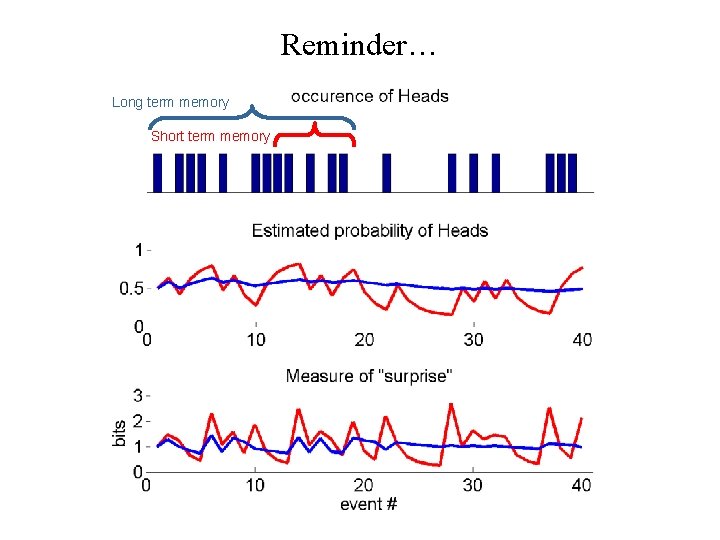
Reminder… Long term memory Short term memory
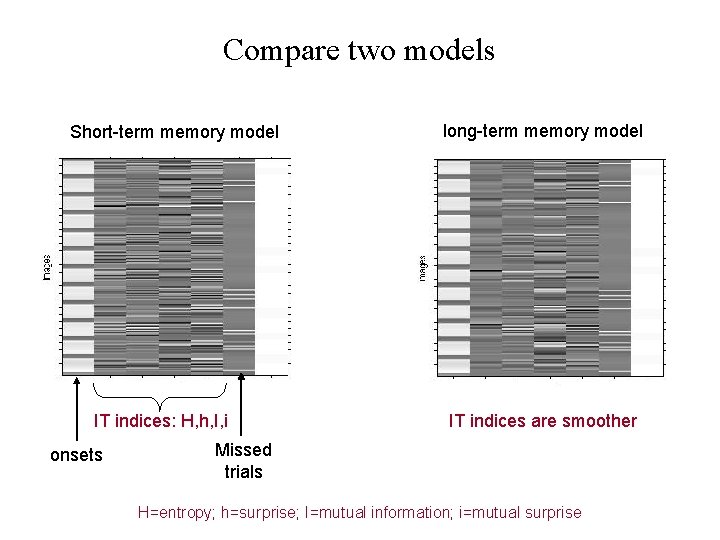
Compare two models Short-term memory model IT indices: H, h, I, i onsets long-term memory model IT indices are smoother Missed trials H=entropy; h=surprise; I=mutual information; i=mutual surprise
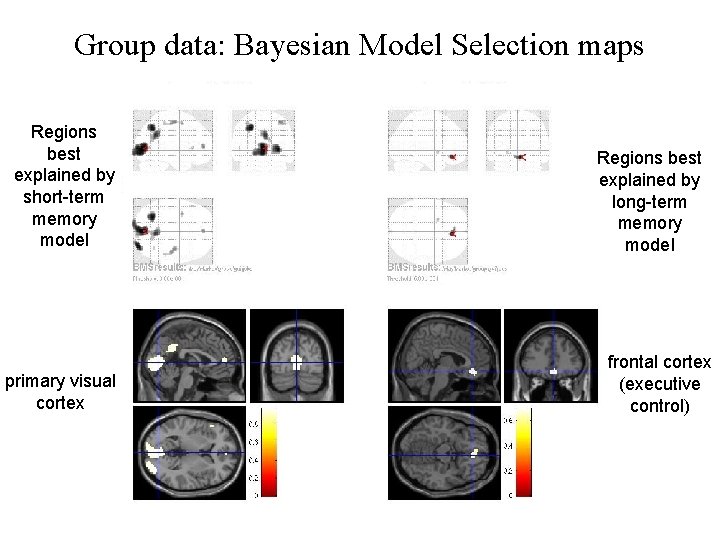
Group data: Bayesian Model Selection maps Regions best explained by short-term memory model primary visual cortex Regions best explained by long-term memory model frontal cortex (executive control)

Thank-you
- Slides: 50