Bayesian inference J Daunizeau Wellcome Trust Centre for

Bayesian inference J. Daunizeau Wellcome Trust Centre for Neuroimaging, London, UK Institute of Empirical Research in Economics, Zurich, Switzerland

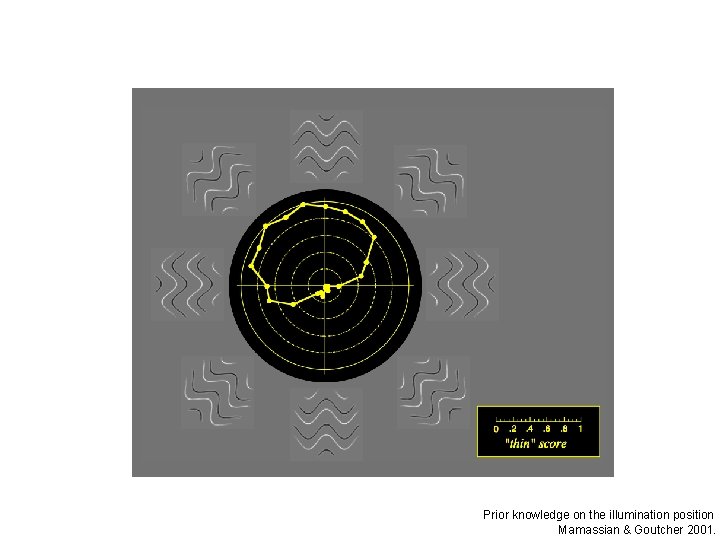
Prior knowledge on the illumination position Mamassian & Goutcher 2001.

Overview of the talk 1 Probabilistic modelling and representation of uncertainty 1. 1 Bayesian paradigm 1. 2 Hierarchical models 1. 3 Frequentist versus Bayesian inference 2 Numerical Bayesian inference methods 2. 1 Sampling methods 2. 2 Variational methods (EM, VB) 3 SPM applications 3. 1 a. MRI segmentation 3. 2 f. MRI time series analysis with spatial priors 3. 3 Dynamic causal modelling 3. 4 EEG source reconstruction 3. 5 Decoding of brain images

Bayesian paradigm theory of probability Degree of plausibility desiderata: - should be represented using real numbers - should conform with intuition - should be consistent • normalization: a=2 • marginalization: a=2 b=5 • conditioning : (Bayes rule) (D 1) (D 2) (D 3)

Bayesian paradigm Likelihood and priors Likelihood: Prior: Bayes rule: generative model m

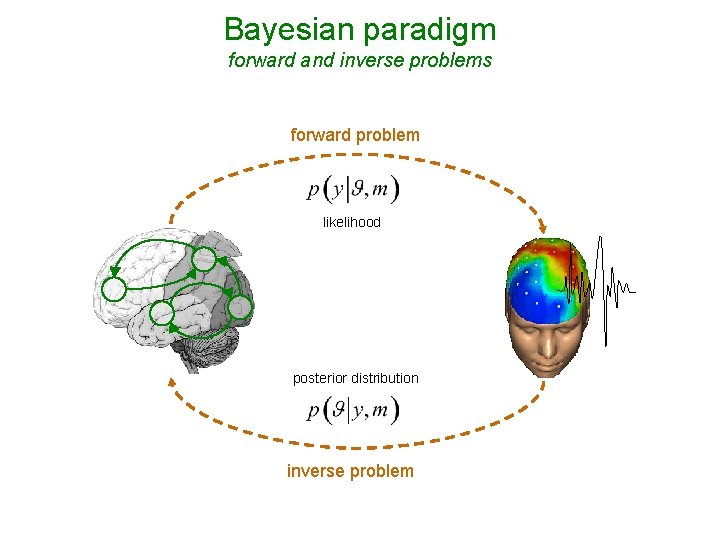
Bayesian paradigm forward and inverse problems forward problem likelihood posterior distribution inverse problem

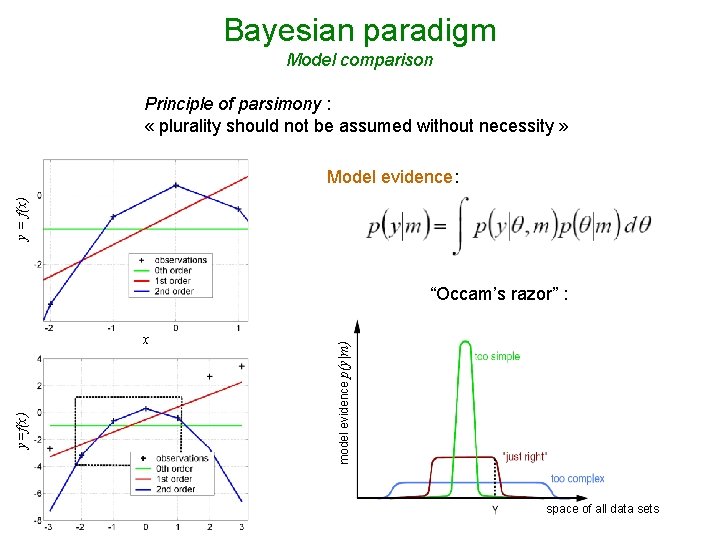
Bayesian paradigm Model comparison Principle of parsimony : « plurality should not be assumed without necessity » y = f(x) Model evidence: y=f(x) x model evidence p(y|m) “Occam’s razor” : space of all data sets

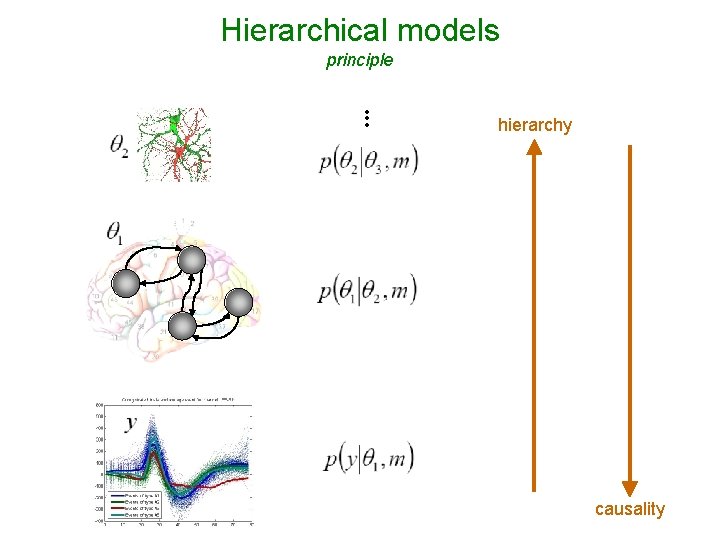
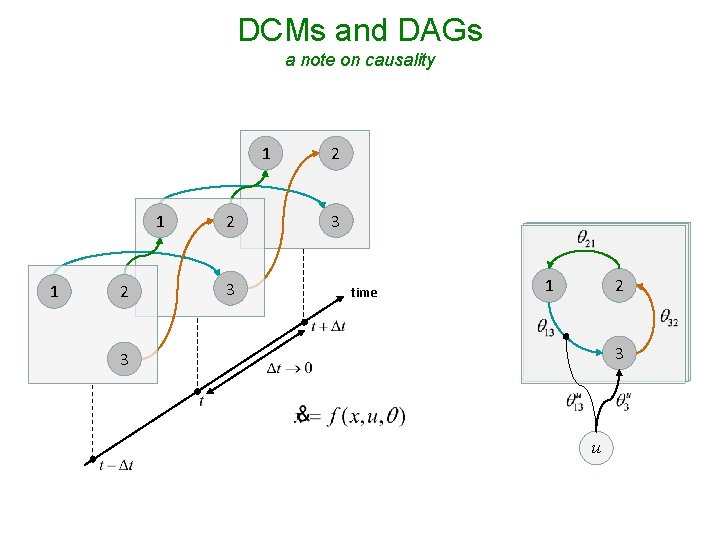
Hierarchical models principle • • • hierarchy causality

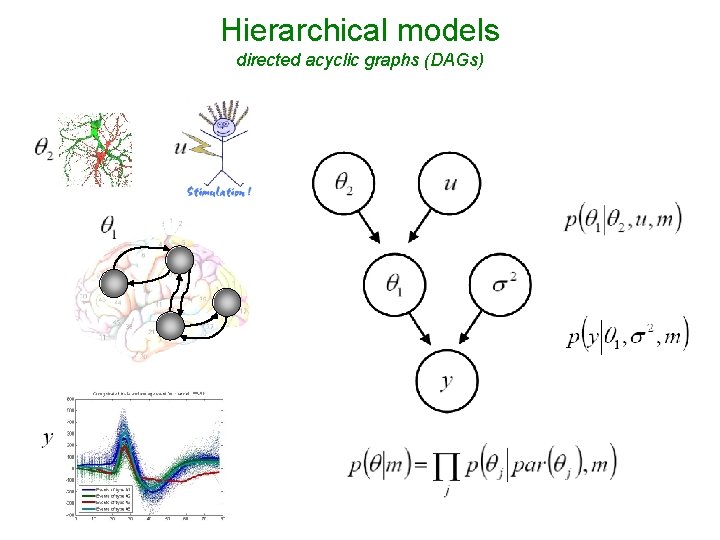
Hierarchical models directed acyclic graphs (DAGs)

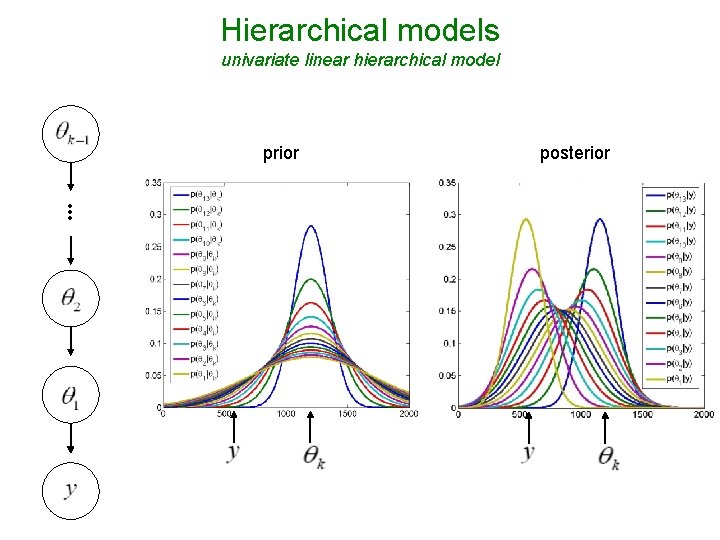
Hierarchical models univariate linear hierarchical model prior posterior • • •

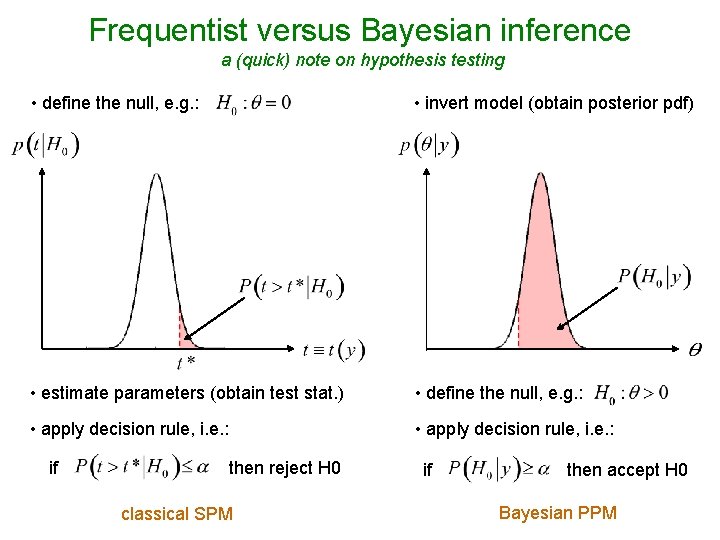
Frequentist versus Bayesian inference a (quick) note on hypothesis testing • define the null, e. g. : • invert model (obtain posterior pdf) • estimate parameters (obtain test stat. ) • define the null, e. g. : • apply decision rule, i. e. : if then reject H 0 classical SPM if then accept H 0 Bayesian PPM

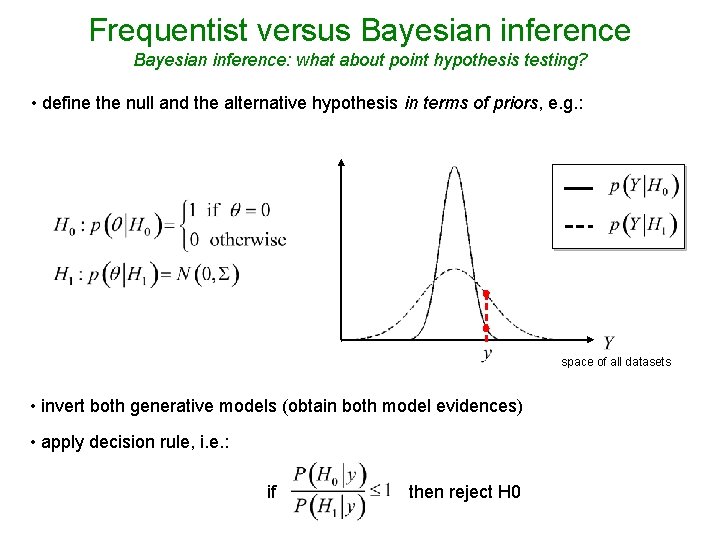
Frequentist versus Bayesian inference: what about point hypothesis testing? • define the null and the alternative hypothesis in terms of priors, e. g. : space of all datasets • invert both generative models (obtain both model evidences) • apply decision rule, i. e. : if then reject H 0

Overview of the talk 1 Probabilistic modelling and representation of uncertainty 1. 1 Bayesian paradigm 1. 2 Hierarchical models 1. 3 Frequentist versus Bayesian inference 2 Numerical Bayesian inference methods 2. 1 Sampling methods 2. 2 Variational methods (EM, VB) 3 SPM applications 3. 1 a. MRI segmentation 3. 2 f. MRI time series analysis with spatial priors 3. 3 Dynamic causal modelling 3. 4 EEG source reconstruction 3. 5 Decoding of brain images

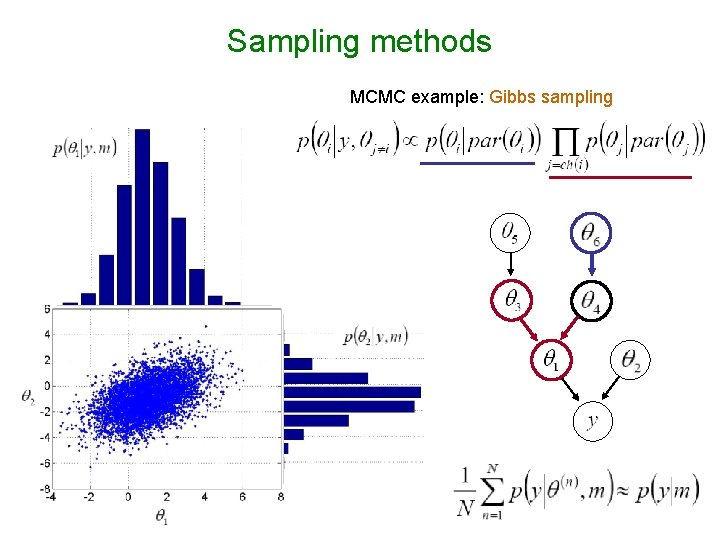
Sampling methods MCMC example: Gibbs sampling

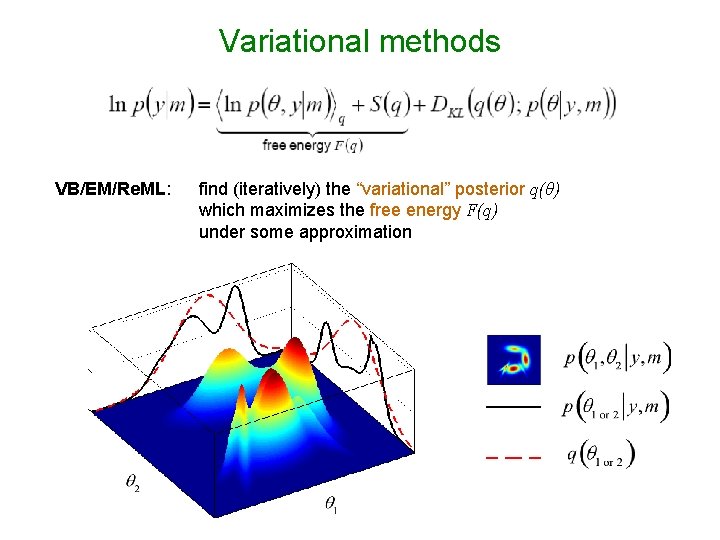
Variational methods VB/EM/Re. ML: find (iteratively) the “variational” posterior q(θ) which maximizes the free energy F(q) under some approximation

Overview of the talk 1 Probabilistic modelling and representation of uncertainty 1. 1 Bayesian paradigm 1. 2 Hierarchical models 1. 3 Frequentist versus Bayesian inference 2 Numerical Bayesian inference methods 2. 1 Sampling methods 2. 2 Variational methods (EM, VB) 3 SPM applications 3. 1 a. MRI segmentation 3. 2 f. MRI time series analysis with spatial priors 3. 3 Dynamic causal modelling 3. 4 EEG source reconstruction 3. 5 Decoding of brain images

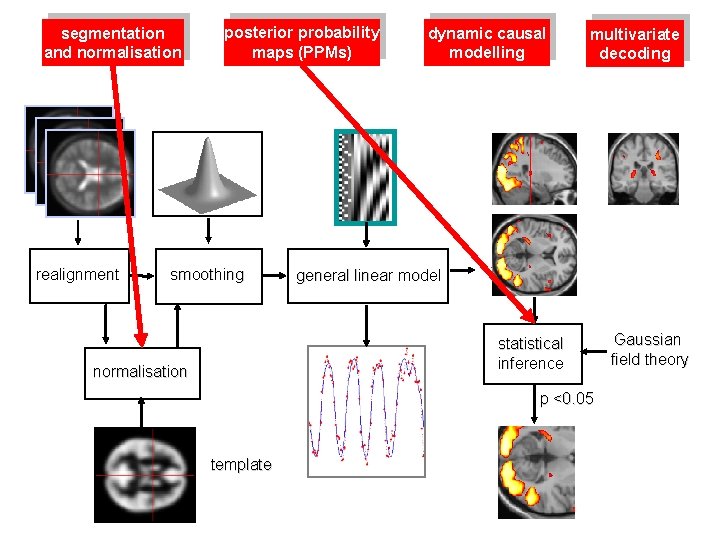
segmentation and normalisation realignment posterior probability maps (PPMs) smoothing dynamic causal modelling multivariate decoding general linear model statistical inference normalisation p <0. 05 template Gaussian field theory

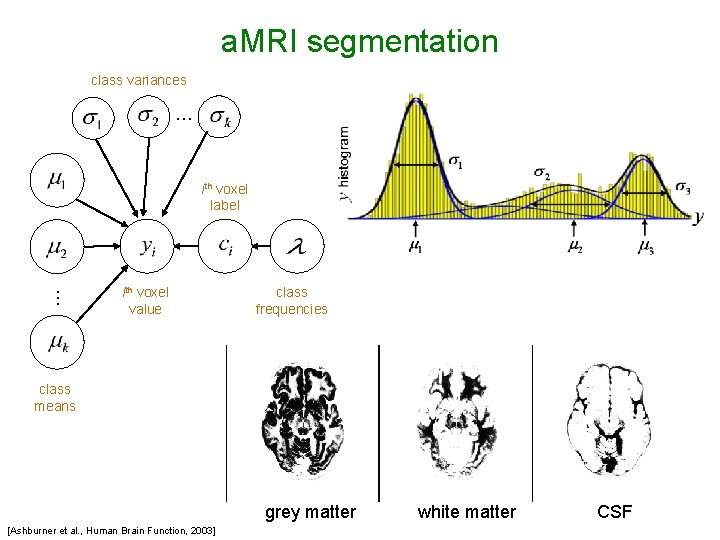
a. MRI segmentation class variances … … ith voxel label ith voxel value class frequencies class means grey matter [Ashburner et al. , Human Brain Function, 2003] white matter CSF

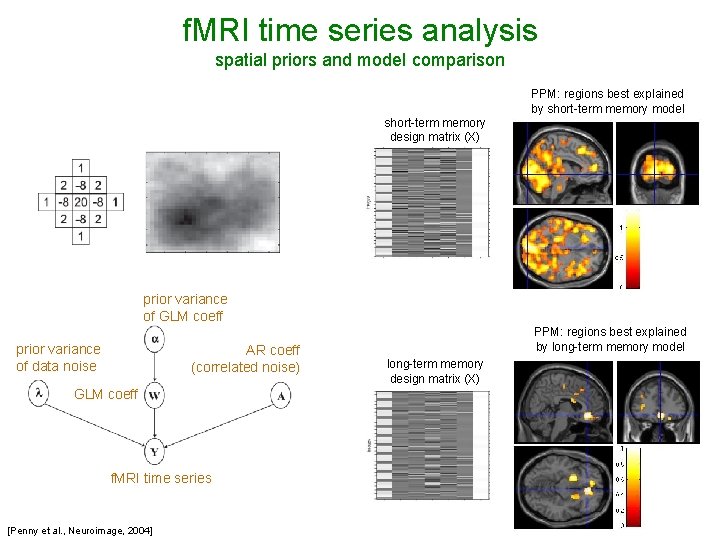
f. MRI time series analysis spatial priors and model comparison PPM: regions best explained by short-term memory model short-term memory design matrix (X) prior variance of GLM coeff prior variance of data noise AR coeff (correlated noise) GLM coeff f. MRI time series [Penny et al. , Neuroimage, 2004] PPM: regions best explained by long-term memory model long-term memory design matrix (X)

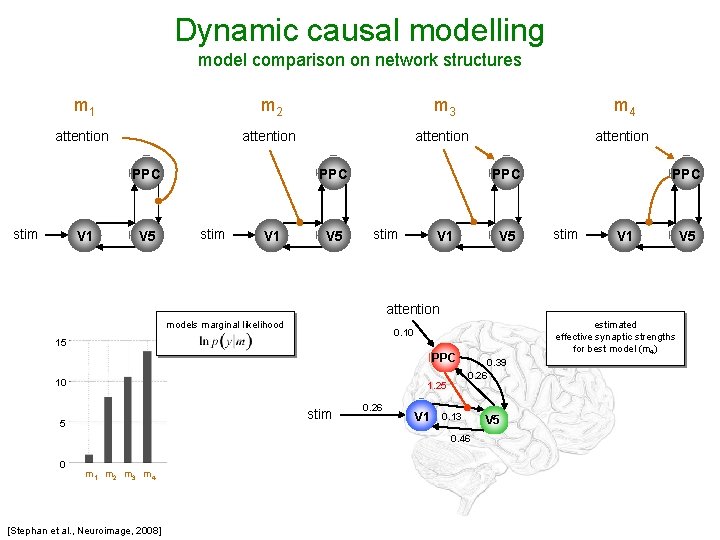
Dynamic causal modelling model comparison on network structures m 1 m 2 m 3 m 4 attention PPC stim V 1 V 5 PPC stim V 1 attention models marginal likelihood 15 PPC 10 1. 25 stim 5 estimated effective synaptic strengths for best model (m 4) 0. 10 0. 26 V 1 0. 39 0. 26 0. 13 0. 46 0 m 1 m 2 m 3 m 4 [Stephan et al. , Neuroimage, 2008] V 5

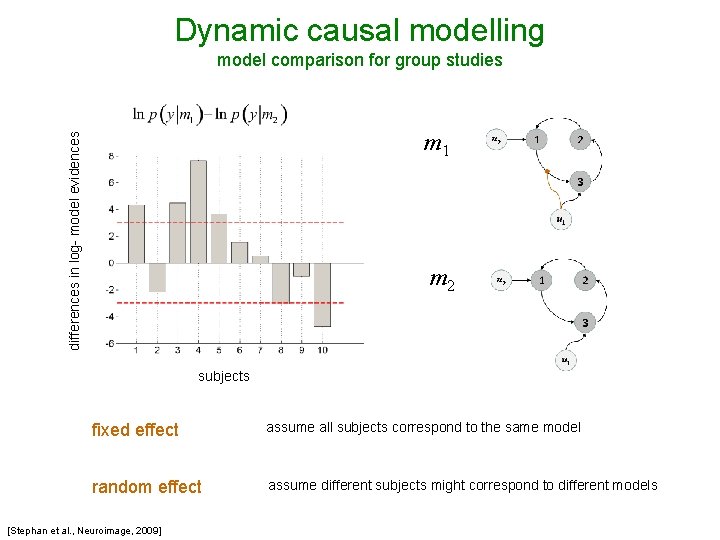
Dynamic causal modelling model comparison for group studies differences in log- model evidences m 1 m 2 subjects fixed effect assume all subjects correspond to the same model random effect assume different subjects might correspond to different models [Stephan et al. , Neuroimage, 2009]

EEG source reconstruction finessing an ill-posed inverse problem [Mattout et al. , Neuroimage, 2006]

Decoding of brain images recognizing brain states from f. MRI [Friston et al. , Neuroimage, 2008]

I thank you for your attention.

DCMs and DAGs a note on causality 1 1 1 2 2 3 time 1 2 3 3 u