Bayesian Hierarchical Model Ying Nian Wu UCLA Department

Bayesian Hierarchical Model Ying Nian Wu UCLA Department of Statistics IPAM Summer School July 12, 2007

Plan • Bayesian inference • Learning the prior • Examples • Josh’s example

Inference of normal mean independently unknown parameter given constant Example: one’s height repeated measurements known precision

Prior distribution known hyper-parameters The larger , the more uncertain about , prior becomes non-informative

Bayesian inference Prior: Data: independently Posterior: Compromise between prior and data

Bayesian inference Prior: Data: Posterior:

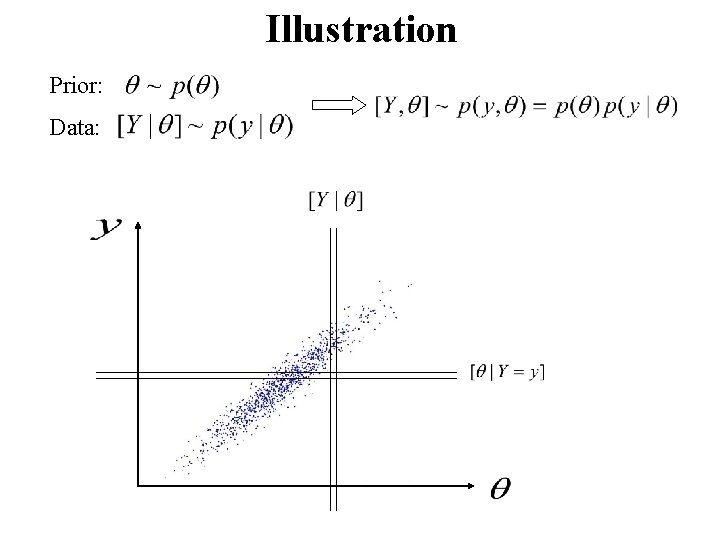
Illustration Prior: Data:

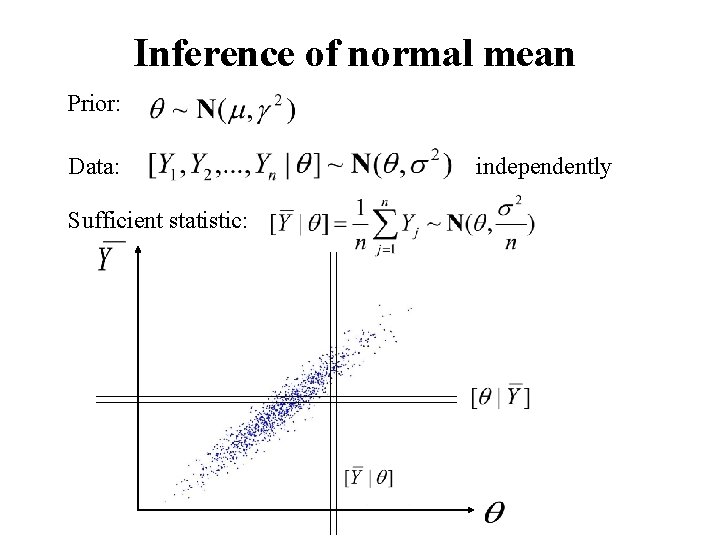
Inference of normal mean Prior: Data: Sufficient statistic: independently

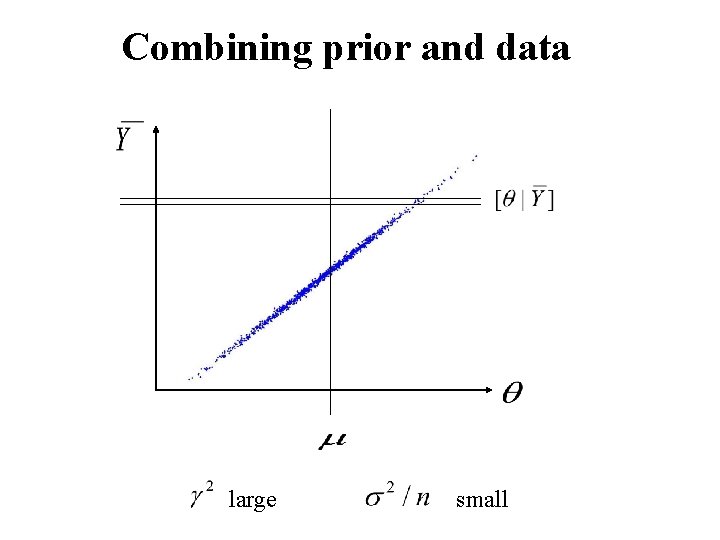
Combining prior and data large small

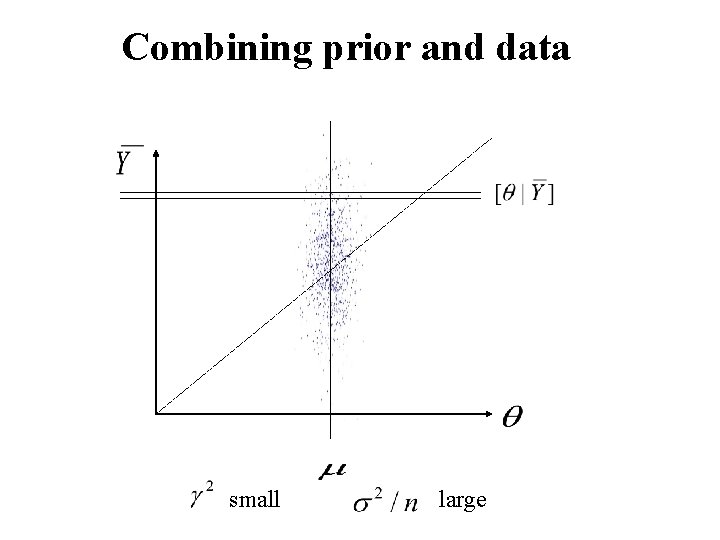
Combining prior and data small large

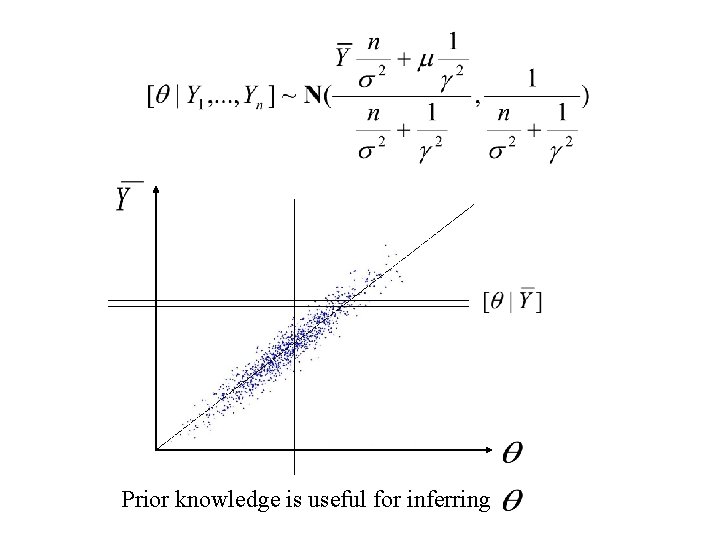
Prior knowledge is useful for inferring

Learning the prior Prior: Data: independently Prior distribution cannot be learned from single realization of

Learning the prior Prior: Data: Prior distribution can be learned from multiple experiences

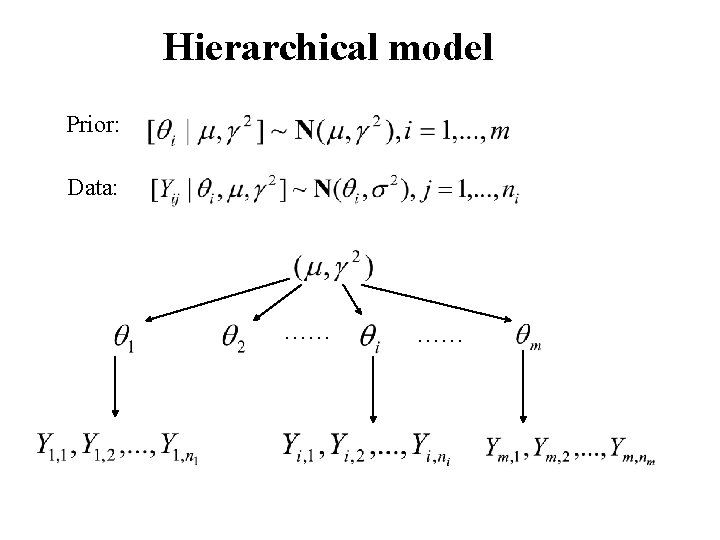
Hierarchical model Prior: Data: …… ……

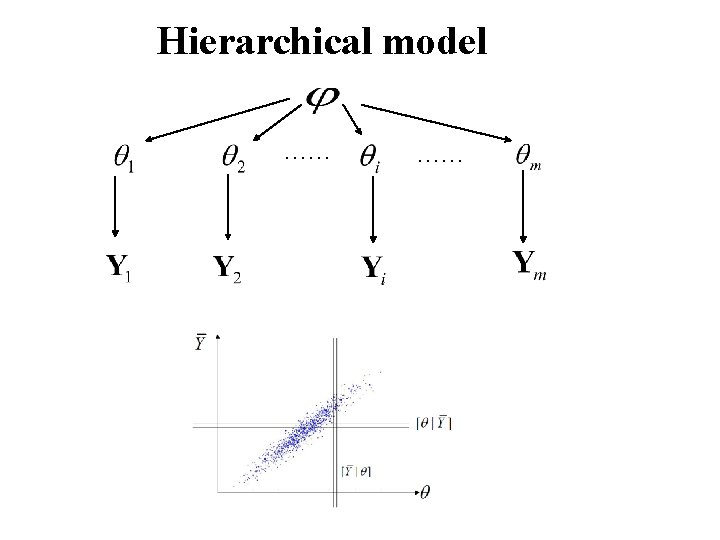
Hierarchical model …… ……

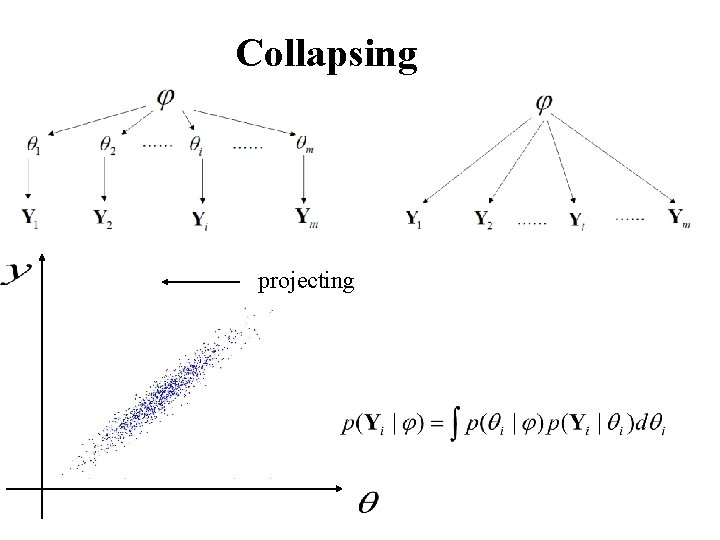
Collapsing projecting

Prior: Data: Sufficient statistics

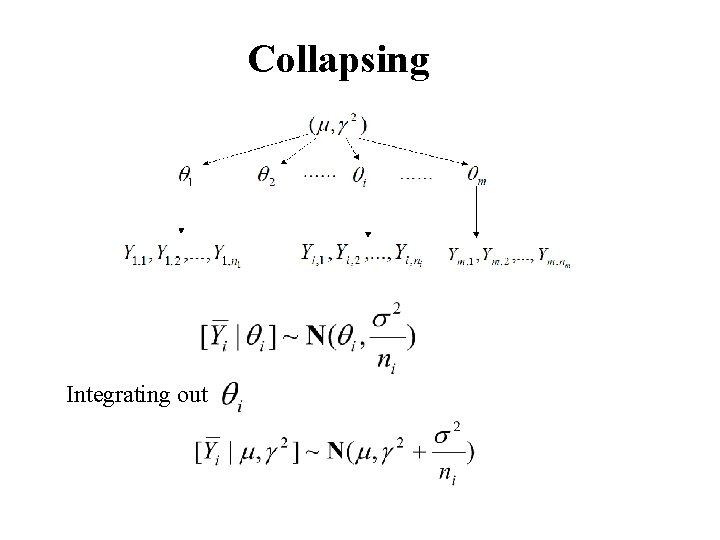
Collapsing Integrating out

Estimating hyper-parameter

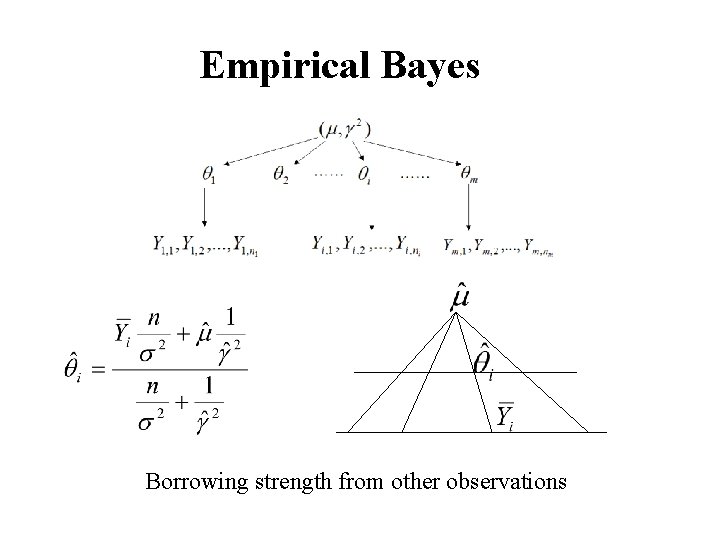
Empirical Bayes Borrowing strength from other observations

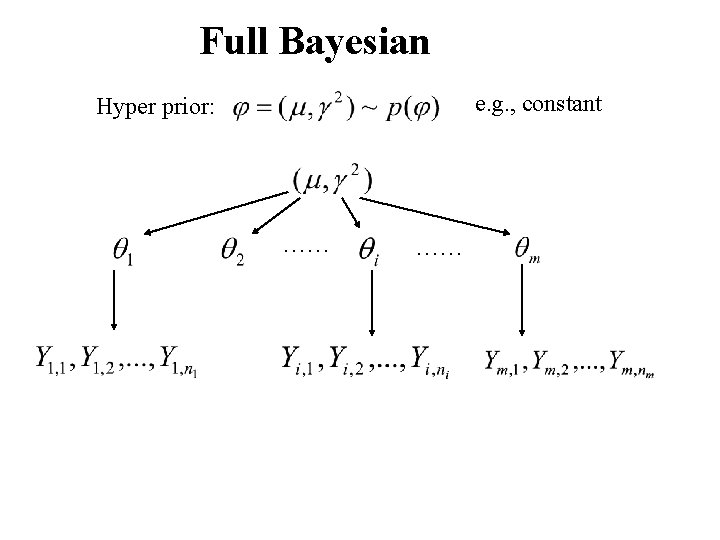
Full Bayesian e. g. , constant Hyper prior: …… ……

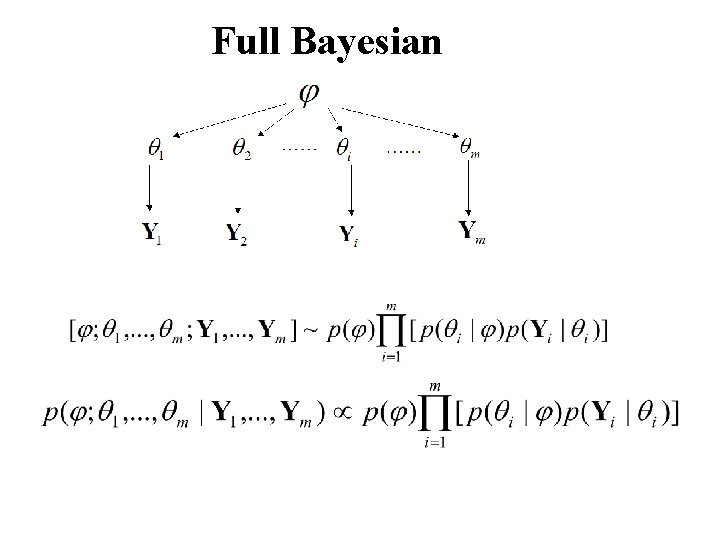
Full Bayesian

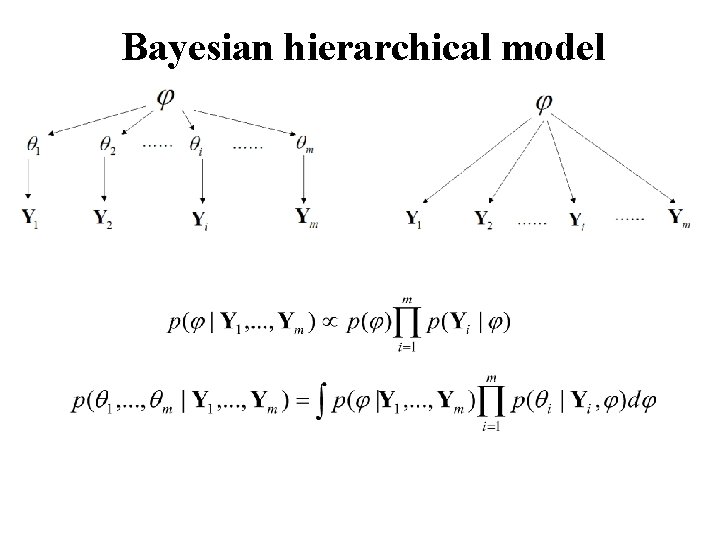
Bayesian hierarchical model

Stein’s estimator Example: measure each person’s height

Stein’s estimator

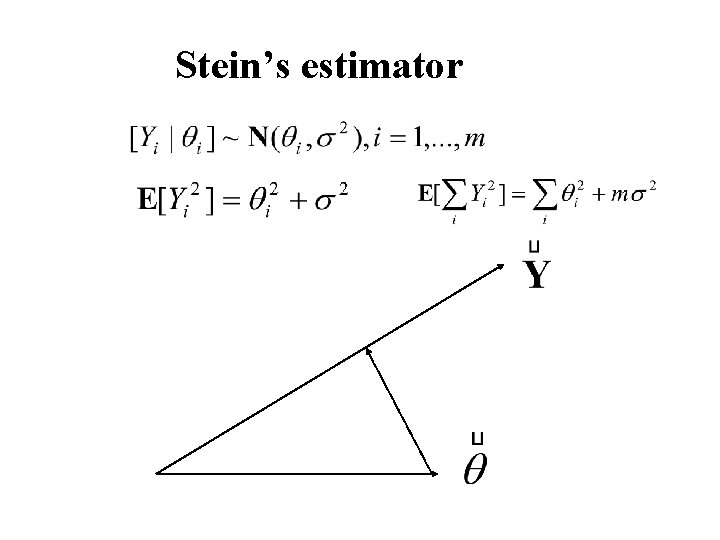
Stein’s estimator

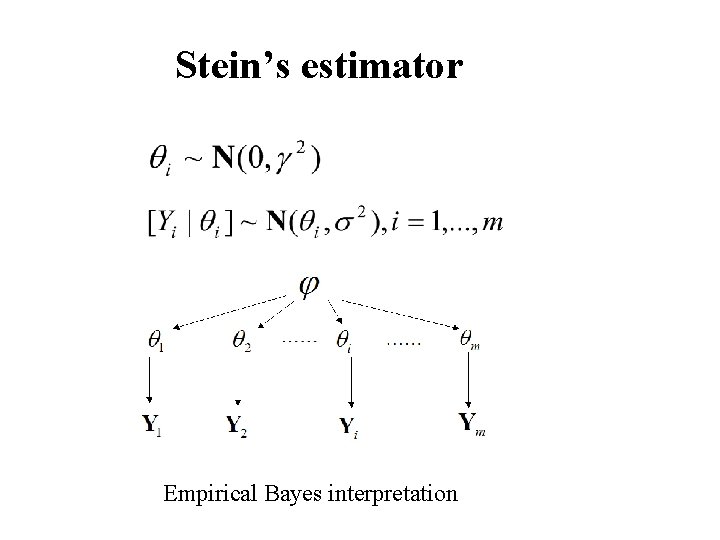
Stein’s estimator Empirical Bayes interpretation

Beta-Binomial example Data: e. g. , flip a coin, is probability of head is number of heads out of Pre-election poll flips

Conjugate prior

Data: Prior: Posterior:

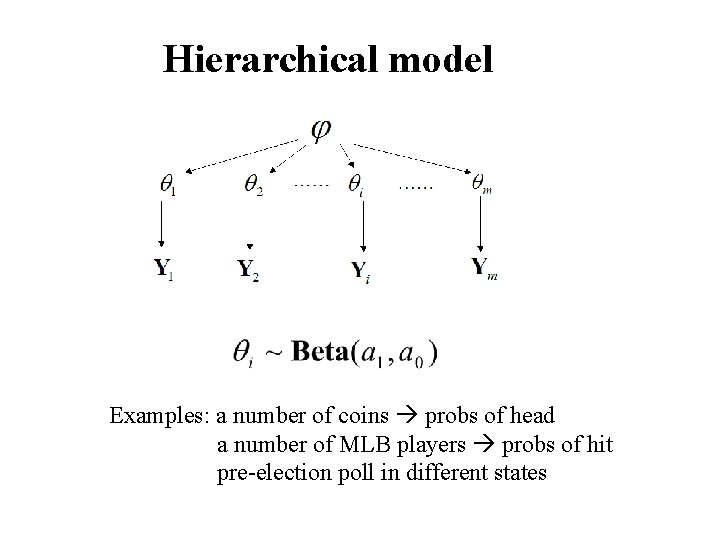
Hierarchical model Examples: a number of coins probs of head a number of MLB players probs of hit pre-election poll in different states

Dirichlet-Multinomial Roll a die:

Conjugate prior

Data Prior Posterior

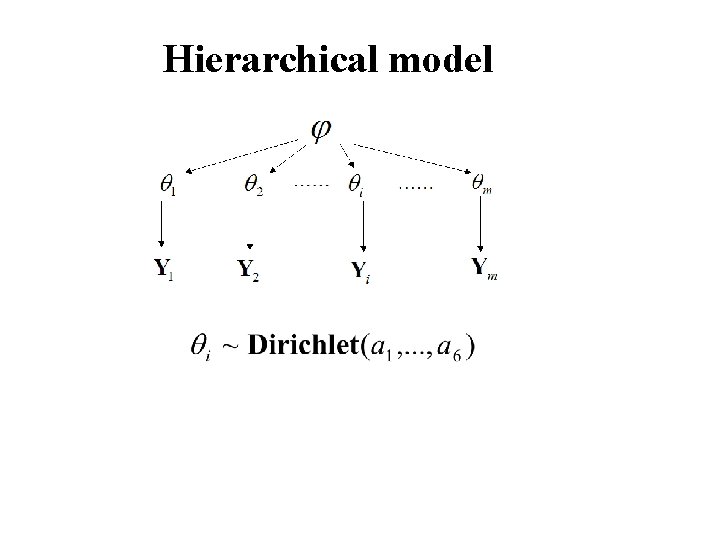
Hierarchical model