Bayesian Generalized Kernel Mixed Models Zhihua Zhang Guang

Bayesian Generalized Kernel Mixed Models Zhihua Zhang, Guang Dai and Michael I. Jordan JMLR 2011

Summary of contributions • Propose generalized kernel models (GKMs) as a framework in which sparsity can be given an explicit treatment and in which a fully Bayesian methodology can be carried out • Data augmentation methodology to develop a MCMC algorithm for inference • Approach shown to be related Gaussian processes and provide a flexible approximation method for GPs

Bayesian approach for kernel supervised learning • The form of the regressor or classifier is given by • For a Mercer kernel, there exists a corresponding mapping (say ), from the input space , such that • This provides an equivalent representation in the feature space, where,

Generalized Kernel Models

Prior for regression coefficients

Sparse models • Recall that the number of active vectors is the number of non-zero components of – We are thus interested in a prior for which allows some components of to be zero

Methodology For the indicator vector
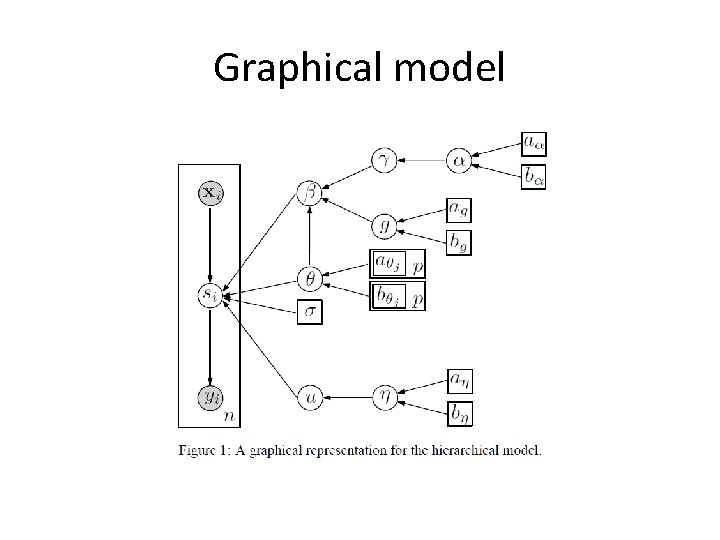
Graphical model

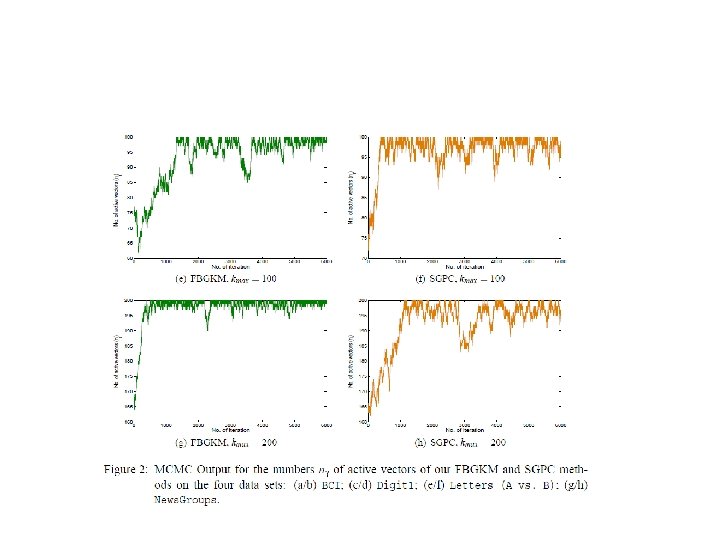
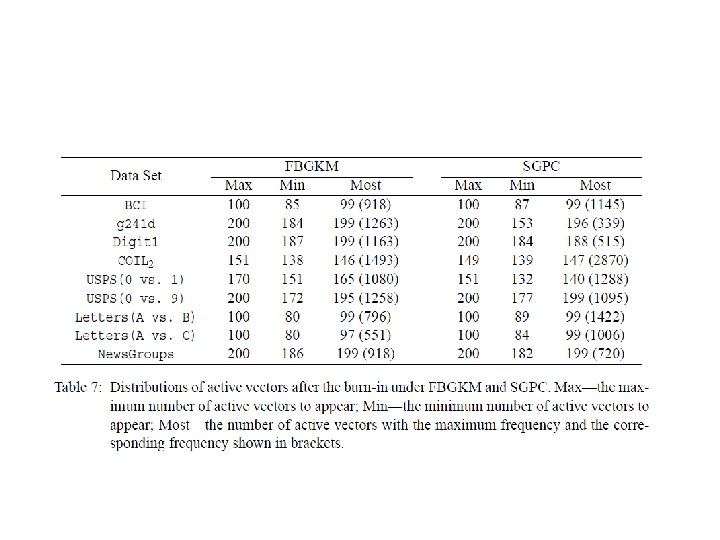
Inference • Gibbs for most parameters • MH for kernel parameters • Reversible jump Markov Chain for – takes 2^n distinct values – For small n, posterior may be obtained by calculating the normalizing constant by summing over all possible values of – For large n, a reversible jump MC sampler may be employed to identify high posterior probability models

Automatic choice of active vectors • We generate a proposal from the current value of by one of the three possible moves: Prediction :

Sparse Gaussian process for classification Given a function covariance function Also, , then is a Gaussian process with zero mean and vice versa.

Sparse GP classification
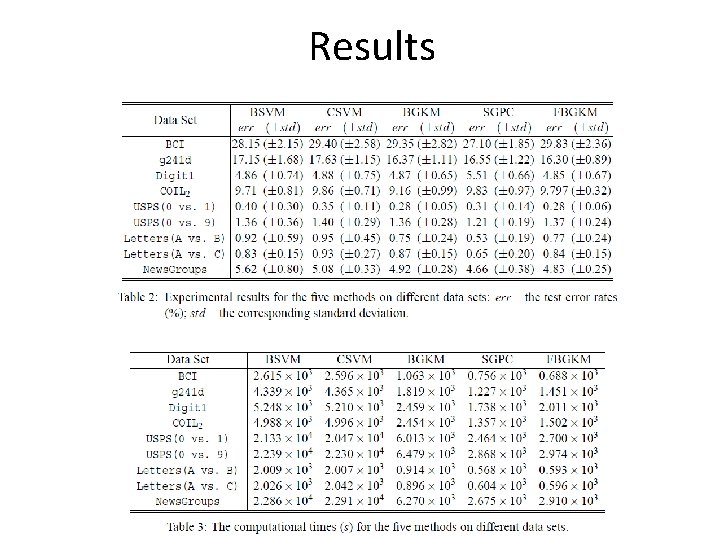
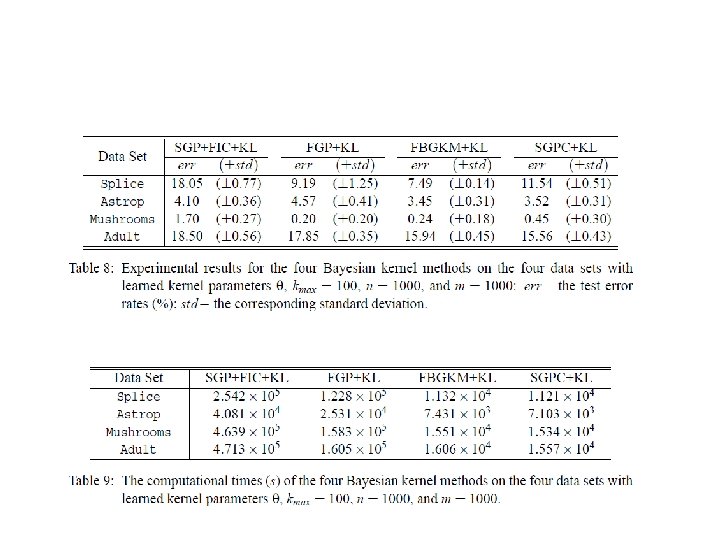
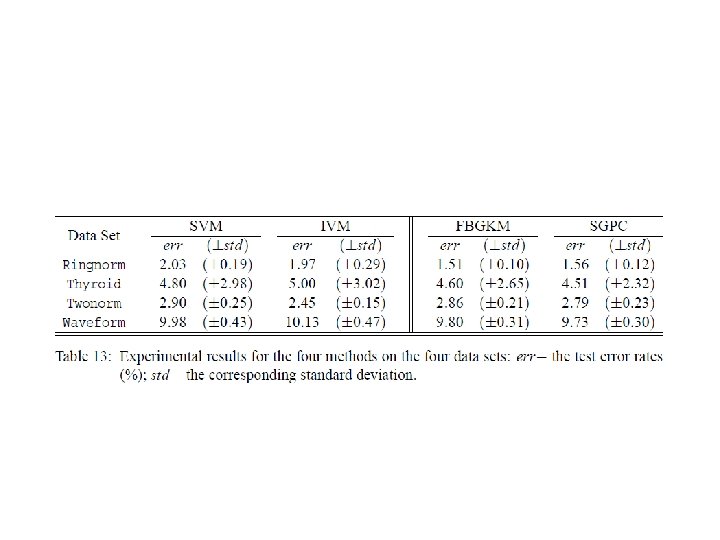
Results
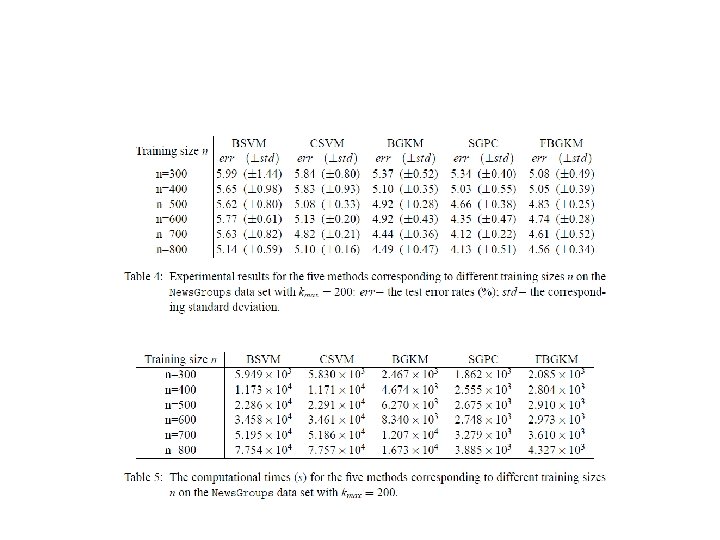
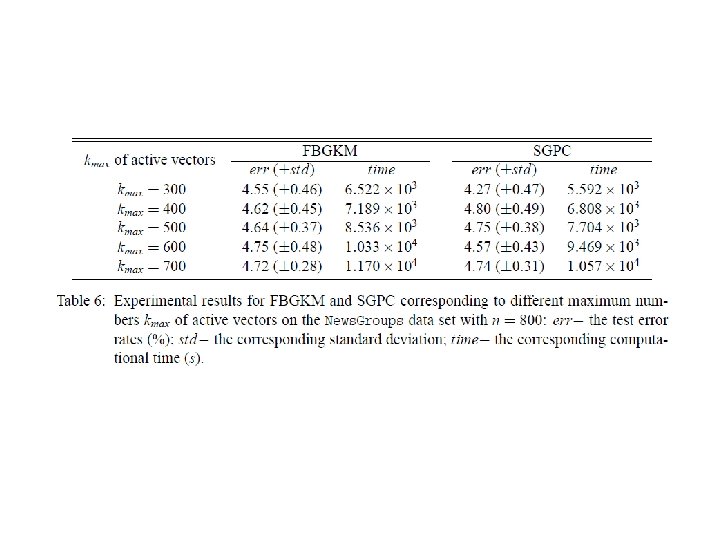
- Slides: 19