Bayesian AVO Inversion and Application to a Case

Bayesian AVO Inversion and Application to a Case Study Pål Dahle*, Ragnar Hauge, and Odd Kolbjørnsen Norwegian Computing Center Nam H. Pham Statoil
Contents Objective – Constrain high resolution 3 D reservoirs by seismic AVO data Method – Bayesian inversion, merging of geophysical and geological models Contribution – Fast algorithm – Spatial coupling – Uncertainty assessment Vp Vs
Outline Rapid spatially coupled AVO inversion Bayesian inversion 2) Earth model 3) Combining models 4) Summary Probability 1) Geophysical model Combined 5) Case study Geology Seismic Reservoir
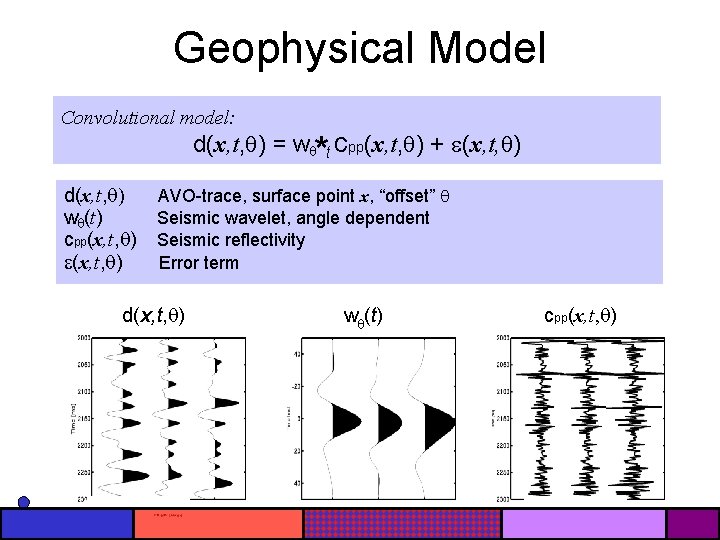
Geophysical Model Convolutional model: d(x, t, ) = w t cpp(x, t, ) + (x, t, ) d(x, t, ) w (t) cpp(x, t, ) * AVO-trace, surface point x, “offset” Seismic wavelet, angle dependent Seismic reflectivity Error term d(x, t, ) w (t) cpp(x, t, )

Reflectivity Convolutional model: d(x, t, ) = w t cpp(x, t, ) + (x, t, ) * Weak contrast approximation (continuous version): cpp(x, t, ) = a. Vp( ) ln. Vp(x, t) + a. Vs( ) ln. Vs(x, t) + a ( ) ln (x, t) t t t Matrix formulation: d = Gm + m(x, t) = [ ln. Vp(x, t), ln. Vs(x, t) , ln (x, t) ]

Assuming Normal Distributions m ~ N( m, m) ~ N(0, e) d ~ N( md, d) Matrix formulation: d = Gm + m(x, t) = [ ln. Vp(x, t), ln. Vs(x, t) , ln (x, t) ]
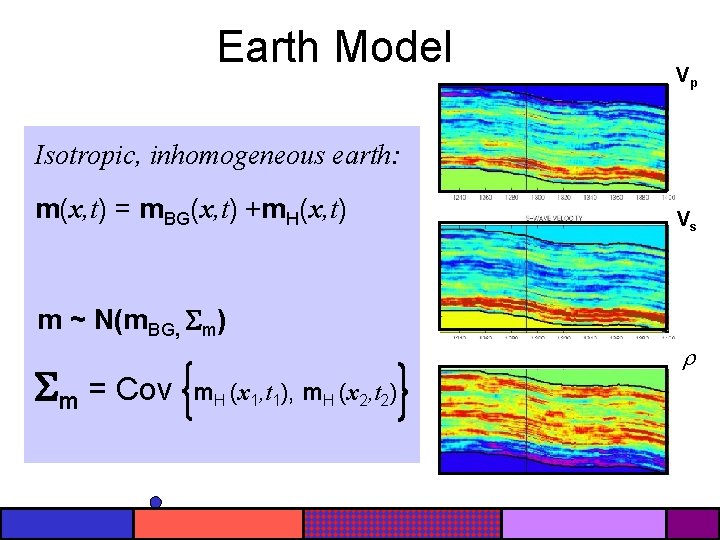
Earth Model Vp Isotropic, inhomogeneous earth: m(x, t) = m. BG(x, t) +m. H(x, t) m ~ N(m. BG, m) m = Cov m. H (x 1, t 1), m. H (x 2, t 2) Vs
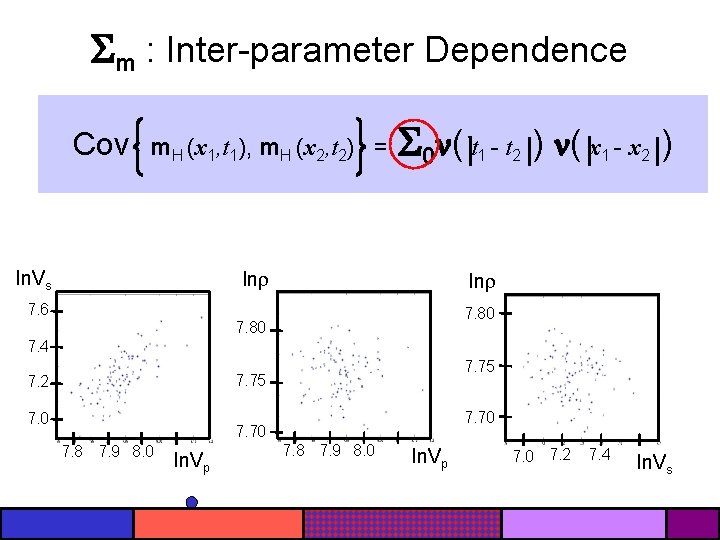
m : Inter-parameter Dependence Cov m. H (x 1, t 1), m. H (x 2, t 2) = ln. Vs 0 ( t ln 1 - t 2 ) ( x 1 - x 2 ) ln 7. 6 7. 80 7. 4 7. 75 7. 2 7. 0 7. 70 7. 8 7. 9 8. 0 ln. Vp 7. 0 7. 2 7. 4 ln. Vs
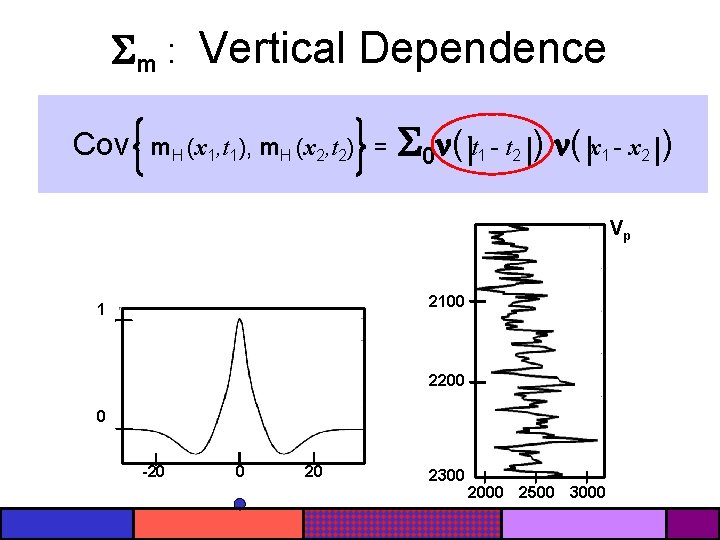
m : Vertical Dependence Cov m. H (x 1, t 1), m. H (x 2, t 2) = 0 ( t 1 - t 2 ) ( x 1 - x 2 ) Vp 2100 1 2200 0 -20 0 20 2300 2000 2500 3000
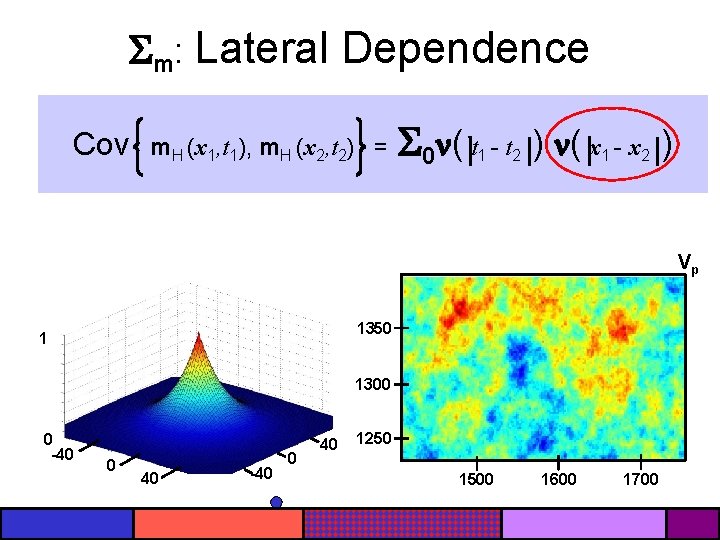
m: Lateral Dependence Cov m. H (x 1, t 1), m. H (x 2, t 2) = 0 ( t 1 - t 2 ) ( x 1 - x 2 ) Vp 1350 1 1300 0 -40 0 40 1250 1500 1600 1700

Combining the Models m ~ N( m, m) ~ N(0, e) d ~ N( md, d) m d ~ N( mm|d , m|d)
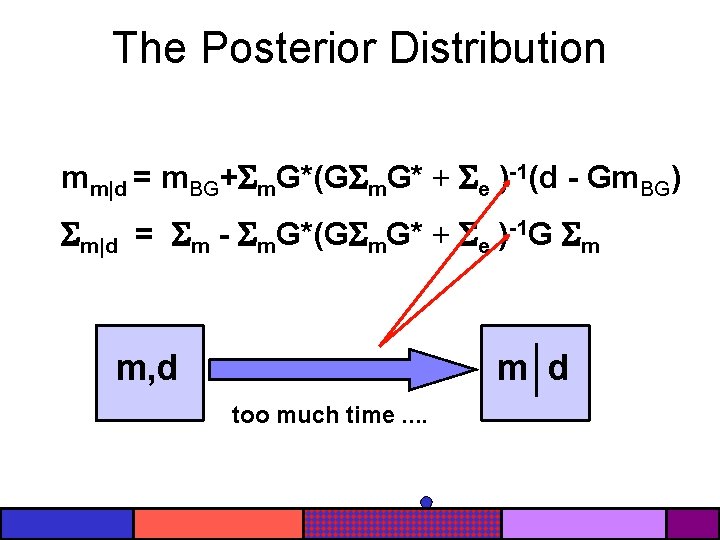
The Posterior Distribution mm|d = m. BG+ m. G*(G m. G* + e )-1(d - Gm. BG) m|d = m - m. G*(G m. G* + e )-1 G m m, d m d too much time. .
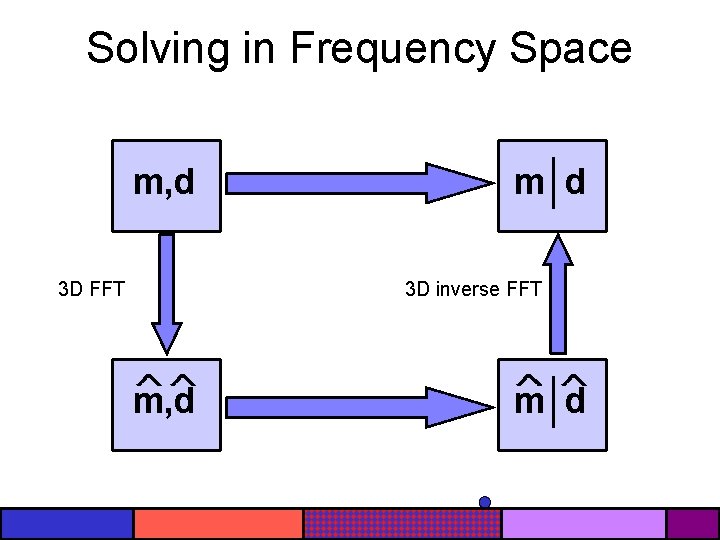
Solving in Frequency Space m, d 3 D FFT m d 3 D inverse FFT m, d m d
Summary • Bayesian inversion • Convolutional model, weak contrast • Spatial dependencies of earth parameters • Fast inversion • 100 million grid cells ~ 1 hour • More than inversion • Consistent merging of well logs • High resolution reservoirs
Smørbukk Case Study
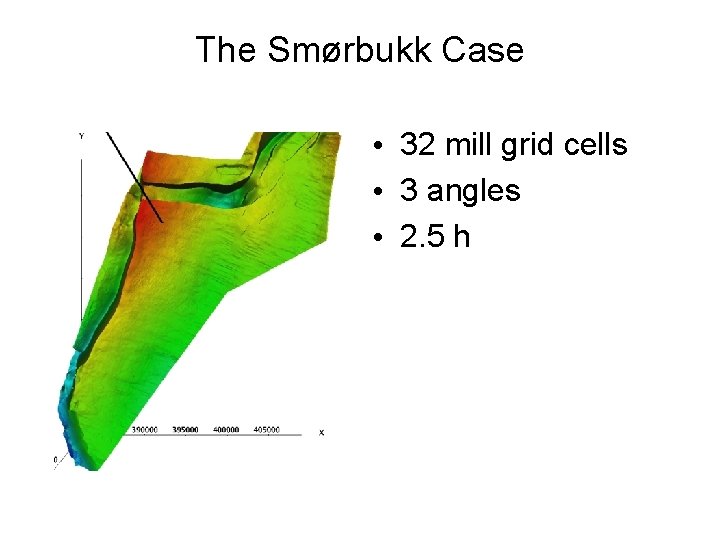
The Smørbukk Case • 32 mill grid cells • 3 angles • 2. 5 h
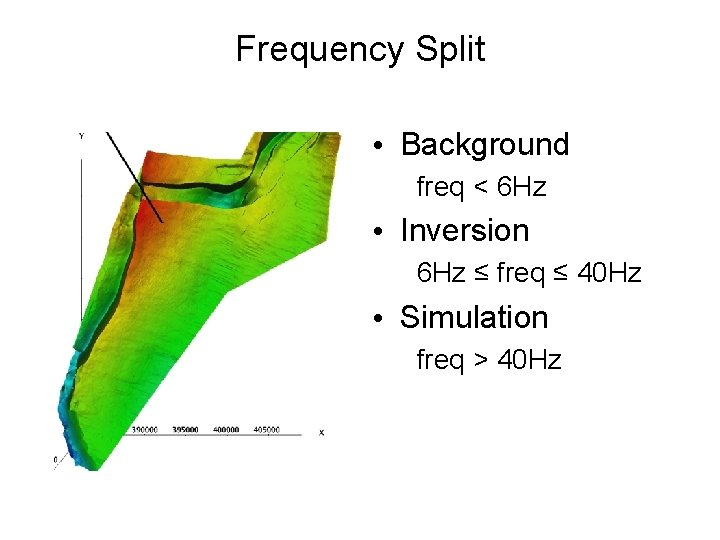
Frequency Split • Background freq < 6 Hz • Inversion 6 Hz ≤ freq ≤ 40 Hz • Simulation freq > 40 Hz
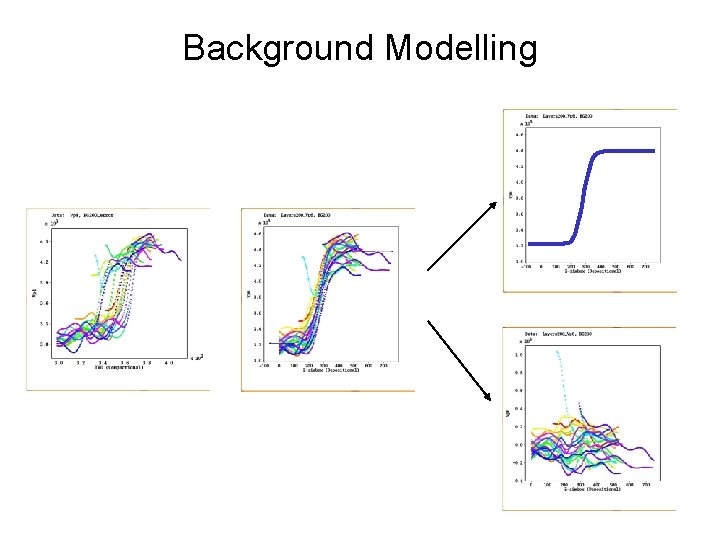
Background Modelling
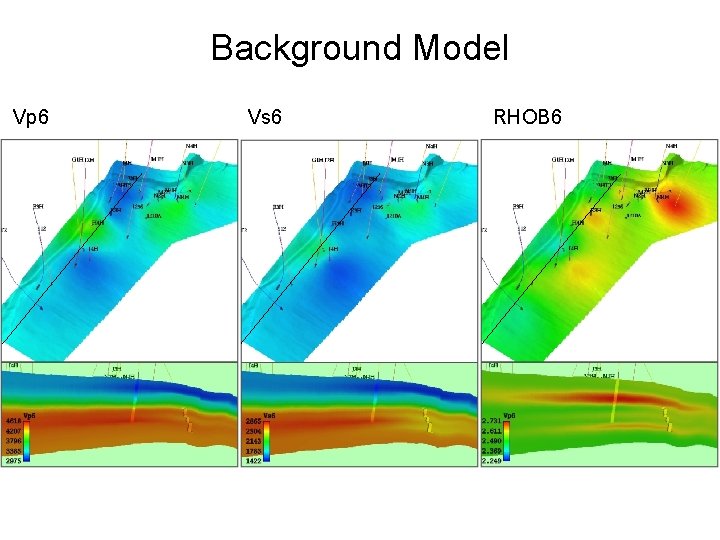
Background Model Vp 6 Vs 6 RHOB 6

Inversion Input Data • Background model: Vp, Vs, and Rho • Well data: TWT, DTS, and Rho • Seismic Data • Wavelets
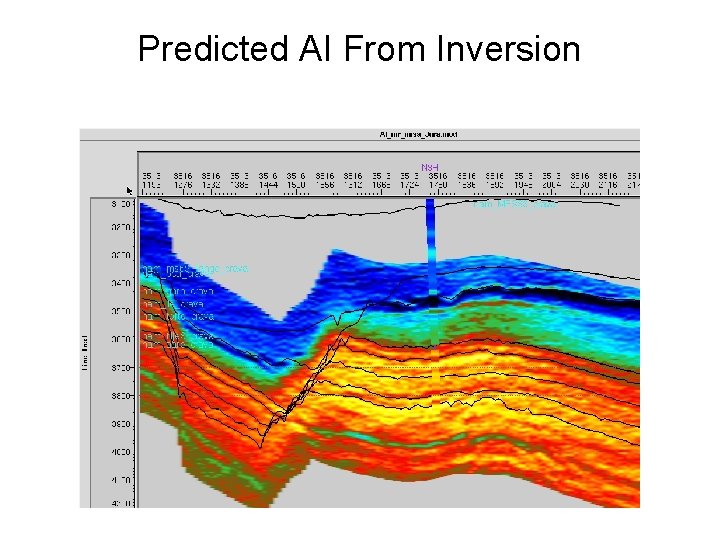
Predicted AI From Inversion
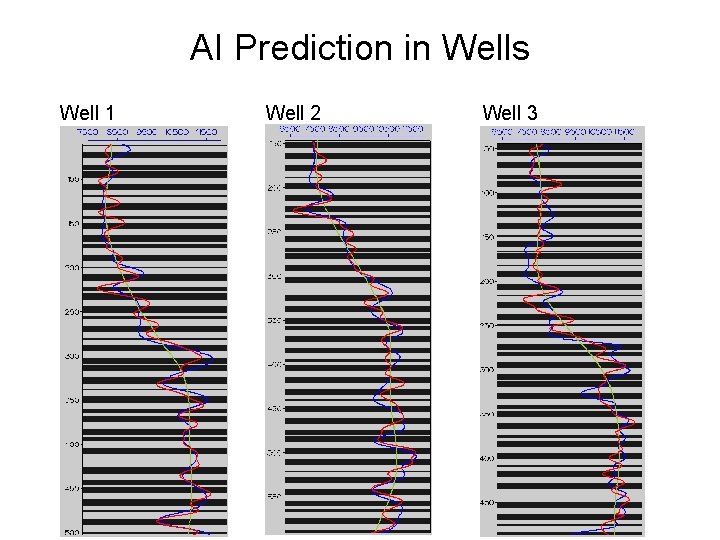
AI Prediction in Wells Well 1 Well 2 Well 3
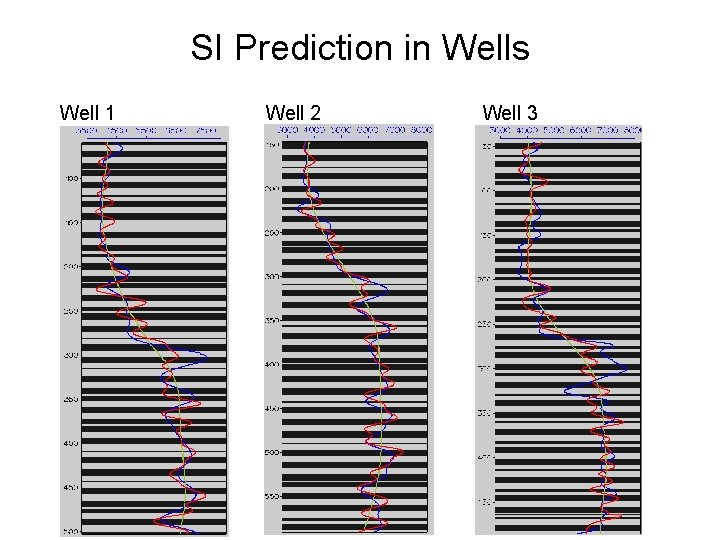
SI Prediction in Wells Well 1 Well 2 Well 3
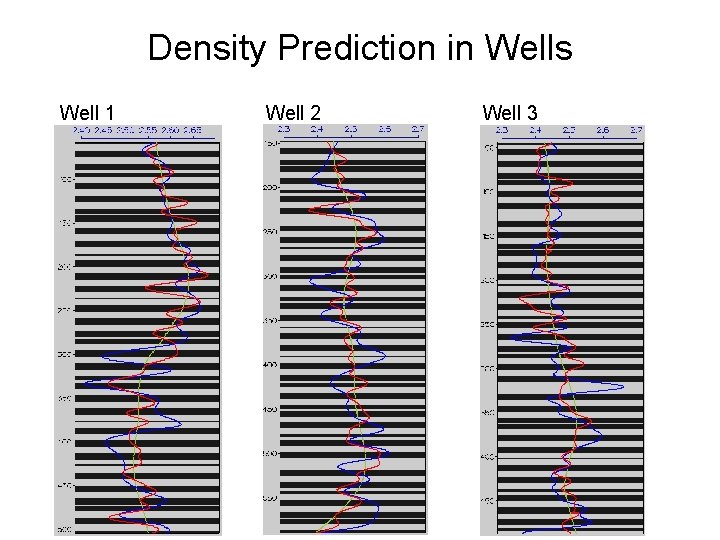
Density Prediction in Wells Well 1 Well 2 Well 3

AI Cross Sections: Horisontal
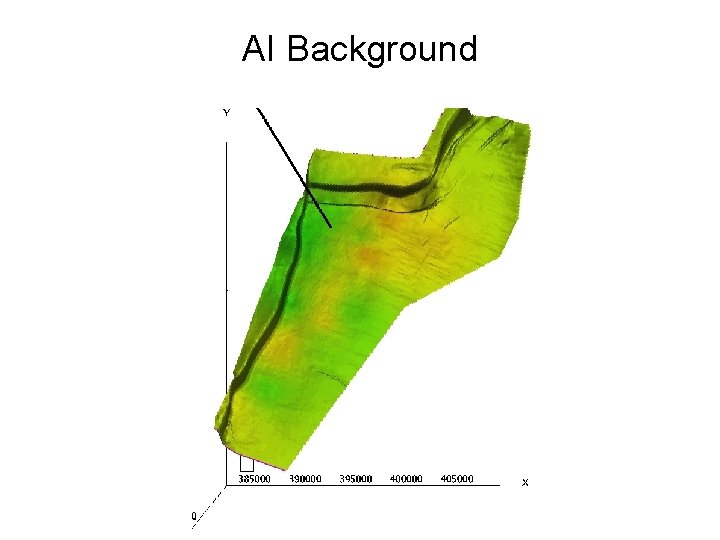
AI Background
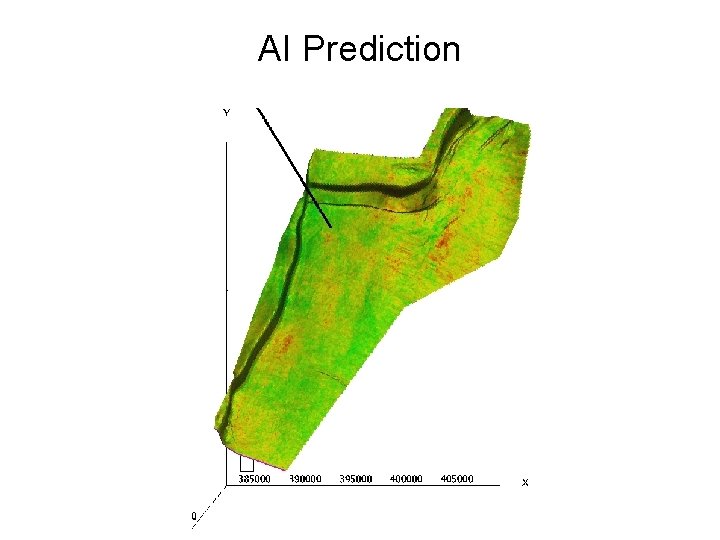
AI Prediction
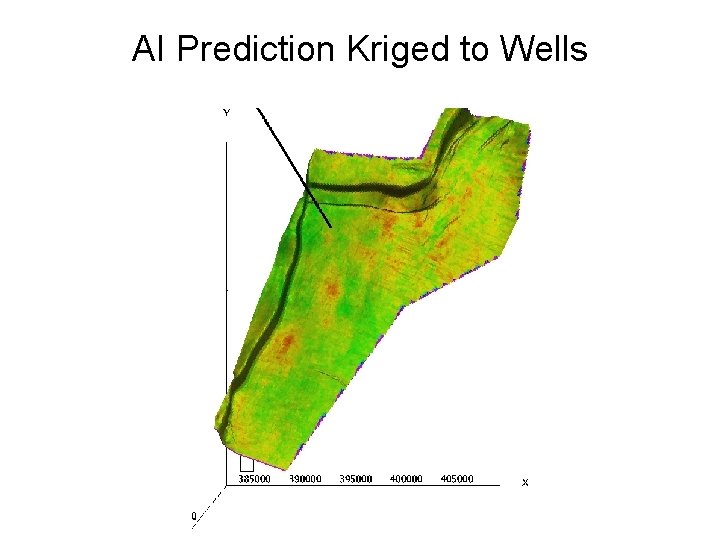
AI Prediction Kriged to Wells
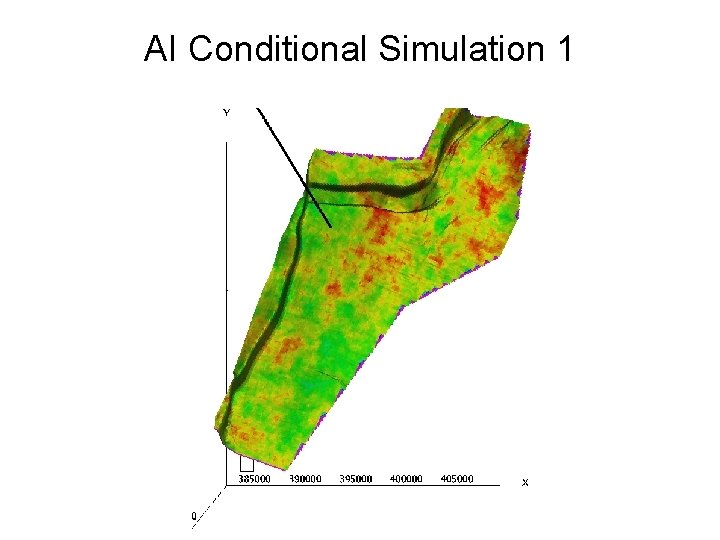
AI Conditional Simulation 1
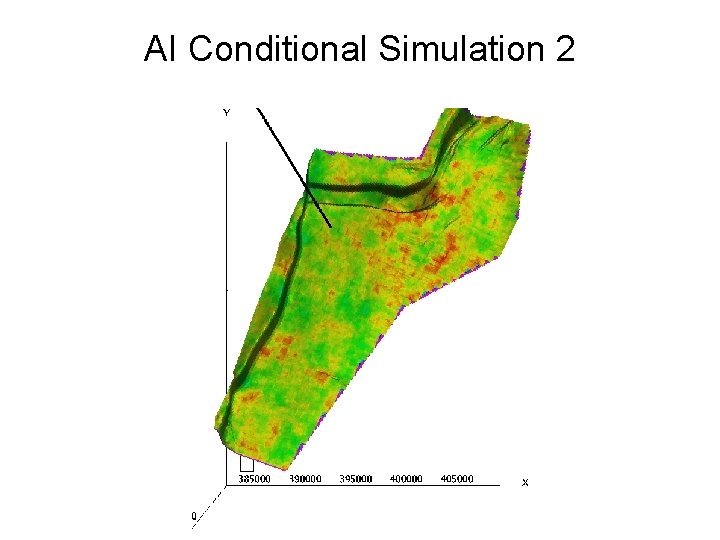
AI Conditional Simulation 2

AI Cross Sections: Vertical
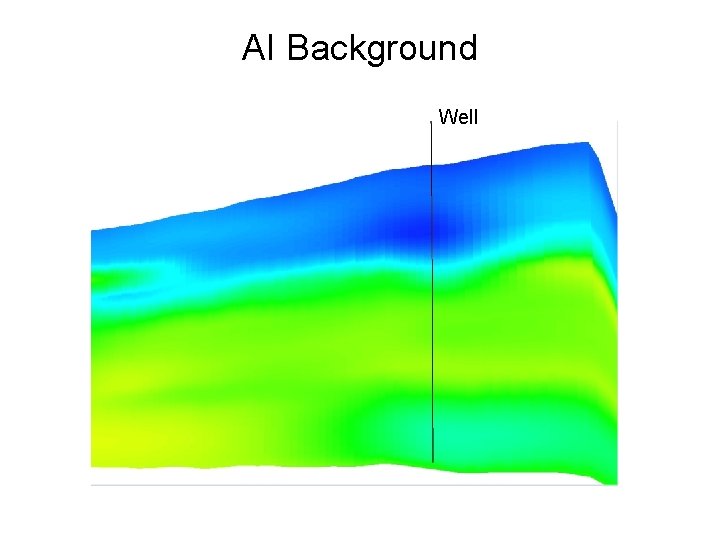
AI Background Well
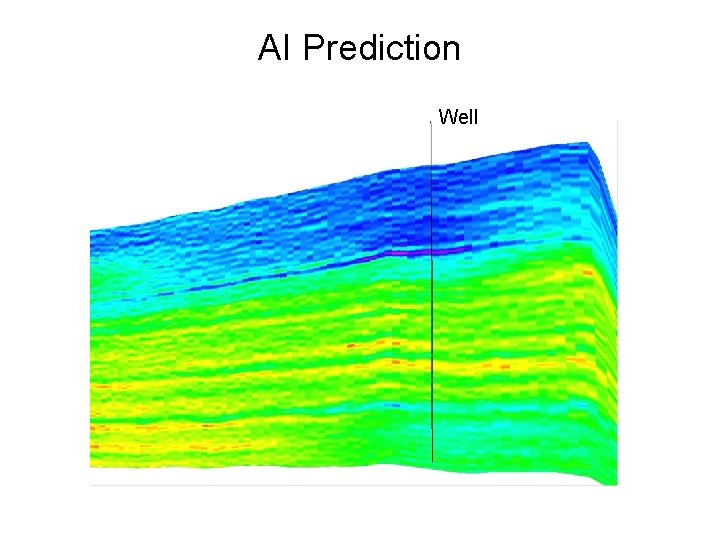
AI Prediction Well
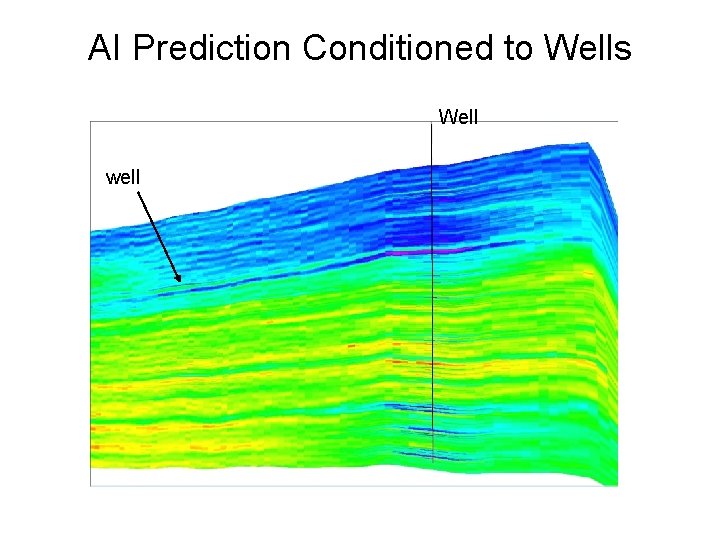
AI Prediction Conditioned to Wells Well well
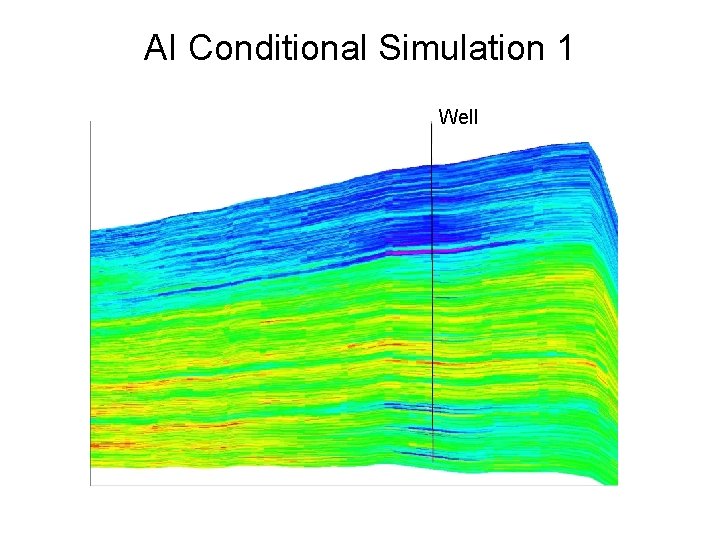
AI Conditional Simulation 1 Well
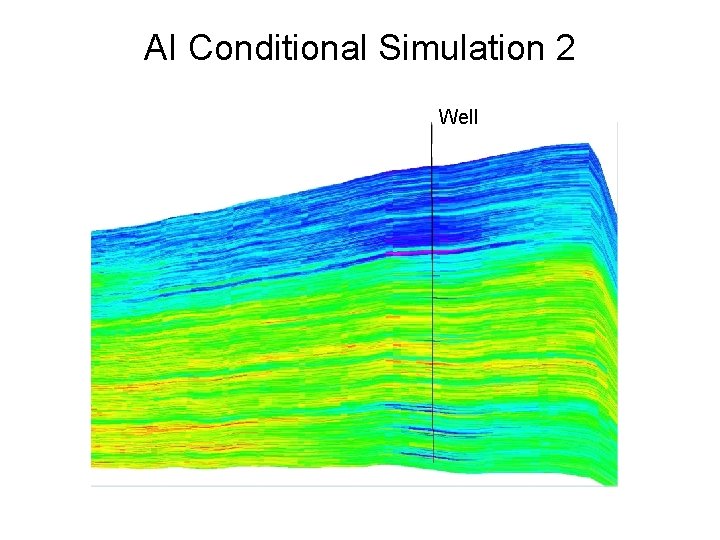
AI Conditional Simulation 2 Well

Case Study Conclusions • Good match for AI used for modelling of – Facies – Porosity
- Slides: 37