Bayesian analysis of extremes in hydrology A powerful

Bayesian analysis of extremes in hydrology A powerful tool for knowledge integration and uncertainties assessment Renard, B. , Garreta, V. , Lang, M. and Bois, P.

Introduction Water is both a resource and a risk High flows risk… …and low flows risk → Hydrologists are interested in the tail of the discharges distribution Extreme Value Analysis, August 15 -19, 2005

Introduction General analysis scheme ü Extract a sample of extreme values from the discharges series ü Choose a convenient extreme value distribution ü Estimate parameters ü Compute quantities of interest (quantiles) Estimation methods: moments, L-moments, maximum likelihood, Bayesian estimation Extreme Value Analysis, August 15 -19, 2005

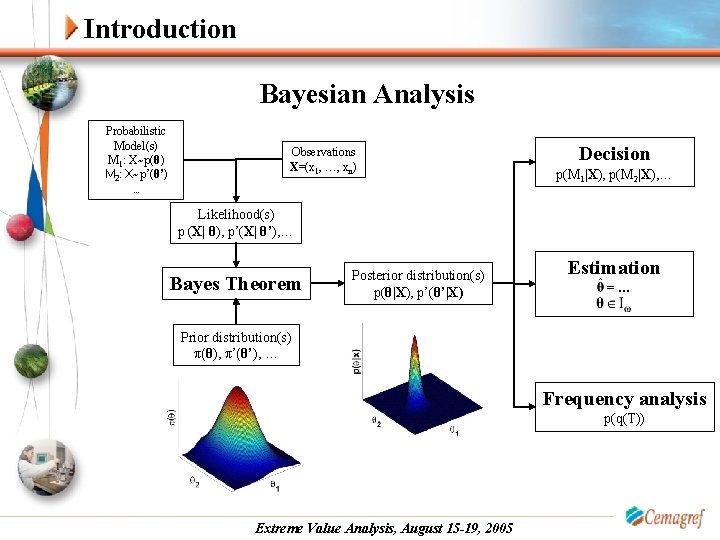
Introduction Bayesian Analysis Probabilistic Model(s) M 1: X~p(θ) M 2: X~p’(θ’) … Observations X=(x 1, …, xn) Decision p(M 1|X), p(M 2|X), … Likelihood(s) p (X| θ), p’(X| θ’), … Bayes Theorem Posterior distribution(s) p(θ|X), p’(θ’|X) Estimation =… Prior distribution(s) π(θ), π’(θ’), … Frequency analysis p(q(T)) Extreme Value Analysis, August 15 -19, 2005

Introduction Advantages from an hydrological point of view: Prior knowledge introduction: taking advantage of the physical processes creating the flow (rainfall, watershed topography, …) Model choice: computation of models probabilities, and incorporation of model uncertainties by « model averaging » Drawback for new user: MCMC algorithms… We used combinations of Gibbs and Metropolis samplers, with adaptive jumping rules as suggested by Gelman et al. (1995) Extreme Value Analysis, August 15 -19, 2005

The Ardeche river at St Martin d’Ardeche 2240 km 2 High slopes and granitic rocks on the top of the catchment Very intense precipitations (September-December) Extreme Value Analysis, August 15 -19, 2005

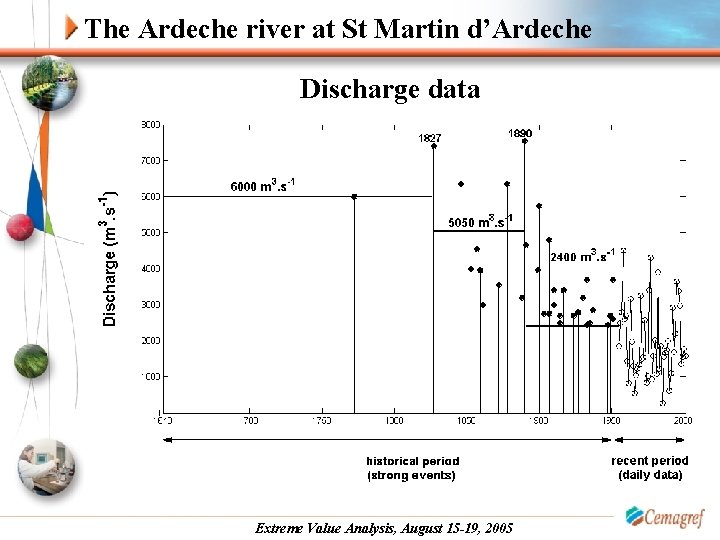
The Ardeche river at St Martin d’Ardeche Discharge data Extreme Value Analysis, August 15 -19, 2005

The Ardeche river at St Martin d’Ardeche Model: Annual Maxima follow a GEV distribution Likelihood: Extreme Value Analysis, August 15 -19, 2005

The Ardeche river at St Martin d’Ardeche Prior specifications Hydrological methods give rough estimates of quantiles: CRUPEDIX method: use watershed surface, daily rainfall quantile and geographical localization (q 10) Gradex method: use extreme rainfall distribution and expert’s judgment about response time of the watershed (q 200 -q 10) Record floods analysis: use discharges data on an extended geographical scale (q 1000) The prior distribution on quantiles is then transformed in a prior distribution on parameters Extreme Value Analysis, August 15 -19, 2005

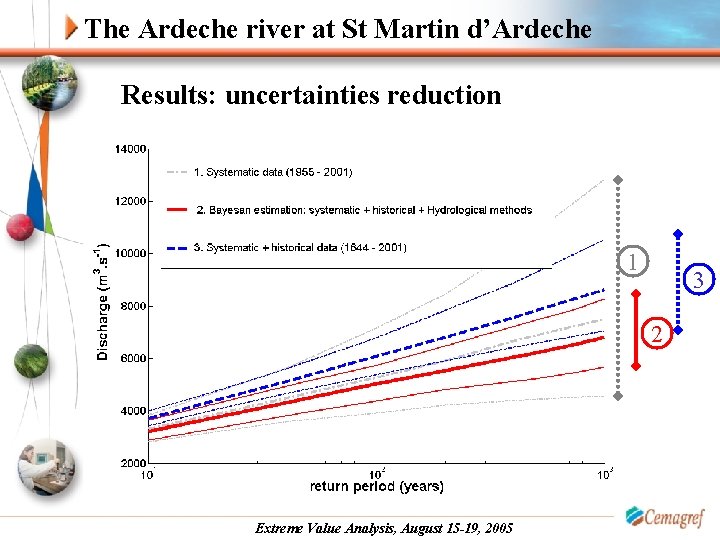
The Ardeche river at St Martin d’Ardeche Results: uncertainties reduction 1 3 2 Extreme Value Analysis, August 15 -19, 2005

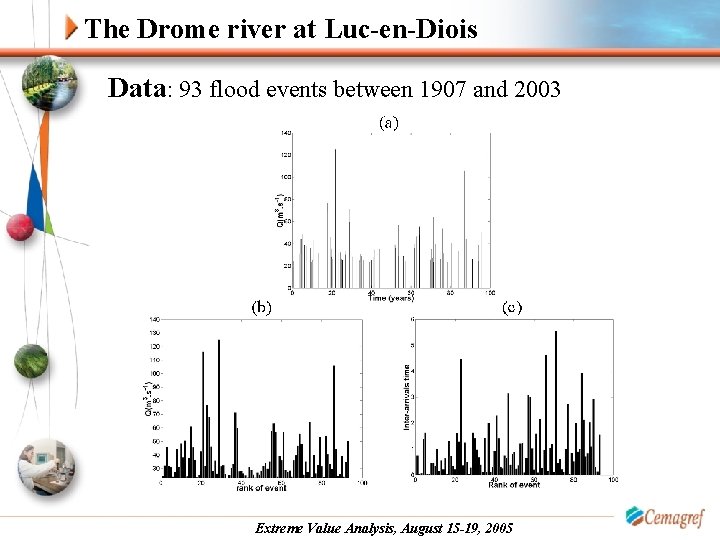
The Drome river at Luc-en-Diois Data: 93 flood events between 1907 and 2003 Extreme Value Analysis, August 15 -19, 2005

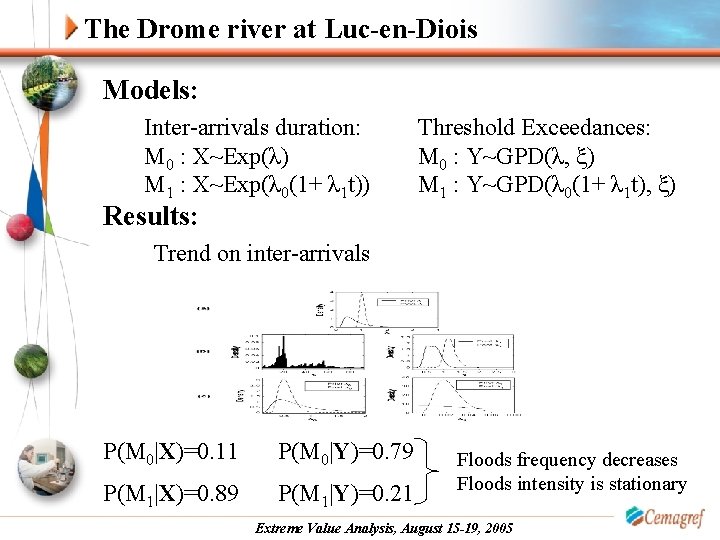
The Drome river at Luc-en-Diois Models: Inter-arrivals duration: M 0 : X~Exp(λ) M 1 : X~Exp(λ 0(1+ λ 1 t)) Results: Threshold Exceedances: M 0 : Y~GPD(λ, ξ) M 1 : Y~GPD(λ 0(1+ λ 1 t), ξ) Trend on inter-arrivals P(M 0|X)=0. 11 P(M 0|Y)=0. 79 P(M 1|X)=0. 89 P(M 1|Y)=0. 21 Floods frequency decreases Floods intensity is stationary Extreme Value Analysis, August 15 -19, 2005

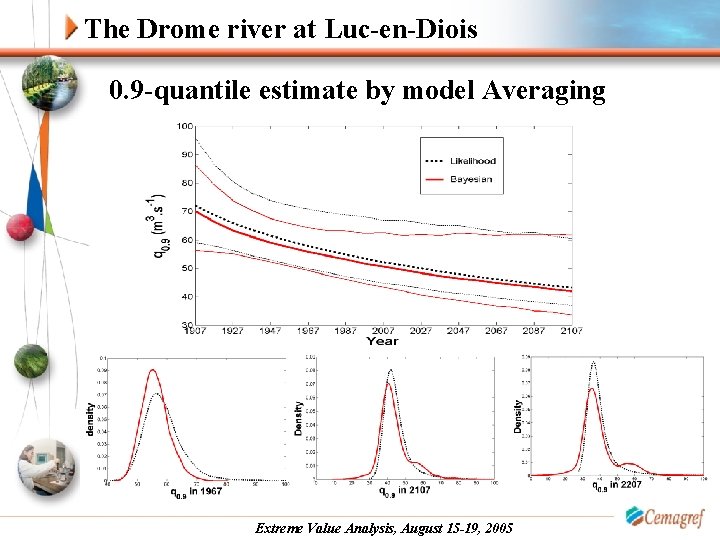
The Drome river at Luc-en-Diois 0. 9 -quantile estimate by model Averaging Extreme Value Analysis, August 15 -19, 2005

Perspectives: regional trend detection Motivations Regional model can improve estimators accuracy Climate change impacts should be regionally consistent Models Let denotes the annual maxima at site i at time t Extreme Value Analysis, August 15 -19, 2005

Perspectives: regional trend detection Likelihoods The multivariate distribution of annual maxima is needed… Independence hypothesis: Gaussian copula approximation: cumulated probability Gaussian Transformation Multivariate Gaussian model Extreme Value Analysis, August 15 -19, 2005

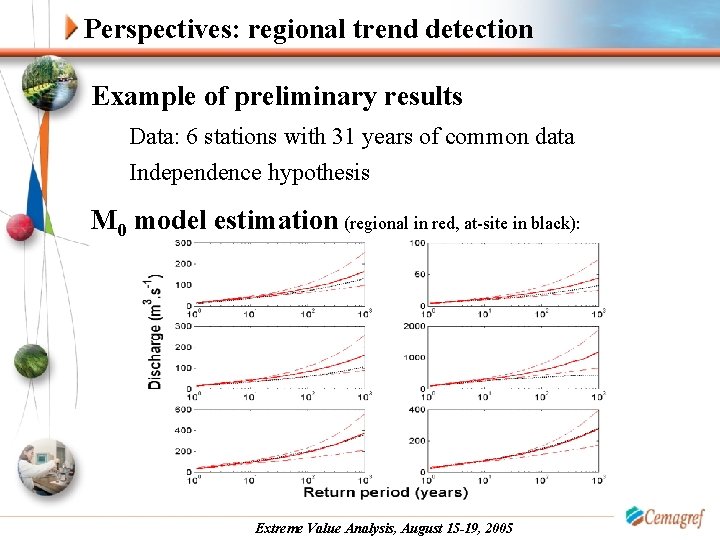
Perspectives: regional trend detection Example of preliminary results Data: 6 stations with 31 years of common data Independence hypothesis M 0 model estimation (regional in red, at-site in black): Extreme Value Analysis, August 15 -19, 2005

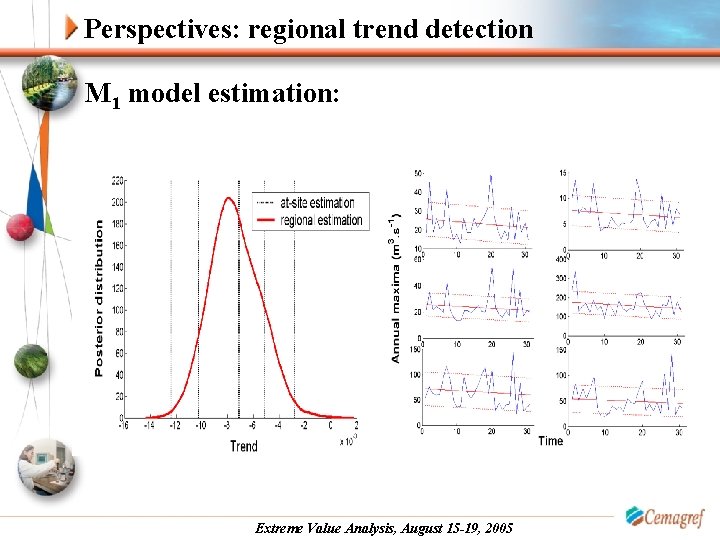
Perspectives: regional trend detection M 1 model estimation: Extreme Value Analysis, August 15 -19, 2005

Conclusion Advantages of Bayesian analysis ü Prior knowledge integration ü Model choice uncertainty is taken into account ü No asymptotic assumption ü Robustness of MCMC methods to deal with high dimensional problems But… ü Part of subjectivity? ü A better understanding of extreme’s dependence is still needed Extreme Value Analysis, August 15 -19, 2005