Bayesian Adaptive Designs for Dose Escalation Studies Midwest

Bayesian Adaptive Designs for Dose Escalation Studies Midwest Biopharmaceutical Statistics Workshop Anna Mc. Glothlin 20 May 2009

Contents Traditional Dose Escalation Design (and its shortcomings) The Continual Reassessment Method An example trial using CRM Simulation and Operating Characteristics Overview of other novel designs Summary 6/3/2021 Anna Mc. Glothlin 2

Motivation Why should you care about novel designs for dose escalation studies? Traditional designs are not reliable for selecting the correct maximum tolerated dose Wrong dose carried forward to future trials. Standard design tends to treat a high percentage of patients at doses outside of therapeutic range. Novel designs are better for patients! 6/3/2021 Anna Mc. Glothlin 3

Dose Escalation Studies Typically small, uncontrolled* studies. GOAL: Determine the maximum tolerated dose (MTD), and/or a recommended Phase II dose. Two Approaches: 1. Algorithm-based designs – – 2. 3+3 (or the more general A+B) MTD is identified as the dose with fewer than some proportion of dose limiting toxicities (e. g. <1/3). Model-based designs – MTD is estimated as a quantile of the dose-toxicity curve * Design may be modified to allow for a control. This will be briefly discussed later. 6/3/2021 Anna Mc. Glothlin 4

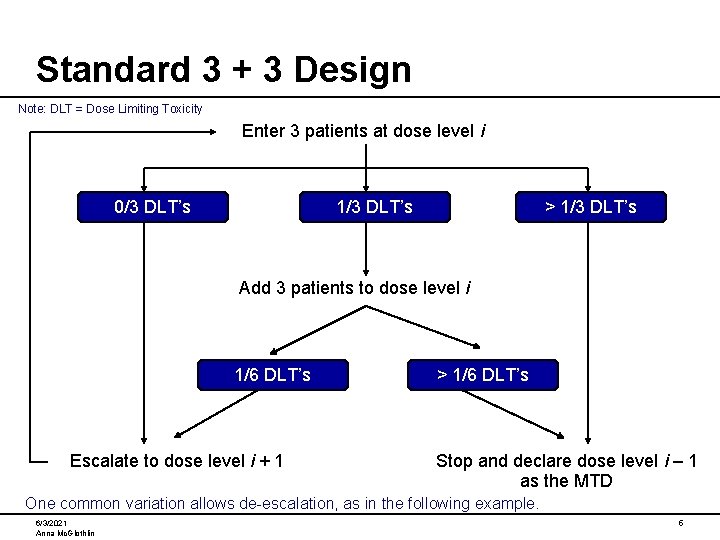
Standard 3 + 3 Design Note: DLT = Dose Limiting Toxicity Enter 3 patients at dose level i 0/3 DLT’s 1/3 DLT’s > 1/3 DLT’s Add 3 patients to dose level i 1/6 DLT’s Escalate to dose level i + 1 > 1/6 DLT’s Stop and declare dose level i – 1 as the MTD One common variation allows de-escalation, as in the following example. 6/3/2021 Anna Mc. Glothlin 5

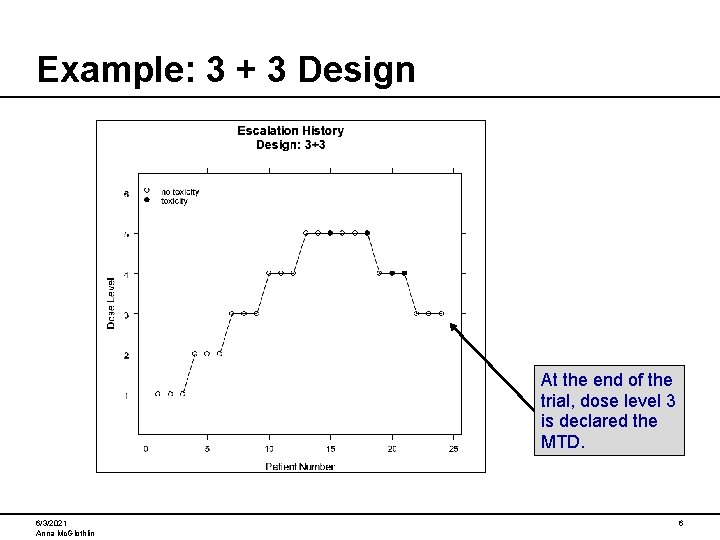
Example: 3 + 3 Design At the end of the trial, dose level 3 is declared the MTD. 6/3/2021 Anna Mc. Glothlin 6

Problems with Standard 3 + 3 Design The 3 + 3 design tends to treat a high proportion of patients at low, possibly ineffective dose levels. There is no statistical estimation of the MTD. If a dose has true DLT rate of 25%, there is a 60% chance that the algorithm will escalate to a higher dose for the next cohort. The probability of stopping at an incorrect dose level is higher than generally believed (Reiner, Paoletti, O’Quigley 1999). This design uses data only from the most recent cohort, and ignores data from previous cohorts. 6/3/2021 Anna Mc. Glothlin 7

Model-based Designs Model-based designs use a statistical model to describe the relationship between dose and outcome: Continual Reassessment Method (CRM) • O’Quigley, Pepe, Fisher (1990) • Faries (1994) • Goodman, Zahurak, Piantadosi (1995) Escalation with Overdose Control (EWOC) • Babb, Rogatko, Zacks (1998) Joint Toxicity/Efficacy • Braun (2002) • Thall and Cook (2004) 6/3/2021 Anna Mc. Glothlin 8

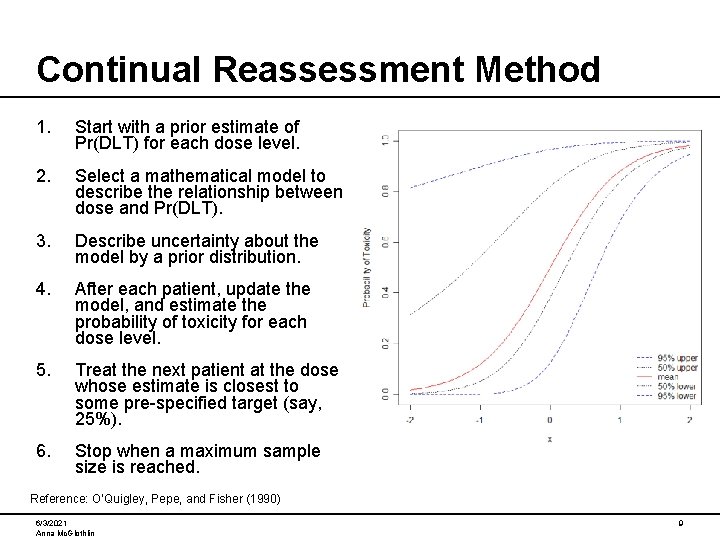
Continual Reassessment Method 1. Start with a prior estimate of Pr(DLT) for each dose level. 2. Select a mathematical model to describe the relationship between dose and Pr(DLT). 3. Describe uncertainty about the model by a prior distribution. 4. After each patient, update the model, and estimate the probability of toxicity for each dose level. 5. Treat the next patient at the dose whose estimate is closest to some pre-specified target (say, 25%). 6. Stop when a maximum sample size is reached. Reference: O’Quigley, Pepe, and Fisher (1990) 6/3/2021 Anna Mc. Glothlin 9

Statistical Models for CRM Let the toxicity response be yj ~ Binomial(nj, pj) for doses j = 1, …, J. The following models are commonly used with CRM: Hyperbolic Tangent: Logistic: Power: Prior for β: Unit Exponential, Uniform, Gamma, etc. 6/3/2021 Anna Mc. Glothlin 10

Transformation of Dose Levels These single-parameter curves are only defined over a restricted set of x’s. Therefore, the doses must be transformed to ensure that they lie in the appropriate range. The x-hat values are calculated to give the defined prior probabilities on the dose-toxicity curve, assuming that β = 1 (its prior mean) Dose Level 1 2 3 4 5 6 Prior 0. 01 0. 05 0. 15 0. 30 0. 45 0. 65 X-hat -2. 30 -1. 47 -0. 88 -0. 42 -0. 10 0. 31 6/3/2021 Anna Mc. Glothlin 11

Modifications to the CRM To address concerns surrounding the original implementation of CRM, several modifications have been proposed, including: 1. Always start at the lowest dose level. 2. Limit the escalation increment. 3. Escalate by cohorts rather than single patients. 4. Definition of MTD: • • Dose whose Pr(DLT) is closest to target, or Highest dose where Pr(DLT) is below target 5. Early stopping rules • • • Stop if CRM recommends a dose level at which XX number of cohorts have already been treated. Stop if any dose has probability > XX of being the MTD. Stop if the (1 – α)*100% credible interval for MTD is sufficiently narrow. Notable references: Faries (1994); Goodman, Zahurak, Piantadosi (1995) 6/3/2021 Anna Mc. Glothlin 12

A Hypothetical Trial Consider a dose escalation study with the following design characteristics: • Cohort Size = 3 subjects • Maximum Sample Size = 10 cohorts (30 subjects) • 6 Dose Levels • Doses must be explored in sequential order (no skipping), starting with the lowest dose. • MTD is defined as the dose level at which the probability of DLT is nearest to 25%. • Early Stopping Rule: Stop if 3 cohorts have been treated at a dose, and CRM predicts the same dose for the next cohort • Model: Hyperbolic tangent; Unit exponential prior for β • Prior Probability of DLT at each dose: Dose Level Pr(DLT) 6/3/2021 Anna Mc. Glothlin 1 2 3 4 5 6 0. 01 0. 05 0. 15 0. 30 0. 45 0. 65 13

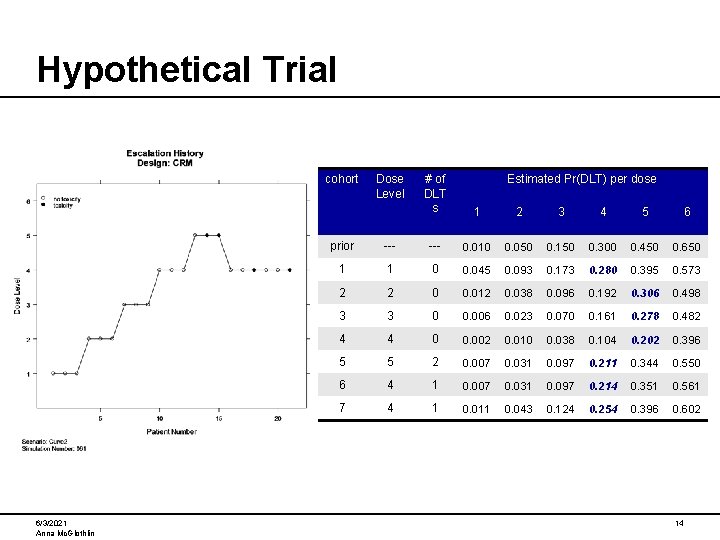
Hypothetical Trial cohort 6/3/2021 Anna Mc. Glothlin Dose Level # of DLT s Estimated Pr(DLT) per dose 1 2 3 4 5 6 prior --- 0. 010 0. 050 0. 150 0. 300 0. 450 0. 650 1 1 0 0. 045 0. 093 0. 173 0. 280 0. 395 0. 573 2 2 0 0. 012 0. 038 0. 096 0. 192 0. 306 0. 498 3 3 0 0. 006 0. 023 0. 070 0. 161 0. 278 0. 482 4 4 0 0. 002 0. 010 0. 038 0. 104 0. 202 0. 396 5 5 2 0. 007 0. 031 0. 097 0. 211 0. 344 0. 550 6 4 1 0. 007 0. 031 0. 097 0. 214 0. 351 0. 561 7 4 1 0. 011 0. 043 0. 124 0. 254 0. 396 0. 602 14

Simulation Overview The preceding slide demonstrated the performance of CRM for a single hypothetical trial. We now ask the question: “How does the method perform on average? ” This question is addressed by simulation: 1. 2. 3. Assume we know the ‘true’ curve Conduct a hypothetical trial using data generated from the true curve Repeat many times Operating Characteristics: 1. 2. 3. 6/3/2021 Anna Mc. Glothlin How often is each dose level chosen as MTD at the end of the trial? Average sample size (overall and per dose level) Etc. 15

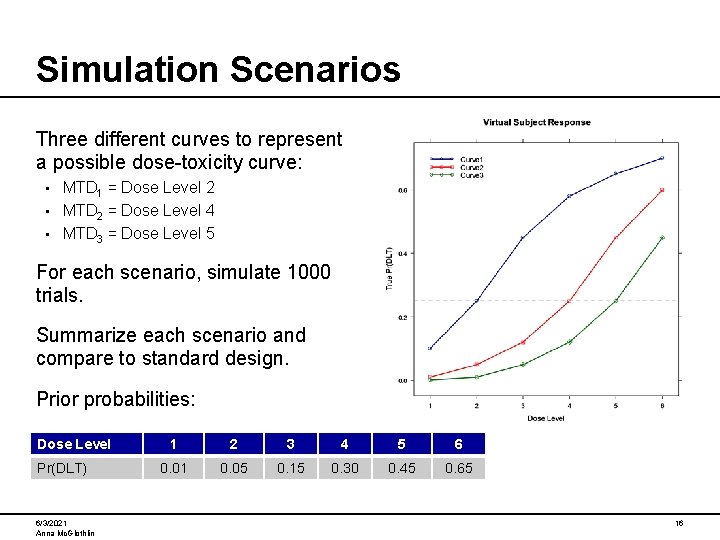
Simulation Scenarios Three different curves to represent a possible dose-toxicity curve: MTD 1 = Dose Level 2 • MTD 2 = Dose Level 4 • MTD 3 = Dose Level 5 • For each scenario, simulate 1000 trials. Summarize each scenario and compare to standard design. Prior probabilities: Dose Level Pr(DLT) 6/3/2021 Anna Mc. Glothlin 1 2 3 4 5 6 0. 01 0. 05 0. 15 0. 30 0. 45 0. 65 16

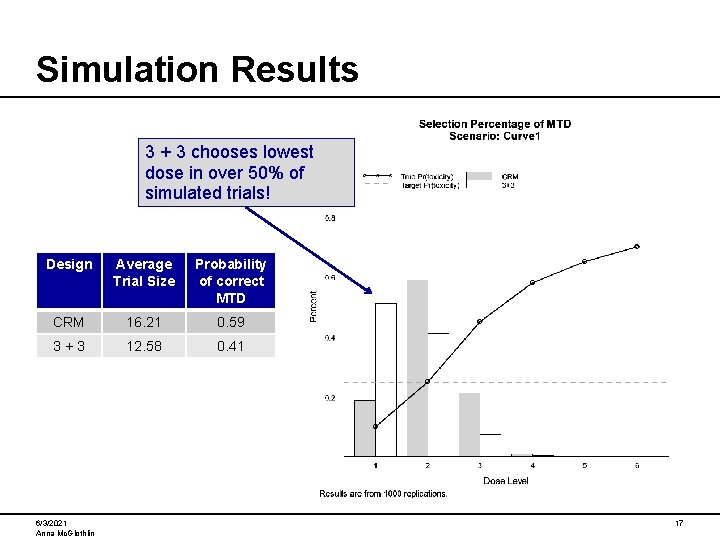
Simulation Results 3 + 3 chooses lowest dose in over 50% of simulated trials! Design Average Trial Size Probability of correct MTD CRM 16. 21 0. 59 3+3 12. 58 0. 41 6/3/2021 Anna Mc. Glothlin 17

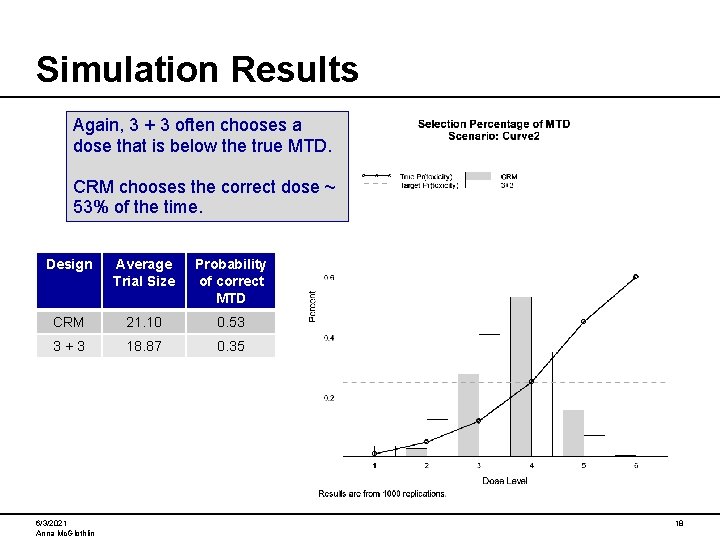
Simulation Results Again, 3 + 3 often chooses a dose that is below the true MTD. CRM chooses the correct dose ~ 53% of the time. Design Average Trial Size Probability of correct MTD CRM 21. 10 0. 53 3+3 18. 87 0. 35 6/3/2021 Anna Mc. Glothlin 18

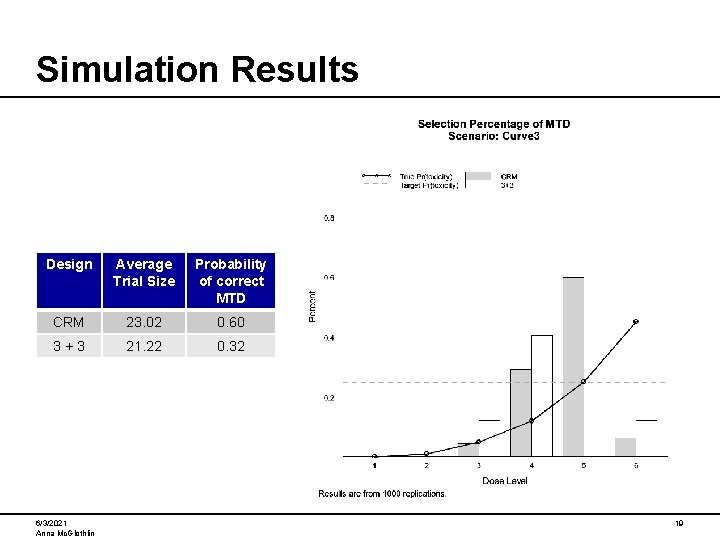
Simulation Results Design Average Trial Size Probability of correct MTD CRM 23. 02 0. 60 3+3 21. 22 0. 32 6/3/2021 Anna Mc. Glothlin 19

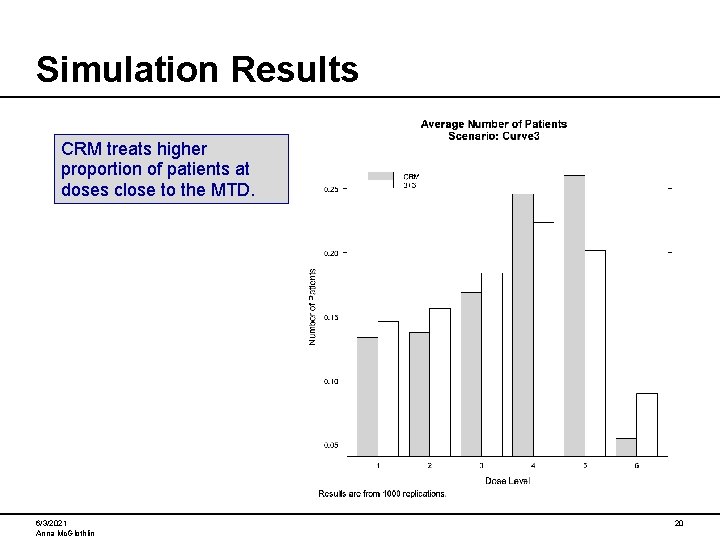
Simulation Results CRM treats higher proportion of patients at doses close to the MTD. 6/3/2021 Anna Mc. Glothlin 20

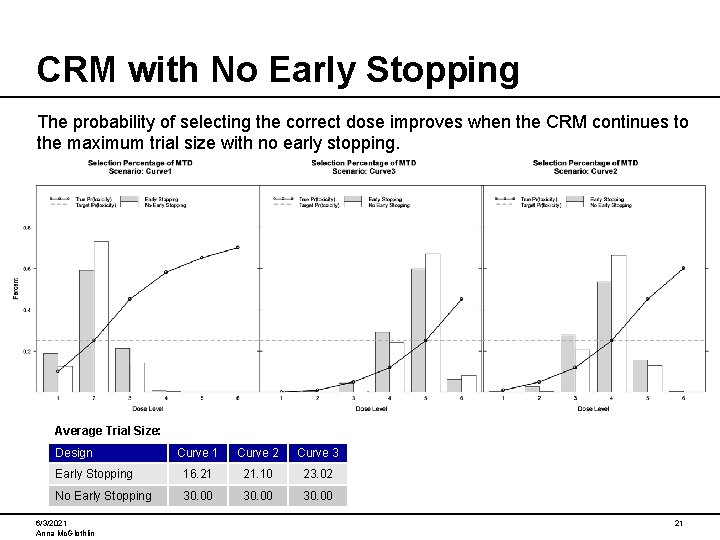
CRM with No Early Stopping The probability of selecting the correct dose improves when the CRM continues to the maximum trial size with no early stopping. Average Trial Size: Design Curve 1 Curve 2 Curve 3 Early Stopping 16. 21 21. 10 23. 02 No Early Stopping 30. 00 6/3/2021 Anna Mc. Glothlin 21

CRM vs. 3+3 1. The standard design is easy to understand implement. 2. The 3+3 design tends to choose a dose below the true MTD. 3. The CRM tends to treat patients at doses close to the MTD, whereas 3+3 treats a higher proportion of patients at low, possibly ineffective, doses. 4. The CRM provides a statistical estimate of the MTD, and allows for uncertainty around this estimate. 5. CRM can target any relevant DLT rate. 6. CRM incorporates available data from all cohorts, while the 3 + 3 design uses information from only the most recent cohort. 6/3/2021 Anna Mc. Glothlin 22

Operational considerations Allow sufficient time prior to protocol approval to conduct simulations and assess operating characteristics. Statistician will need timely access to data during the trial in order to update the model. Model updates can be performed prospectively – Given the current data, what will the model-predicted dose be if: The next patient has a DLT? The next patient has no DLT? 6/3/2021 Anna Mc. Glothlin 23

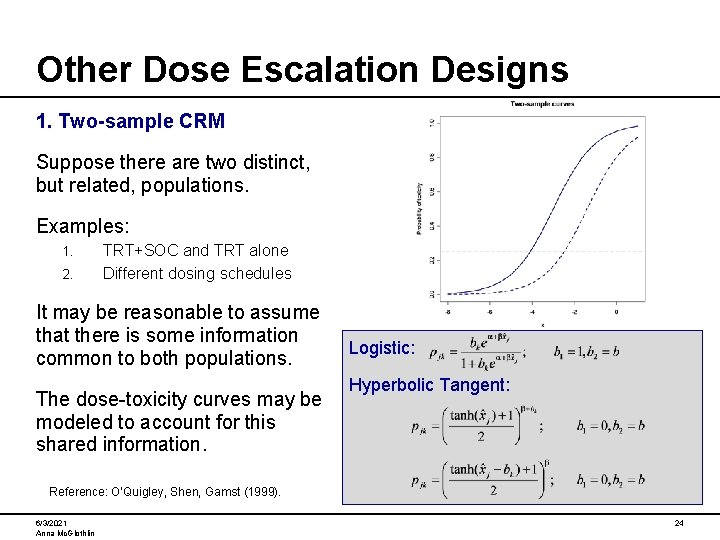
Other Dose Escalation Designs 1. Two-sample CRM Suppose there are two distinct, but related, populations. Examples: 1. 2. TRT+SOC and TRT alone Different dosing schedules It may be reasonable to assume that there is some information common to both populations. The dose-toxicity curves may be modeled to account for this shared information. Logistic: Hyperbolic Tangent: Reference: O’Quigley, Shen, Gamst (1999). 6/3/2021 Anna Mc. Glothlin 24

Other DE Designs (continued) 2. Escalation with Overdose Control (EWOC) Model: Reparameterization: where: γ = MTD ρ0 = Pr(DLT) at xmin Marginal posterior cdf of the MTD: Πk(x) Escalation Scheme: The kth patient is allocated to dose so that the posterior probability of exceeding MTD is equal to the “feasibility bound, ” α. References: Babb J, Rogatko A, Zacks S (1998); Chu et al. (2009) 6/3/2021 Anna Mc. Glothlin 25

Other DE Designs (continued) 3. Bivariate CRM Suppose that interest lies in two outcomes: toxicity and efficacy. Joint model: Where: p 1 and p 2 are the probabilities of toxicity and efficacy respectively • y and z binary indicators of toxicity and efficacy • k(p 1, p 2, ψ) is a normalizing constant • ψ is the probability of combined toxicity and efficacy. • Two-stage design: 1. Estimate MTD using the previously described CRM. 2. Then subjects are allocated to the dose whose probability of efficacy is closest to some pre-defined target. Reference: Braun (2002); Alternative design for toxicity and efficacy outcomes: Thall and Cook (2004). 6/3/2021 Anna Mc. Glothlin 26

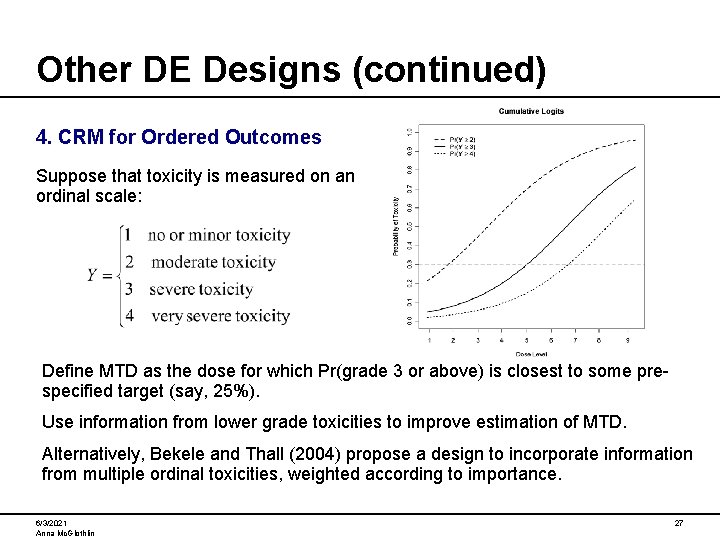
Other DE Designs (continued) 4. CRM for Ordered Outcomes Suppose that toxicity is measured on an ordinal scale: Define MTD as the dose for which Pr(grade 3 or above) is closest to some prespecified target (say, 25%). Use information from lower grade toxicities to improve estimation of MTD. Alternatively, Bekele and Thall (2004) propose a design to incorporate information from multiple ordinal toxicities, weighted according to importance. 6/3/2021 Anna Mc. Glothlin 27

Summary Traditional designs for dose escalation are not optimal for selection of MTD, and may expose a high proportion of patients to low doses. Novel designs such as CRM are under-utilized, and should be considered for dose escalation studies. Novel designs have been proposed to address different trial objectives (efficacy/toxicity, two-samples, etc. ) Simulations are vital to understanding the operating characteristics of the trial design. The most common implementation of CRM is for phase 1 oncology trials. But its use should not be confined to just one therapeutic area. • Trial design may be modified to allow a control arm: – Within each cohort, randomized subjects to TRT dose or placebo. – The placebo information may be incorporated into the dose-toxicity model. 6/3/2021 Anna Mc. Glothlin 28

Key References Bekele BN, Thall PF (2004). Dose-finding based on multiple toxicities in a soft tissue sarcoma trial. Journal of the American Statistical Association, 99: 26 -35. Babb J, Rogatko A, Zacks S (1998). Cancer phase I clinical trials: Efficient dose escalation with overdose control. Statistics in Medicine, 17: 1103 -1120. Braun TM (2002). The bivariate continual reassessment method: extending the CRM to phase I trials of two competing outcomes. Controlled Clinical Trials, 23: 240 -256. Chu P-L, Yong L, Shih WJ (2009). Unifying CRM and EWPC designs for phase I cancer clinical trials. Journal of statistical planning and inference, 139: 1146 -1163. Faries D (1994). Practical modifications of the continual reassessment method for phase I cancer clinical trials. Journal of Biopharmaceutical Statistics, 4: 147 -164. Goodman SN, Zahurak ML, Piantadosi S (1995). Some practical improvements in the continual reassessment method for phase I studies. Statistics in Medicine, 14: 1149 -1161. Heyd JM, Carlin BP (1999). Adaptive design improvements in the continual reassessment method for phase I studies. Statistics in Medicine, 18: 1307 -1321. Ishizuka N, Ohashi Y (2001). The continual reassessment method and its applications: a Bayesian methodology for phase I cancer clinical trials. Statistics in Medicine, 20: 2661 -2681. Lasonos A (2008). A comprehensive comparison of the CRM to the standard 3+3 dose escalation scheme in Phase I dose finding studies. Clinical Trials, 5: 465 -477. O’Quigley J, Pepe M, Fisher L (1990). Continual reassessment method: A practical design for phase I clinical trials in cancer. Biometrics, 46: 33 -48. O’Quigley J, Shen Z, and Gamst A (1999). Two-Sample Continual Reassessment Method. Journal of Biopharmaceutical Statistics, 9: 17 -44. Rogatko, et al. (2007). Translation of Innovative Designs Into Phase I Trials. Journal of Clinical Oncology, 25: 4982 -4986. Thall PF, Cook JD (2004). Dose-Finding Based on Efficacy-Toxicity Trade-Offs. Biometrics, 60: 684 -693. 6/3/2021 Anna Mc. Glothlin 29