BASIS BILANGAN BULAT SYAFDI MAIZORA ROSALINA BASIS BILANGAN

BASIS BILANGAN BULAT SYAFDI MAIZORA ROSALINA

BASIS BILANGAN BULAT § Teorema 3. 1 § Misalkan b suatu bilangan bulat positif yang lebih besar dari 1, maka setiap bilangan bulat positif n dapat ditulis secara tunggal dalam bentuk § dengan k suatu bilangan bulat taknegatif, aj suatu bilangan bulat dengan 0 < aj < b-1 untuk j=0, 1, 2, …k dengan ak≠ 0.

Jika n dapat dituliskan dalam maka n dapat ditulis dalam basis b yakni,

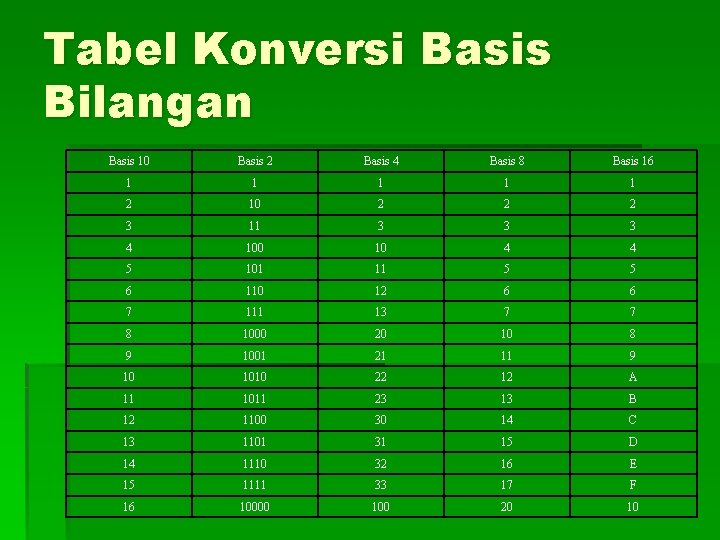
Tabel Konversi Basis Bilangan Basis 10 Basis 2 Basis 4 Basis 8 Basis 16 1 1 1 2 10 2 2 2 3 11 3 3 3 4 100 10 4 4 5 101 11 5 5 6 110 12 6 6 7 111 13 7 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 12 1100 30 14 C 13 1101 31 15 D 14 1110 32 16 E 15 1111 33 17 F 16 10000 100 20 10

penggunaannya § Mengubah basis 2 ke basis 8 adalah dengan mengelompokan basis 2 dalam tiga angka-tiga angka dari kanan. Selanjutnya ganti tiap kelompok tersebut dengan angka yang sesuai pada tabel basis 8. sebaliknya, dari basis 8 ke basis 2, ganti angka-angka pada lambang bilangan basis 8 dengan angka-angka basis 2 dengan catatan tiap angka pada basis 8 disediakan tiga tempat pada basis 2. § Mengubah basis 2 ke basis 4 adalah dengan mengelompokan basis 2 dalam dua angka-dua angka dari kanan. Selanjutnya ganti tiap kelompok tersebut dengan angka yang sesuai pada tabel basis 4. sebaliknya, dari basis 4 ke basis 2, ganti angka-angka pada lambang bilangan basis 4 dengan angka-angka basis 2 dengan catatan tiap angka pada basis 4 disediakan dua tempat pada basis 2. § Mengubah basis 2 ke basis 16 adalah dengan mengelompokan basis 2 dalam empat angka-empat angka dari kanan. Selanjutnya ganti tiap kelompok tersebut dengan angka yang sesuai pada tabel basis 16. sebaliknya, dari basis 16 ke basis 2, ganti angka-angka pada lambang bilangan basis 16 dengan angka-angka basis 2 dengan catatan tiap angka pada basis 16 disediakan empat tempat pada basis 2. § Begitu juga dengan mengubah basis 3 ke basis 9, 4 ke 16 atau sebaliknya. Secara umum cara tersebut dapat digunakan untuk mengubah basis k ke kt atau sebaliknya dengan k dan t adalah bilangan asli dan k tidak sama dengan 1.

Contoh 1 § Misalkan suatu bilangan bulat n dinyatakan sebagai § n = 3. 54 +2. 53 +0. 52 +1. 5 +4 § maka n = 320145. tentukan n dalam basis sepuluh dan basis delapan.

Contoh 2 § Nyatakan 1001102 dalam jumlah perpangkatan bulat dari 2 dan nyatakan dalam basis sepuluh

Contoh 3 § Tulislah 116 dalam lambang bilangan dengan basis 2.

Contoh 4 § Tentukan lambang bilangan dalam basis decimal dari 2 AC 316 dan FA 016.

TERIMA KASIH