Basics of Sampling Theory P x 1 x

Basics of Sampling Theory P = { x 1, x 2, ……, x. N} where P = population x 1, x 2, ……, x. N are real numbers Assuming x is a random variable; Mean/Average of x, N x= Σ xi i=1 N

Basics of Sampling Theory Standard Deviation, √ σx = Variance, σx 2 N Σ (xi – x)2 i=1 N N = Σ (xi – x)2 i=1 N

Basics of Sampling Theory Theorem About Mean picking random numbers x, mean = x picking random numbers y, mean = y x=y Picking another number z, mean z = x = y z = c 1 x + c 2 y ; c 1, c 2 are constants z=x+y

Basics of Sampling Theory Independence two events are independent if the occurrence of one of the events gives no information about whether or not the other event will occur; that is, the events have no influence on each other for example a, b and c are independent if: - a and b are independent; a and c are independent; and b and c are independent

Basics of Sampling Theory Theorem About Variances/Sampling Theorem z = (x + y)/2; σz 2 = ? σz 2 < σx 2 Taking, z = (x + y)/2 σz 2 = (σx 2 + σy 2)/4 Taking k sample, z = (x + x’’ + …. + x’’…k)/k σz 2 = (kσx 2 )/k 2 σz 2 = σx 2 )/k * This theory works only on independent variables; while mean theorem works on dependent variable * Error depends on number of samples; bigger sample – less error; smaller sample – more error * This formula is true for sampling with replacement
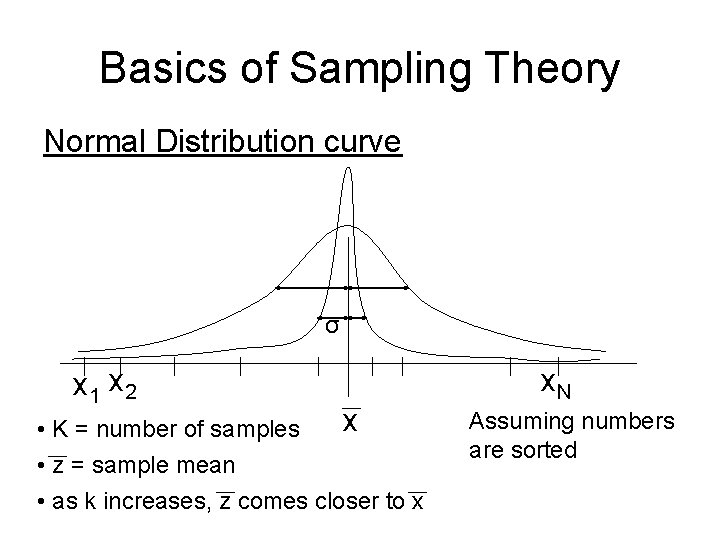
Basics of Sampling Theory Normal Distribution curve σ x 1 x 2 x • K = number of samples • z = sample mean • as k increases, z comes closer to x x. N Assuming numbers are sorted
- Slides: 6