Basics of RF Superconductivity and QCRelated Microwave Issues

Basics of RF Superconductivity and QC-Related Microwave Issues Short Course Tutorial Superconducting Quantum Computing 2014 Applied Superconductivity Conference Charlotte, North Carolina USA Steven M. Anlage Center for Nanophysics and Advanced Materials Physics Department University of Maryland College Park, MD 20742 -4111 USA anlage@umd. edu 1 Steven Anlage

Objective To give a basic introduction to superconductivity, superconducting electrodynamics, and microwave measurements as background for the Short Course Tutorial “Superconducting Quantum Computation” Electronics Sessions at ASC 2014: Digital Electronics (10 sessions) Nanowire / Kinetic Inductance / Single-photon Detectors (10 sessions) Transition-Edge Sensors / Bolometers (8 sessions) SQUIDs / Nano. SQUIDs / SQUIFs (6 sessions) Superconducting Qubits (5 sessions) Microwave / THz Applications (4 sessions) Mixers (1 session) 2 Steven Anlage

Outline • • 3 Hallmarks of Superconductivity Essentials of Superconductivity Superconducting Transmission Lines Network Analysis Superconducting Microwave Resonators for QC Microwave Losses Fundamentals of Microwave Modeling and Simulation Measurements QC-Related Microwave Technology Steven Anlage

Please Ask Questions! 4 Steven Anlage

I. Hallmarks of Superconductivity • The Three Hallmarks of Superconductivity • Zero Resistance • Complete* Diamagnetism • Macroscopic Quantum Effects • Superconductors in a Magnetic Field • Vortices and Dissipation 5 Steven Anlage I. Hallmarks of Superconductivity

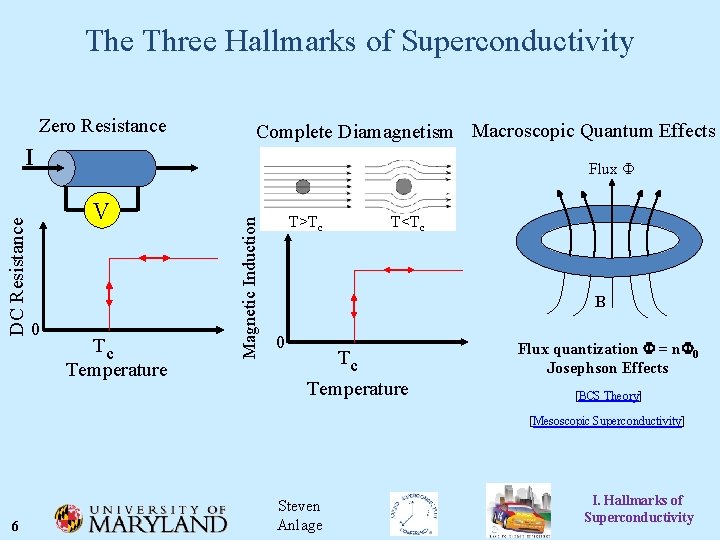
The Three Hallmarks of Superconductivity Zero Resistance Complete Diamagnetism Macroscopic Quantum Effects Flux F V 0 Tc Temperature Magnetic Induction DC Resistance I T>Tc T<Tc B 0 Flux quantization F = n. F 0 Josephson Effects Tc Temperature [BCS Theory] [Mesoscopic Superconductivity] 6 Steven Anlage I. Hallmarks of Superconductivity

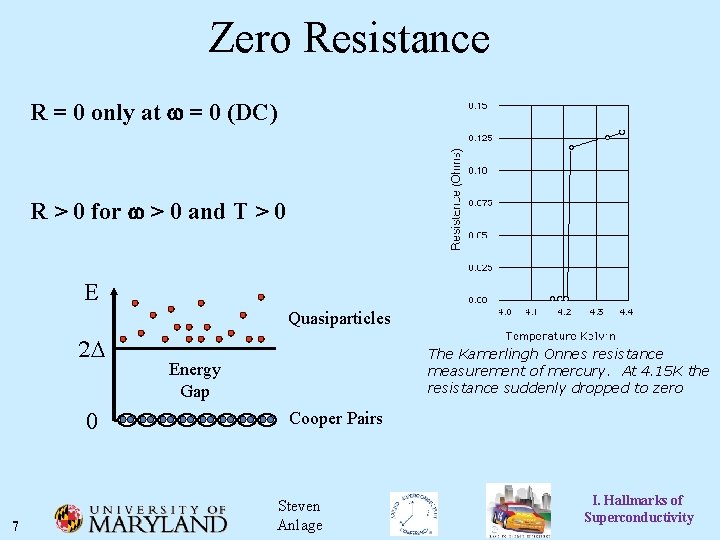
Zero Resistance R = 0 only at w = 0 (DC) R > 0 for w > 0 and T > 0 E Quasiparticles 2 D 0 7 The Kamerlingh Onnes resistance measurement of mercury. At 4. 15 K the resistance suddenly dropped to zero Energy Gap Cooper Pairs Steven Anlage I. Hallmarks of Superconductivity

Perfect Diamagnetism Magnetic Fields and Superconductors are not generally compatible The Meissner Effect Superconductor l(T) magnetic penetration depth T>Tc vacuum l superconductor Spontaneous exclusion of magnetic flux B=0 l surface screening currents l(0) l is independent of frequency (w < 2 D/ħ) 8 T<Tc T Tc Steven Anlage The Yamanashi MLX 01 Mag. Lev test vehicle achieved a speed of 361 mph (581 kph) in 2003 I. Hallmarks of Superconductivity

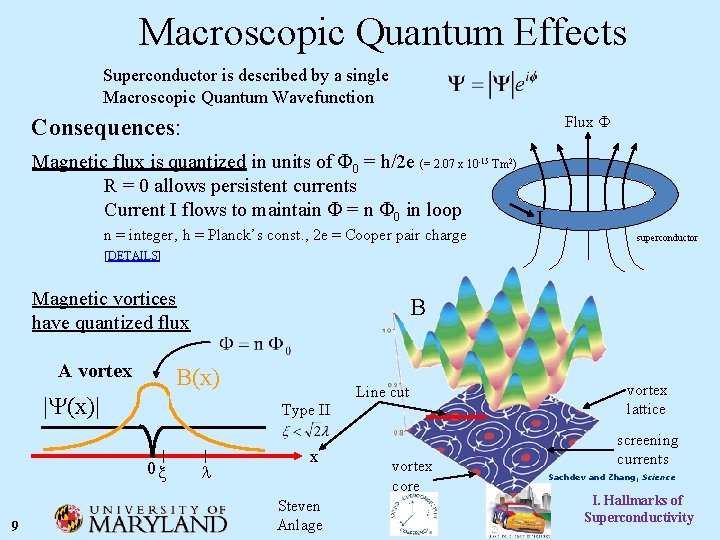
Macroscopic Quantum Effects Superconductor is described by a single Macroscopic Quantum Wavefunction Flux F Consequences: Magnetic flux is quantized in units of F 0 = h/2 e (= 2. 07 x 10 R = 0 allows persistent currents Current I flows to maintain F = n F 0 in loop n = integer, h = Planck’s const. , 2 e = Cooper pair charge [DETAILS] Magnetic vortices have quantized flux A vortex Line cut Type II 0 x l x Steven Anlage vortex core I superconductor B B(x) |Y(x)| 9 -15 Tm 2) vortex lattice screening currents Sachdev and Zhang, Science I. Hallmarks of Superconductivity

Definition of “Flux” surface 10 surface Steven Anlage I. Hallmarks of Superconductivity

Macroscopic Quantum Effects Continued Josephson Effects (Tunneling of Cooper Pairs) DC Josephson Effect (VDC=0) 2 1 I AC Josephson Effect (VDC 0) (Tunnel barrier) VDC Gauge-invariant phase difference: Quantum VCO: [DC SQUID Detail] 11 Steven Anlage [RF SQUID Detail] I. Hallmarks of Superconductivity

Superconductors in a Magnetic Field The Vortex State H Hc 2(0) Normal State Lorentz Force B 0, R 0 vortex Abrikosov Vortex Lattice Hc 1(0) B = 0, R = 0 Meissner State Type II SC Tc T Moving vortices create a longitudinal voltage I V>0 [Phase diagram Details] 12 Vortices also experience a viscous drag force: Steven Anlage I. Hallmarks of Superconductivity

II. Superconducting Transmission Lines • Property I: Low-Loss • Two-Fluid Model • Surface Impedance and Complex Conductivity [Details] • BCS Electrodynamics [Details] • Property II: Low-Dispersion • Kinetic Inductance • Josephson Inductance 13 Steven Anlage II. Superconducting Transmission Lines

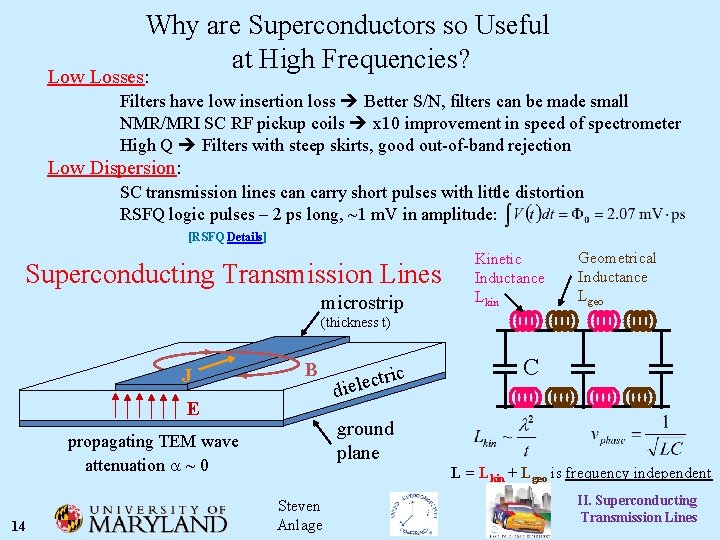
Why are Superconductors so Useful at High Frequencies? Low Losses: Filters have low insertion loss Better S/N, filters can be made small NMR/MRI SC RF pickup coils x 10 improvement in speed of spectrometer High Q Filters with steep skirts, good out-of-band rejection Low Dispersion: SC transmission lines can carry short pulses with little distortion RSFQ logic pulses – 2 ps long, ~1 m. V in amplitude: [RSFQ Details] Superconducting Transmission Lines microstrip Kinetic Inductance Lkin Geometrical Inductance Lgeo (thickness t) J B E C ground plane propagating TEM wave attenuation a ~ 0 14 ric t c e l die L = Lkin + Lgeo is frequency independent Steven Anlage II. Superconducting Transmission Lines

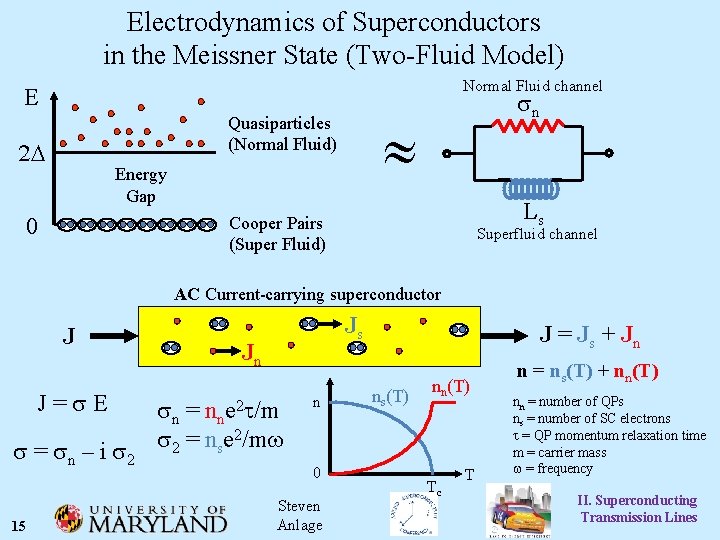
Electrodynamics of Superconductors in the Meissner State (Two-Fluid Model) Normal Fluid channel E Quasiparticles (Normal Fluid) 2 D Energy Gap 0 sn Ls Cooper Pairs (Super Fluid) Superfluid channel AC Current-carrying superconductor J J = s E s = sn – i s 2 15 Js Jn sn = nne 2 t/m s 2 = nse 2/mw ns(T) n 0 Steven Anlage J = Js + Jn nn(T) Tc T n = ns(T) + nn(T) nn = number of QPs ns = number of SC electrons t = QP momentum relaxation time m = carrier mass w = frequency II. Superconducting Transmission Lines

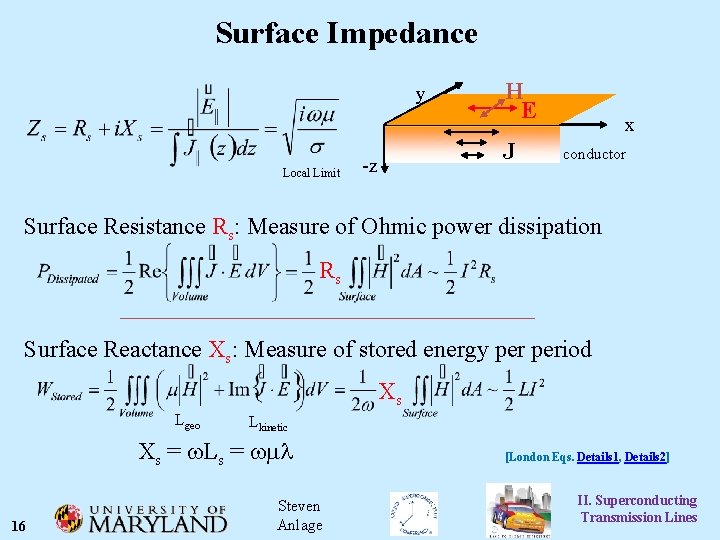
Surface Impedance y Local Limit H E J -z x conductor Surface Resistance Rs: Measure of Ohmic power dissipation Rs Surface Reactance Xs: Measure of stored energy period Xs Lgeo Lkinetic Xs = w. Ls = wml 16 Steven Anlage [London Eqs. Details 1, Details 2] II. Superconducting Transmission Lines

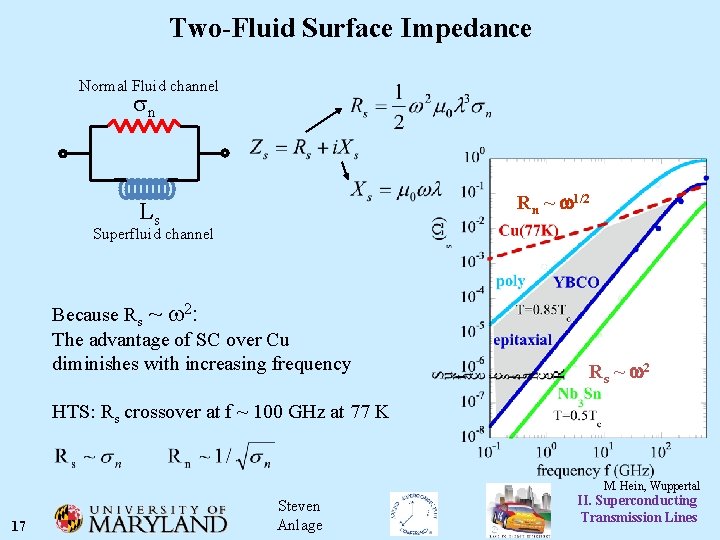
Two-Fluid Surface Impedance Normal Fluid channel sn Rn ~ w 1/2 Ls Superfluid channel Because Rs ~ w 2: The advantage of SC over Cu diminishes with increasing frequency R s ~ w 2 HTS: Rs crossover at f ~ 100 GHz at 77 K M. Hein, Wuppertal 17 Steven Anlage II. Superconducting Transmission Lines

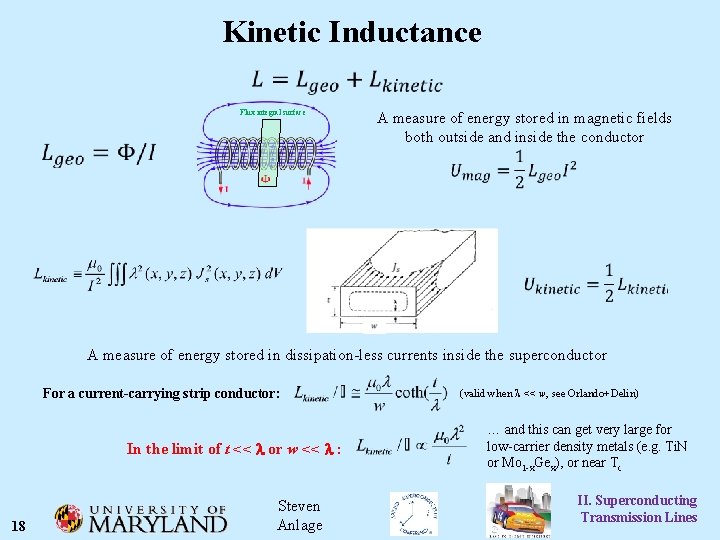
Kinetic Inductance Flux integral surface A measure of energy stored in magnetic fields both outside and inside the conductor A measure of energy stored in dissipation-less currents inside the superconductor For a current-carrying strip conductor: (valid when l << w, see Orlando+Delin) … and this can get very large for low-carrier density metals (e. g. Ti. N or Mo 1 -x. Gex), or near Tc In the limit of t << l or w << l : 18 Steven Anlage II. Superconducting Transmission Lines

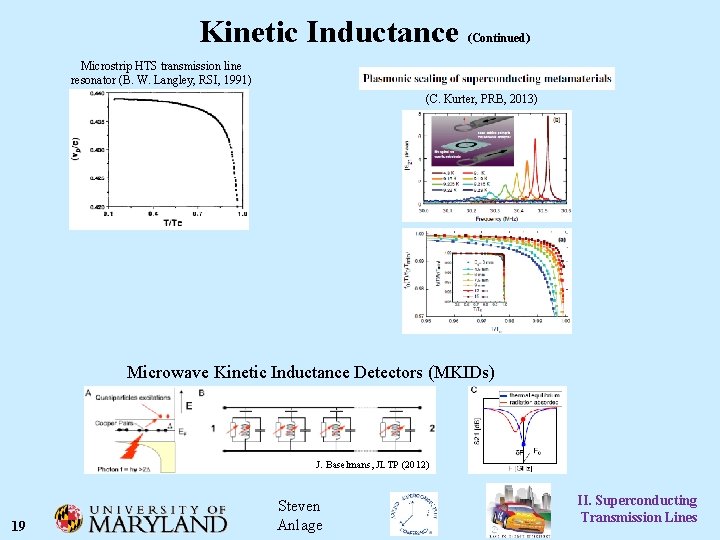
Kinetic Inductance (Continued) Microstrip HTS transmission line resonator (B. W. Langley, RSI, 1991) (C. Kurter, PRB, 2013) Microwave Kinetic Inductance Detectors (MKIDs) J. Baselmans, JLTP (2012) 19 Steven Anlage II. Superconducting Transmission Lines

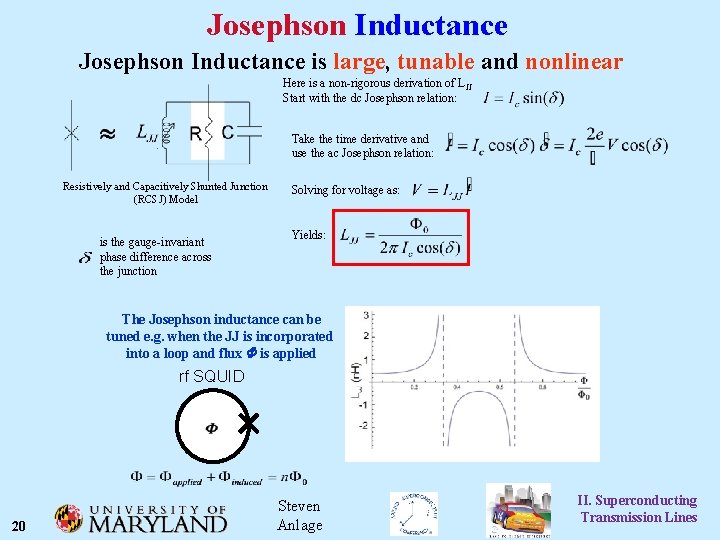
Josephson Inductance is large, tunable and nonlinear Here is a non-rigorous derivation of L JJ Start with the dc Josephson relation: Take the time derivative and use the ac Josephson relation: Resistively and Capacitively Shunted Junction (RCSJ) Model is the gauge-invariant phase difference across the junction Solving for voltage as: Yields: The Josephson inductance can be tuned e. g. when the JJ is incorporated into a loop and flux F is applied rf SQUID 20 Steven Anlage II. Superconducting Transmission Lines

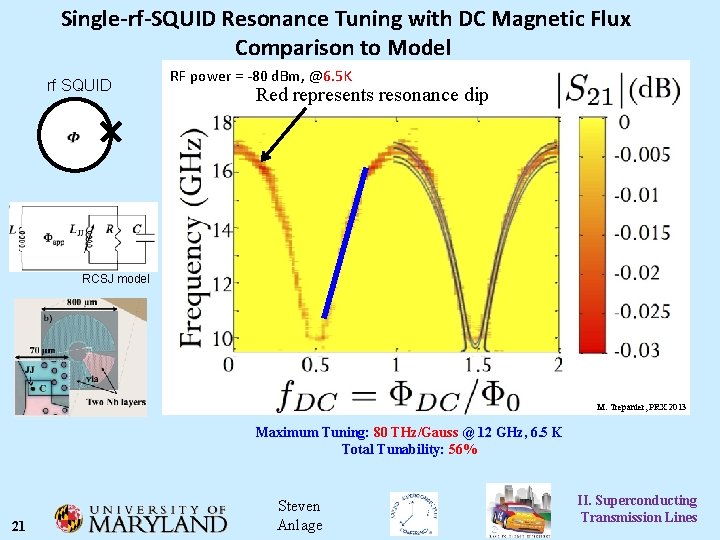
Single-rf-SQUID Resonance Tuning with DC Magnetic Flux Comparison to Model rf SQUID RF power = -80 d. Bm, @6. 5 K Red represents resonance dip RCSJ model M. Trepanier, PRX 2013 Maximum Tuning: 80 THz/Gauss @ 12 GHz, 6. 5 K Total Tunability: 56% 21 Steven Anlage II. Superconducting Transmission Lines

22 Steven Anlage

III. Network Analysis • Network vs. Spectrum Analysis • Scattering (S) Parameters • Quality Factor Q • Cavity Perturbation Theory [Details] 23 Steven Anlage III. Network Analysis

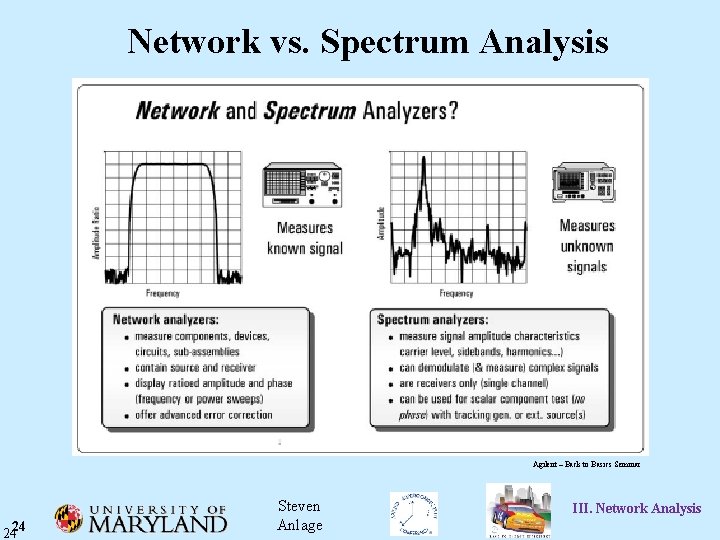
Network vs. Spectrum Analysis Agilent – Back to Basics Seminar 2424 Steven Anlage III. Network Analysis

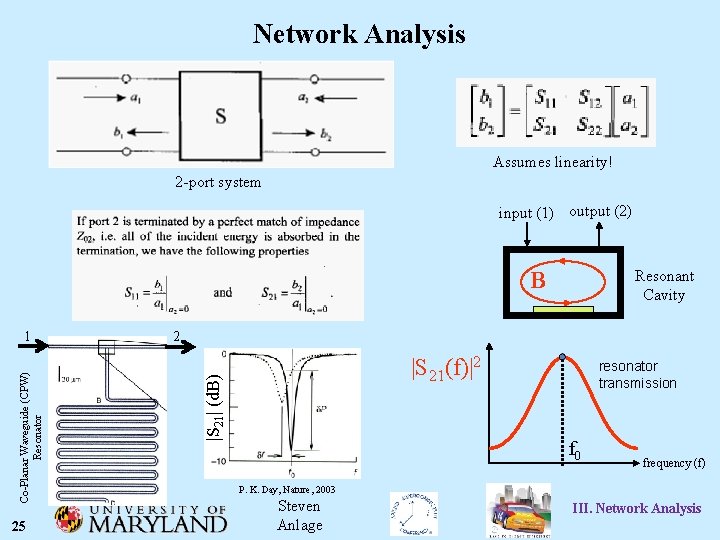
Network Analysis Assumes linearity! 2 -port system input (1) output (2) Resonant Cavity B 25 2 |S 21(f)|2 |S 21| (d. B) Co-Planar Waveguide (CPW) Resonator 1 resonator transmission f 0 frequency (f) P. K. Day, Nature, 2003 Steven Anlage III. Network Analysis

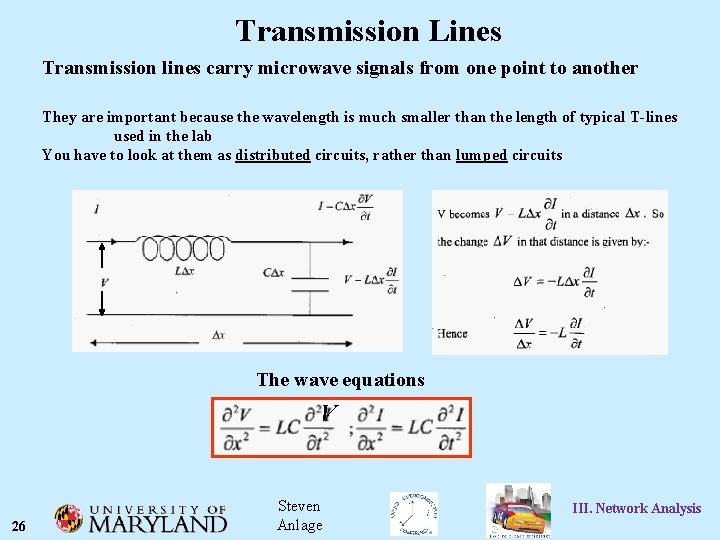
Transmission Lines Transmission lines carry microwave signals from one point to another They are important because the wavelength is much smaller than the length of typical T-lines used in the lab You have to look at them as distributed circuits, rather than lumped circuits The wave equations V 26 Steven Anlage III. Network Analysis

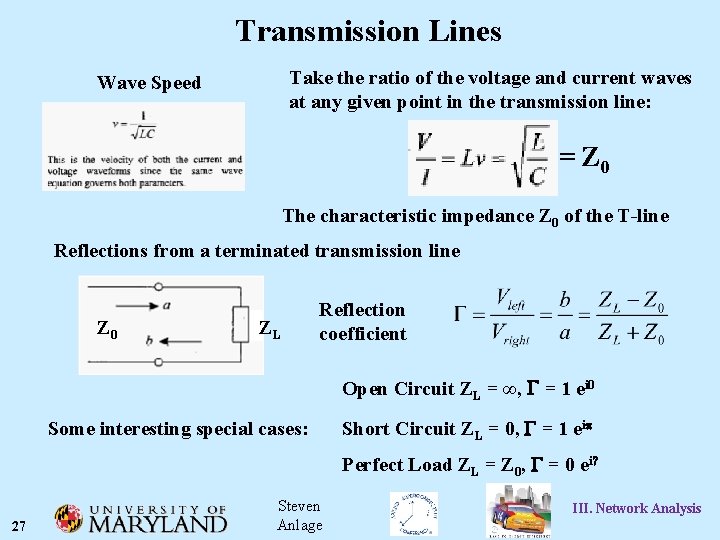
Transmission Lines Take the ratio of the voltage and current waves at any given point in the transmission line: Wave Speed = Z 0 The characteristic impedance Z 0 of the T-line Reflections from a terminated transmission line Z 0 ZL Reflection coefficient Open Circuit ZL = ∞, G = 1 ei 0 Some interesting special cases: Short Circuit ZL = 0, G = 1 eip Perfect Load ZL = Z 0, G = 0 ei? 27 Steven Anlage III. Network Analysis

Transmission Lines and Their Characteristic Impedances [Transmission Line Detail] Normalized Values Attenuation is lowest at 77 W 28 Steven Anlage 50 W Standard Power handling capacity peaks at 30 W Characteristic Impedance for coaxial cable (W) 28 Agilent – Back to Basics Seminar

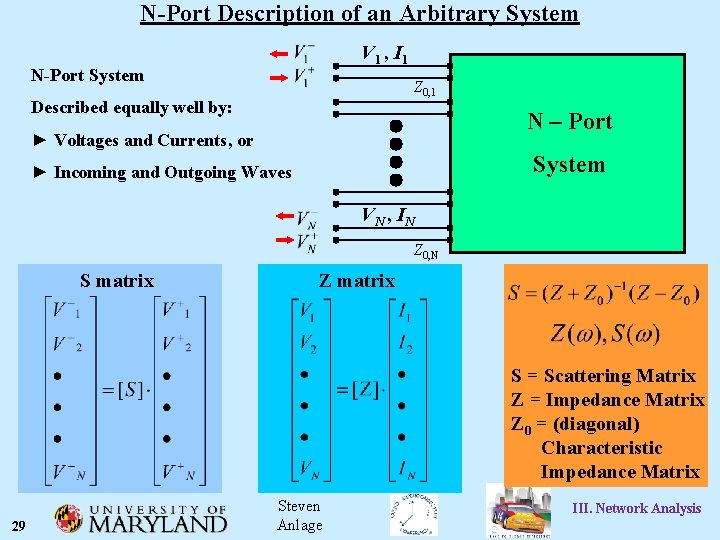
N-Port Description of an Arbitrary System V 1 , I 1 N-Port System Z 0, 1 Described equally well by: N – Port ► Voltages and Currents, or System ► Incoming and Outgoing Waves V N , IN Z 0, N S matrix Z matrix S = Scattering Matrix Z = Impedance Matrix Z 0 = (diagonal) Characteristic Impedance Matrix 29 Steven Anlage III. Network Analysis

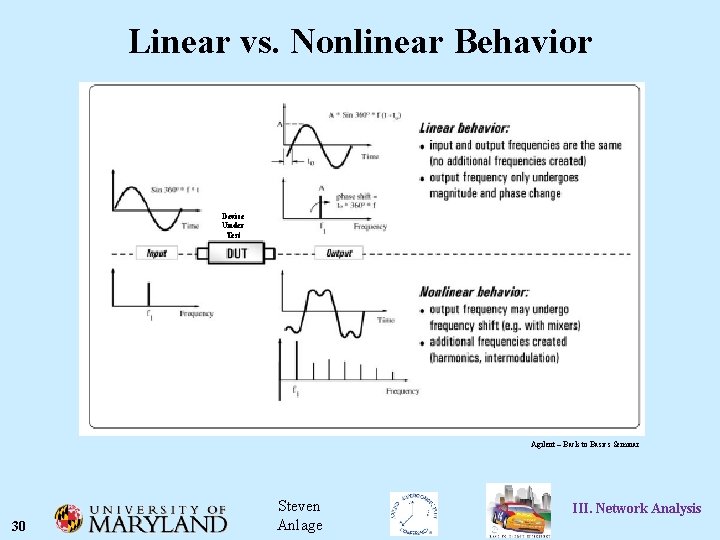
Linear vs. Nonlinear Behavior Device Under Test Agilent – Back to Basics Seminar 30 Steven Anlage III. Network Analysis

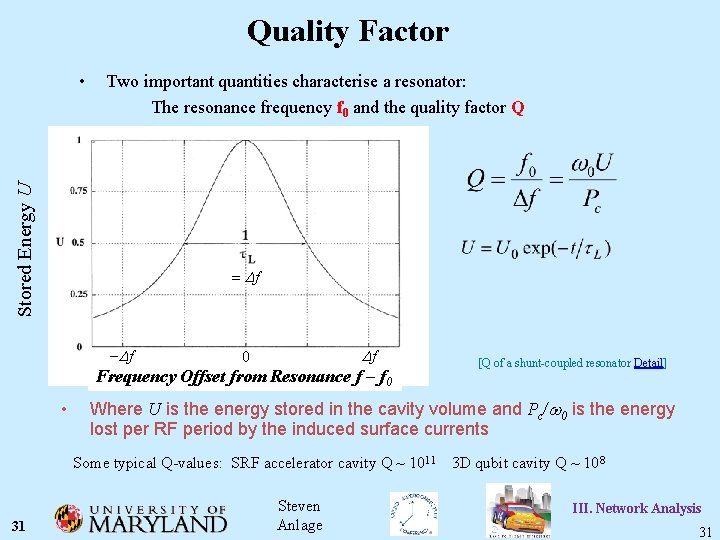
Quality Factor Two important quantities characterise a resonator: The resonance frequency f 0 and the quality factor Q Stored Energy U • = Df -Df Df 0 Frequency Offset from Resonance f – f 0 • [Q of a shunt-coupled resonator Detail] Where U is the energy stored in the cavity volume and Pc/ 0 is the energy lost per RF period by the induced surface currents Some typical Q-values: SRF accelerator cavity Q ~ 1011 3 D qubit cavity Q ~ 108 31 Steven Anlage III. Network Analysis 31

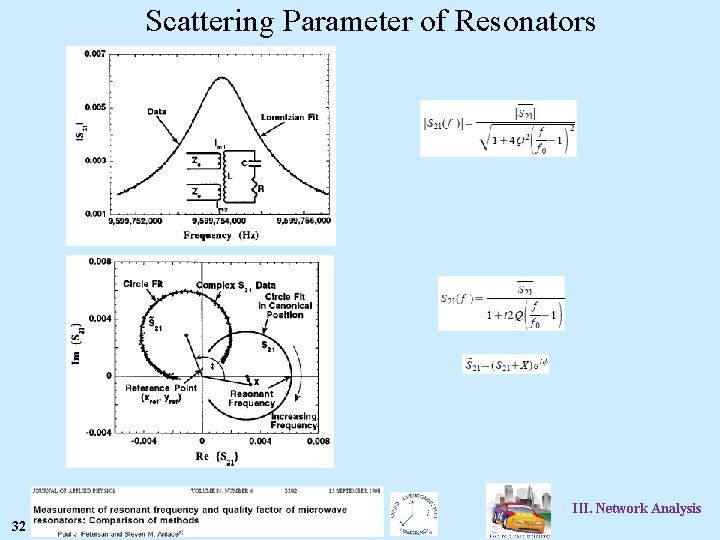
Scattering Parameter of Resonators 32 Steven Anlage III. Network Analysis

IV. Superconducting Microwave Resonators for QC • Thin Film Resonators • Co-planar Waveguide • Lumped-Element • SQUID-based • Bulk Resonators • Coupling to Resonators 33 Steven Anlage IV. Superconducting Microwave Resonators for QC

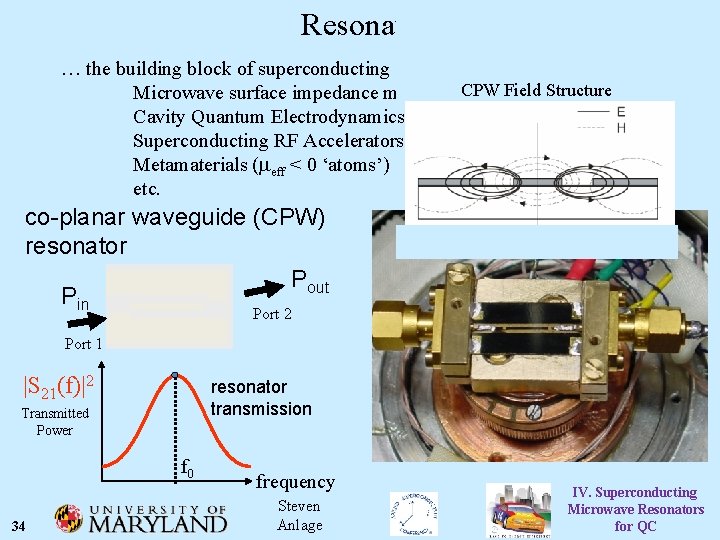
Resonators … the building block of superconducting applications … CPW Field Structure Microwave surface impedance measurements Cavity Quantum Electrodynamics of Qubits Superconducting RF Accelerators Metamaterials (meff < 0 ‘atoms’) etc. co-planar waveguide (CPW) resonator Pout Pin Port 2 Port 1 |S 21(f)|2 resonator transmission Transmitted Power f 0 34 frequency Steven Anlage IV. Superconducting Microwave Resonators for QC

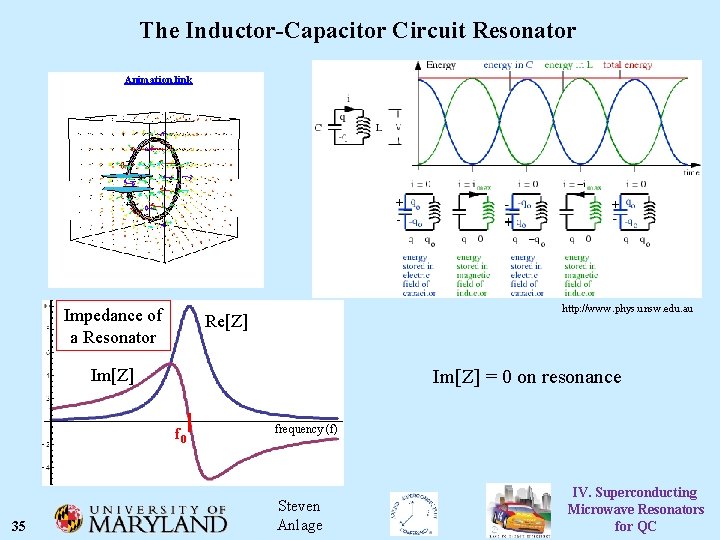
The Inductor-Capacitor Circuit Resonator Animation link Impedance of a Resonator http: //www. phys. unsw. edu. au Re[Z] Im[Z] = 0 on resonance f 0 35 frequency (f) Steven Anlage IV. Superconducting Microwave Resonators for QC

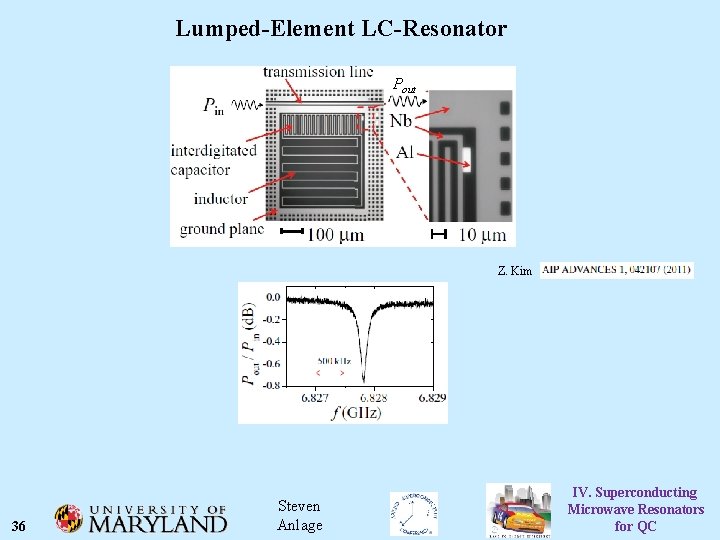
Lumped-Element LC-Resonator Pout Z. Kim 36 Steven Anlage IV. Superconducting Microwave Resonators for QC

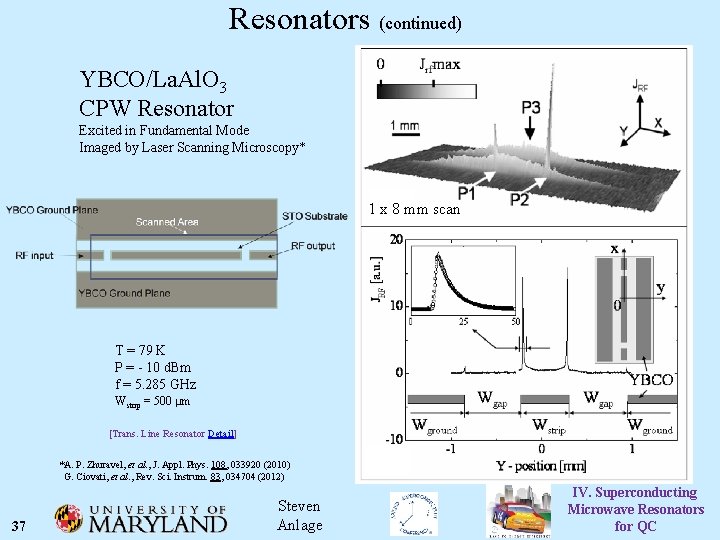
Resonators (continued) YBCO/La. Al. O 3 CPW Resonator Excited in Fundamental Mode Imaged by Laser Scanning Microscopy* 1 x 8 mm scan T = 79 K P = - 10 d. Bm f = 5. 285 GHz Wstrip = 500 mm [Trans. Line Resonator Detail] *A. P. Zhuravel, et al. , J. Appl. Phys. 108, 033920 (2010) G. Ciovati, et al. , Rev. Sci. Instrum. 83, 034704 (2012) 37 Steven Anlage IV. Superconducting Microwave Resonators for QC

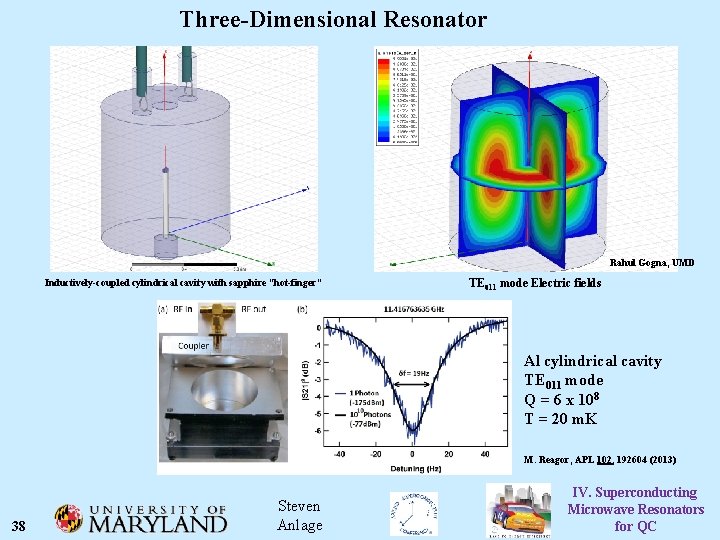
Three-Dimensional Resonator Rahul Gogna, UMD TE 011 mode Electric fields Inductively-coupled cylindrical cavity with sapphire “hot-finger” Al cylindrical cavity TE 011 mode Q = 6 x 108 T = 20 m. K M. Reagor, APL 102, 192604 (2013) 38 Steven Anlage IV. Superconducting Microwave Resonators for QC

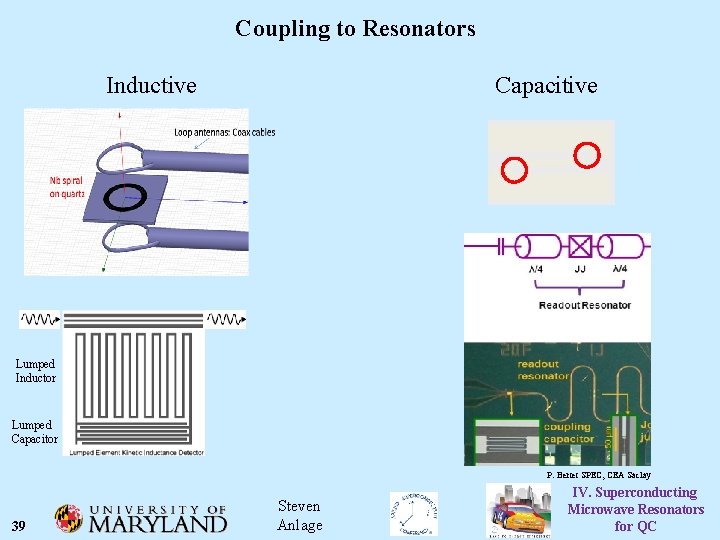
Coupling to Resonators Inductive Capacitive Lumped Inductor Lumped Capacitor P. Bertet SPEC, CEA Saclay 39 Steven Anlage IV. Superconducting Microwave Resonators for QC

V. Microwave Losses • Microscopic Sources of Loss • 2 -Level Systems (TLS) in Dielectrics • Flux Motion • What Limits the Q of Resonators? 40 Steven Anlage V. Microwave Losses

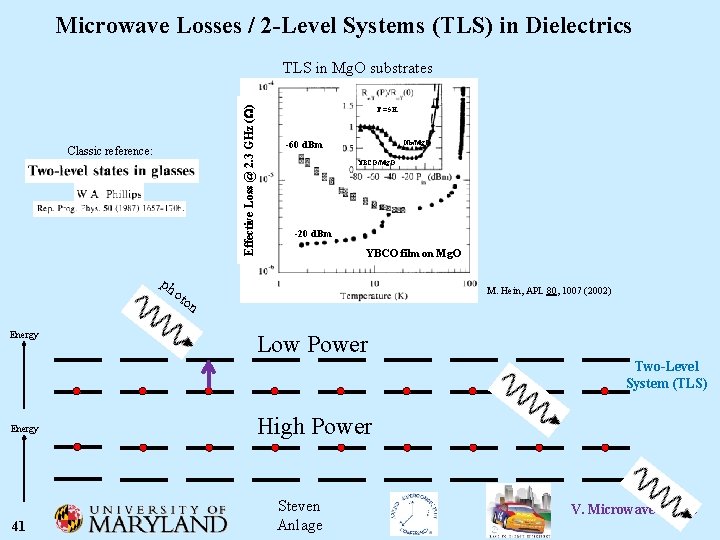
Microwave Losses / 2 -Level Systems (TLS) in Dielectrics Effective Loss @ 2. 3 GHz (W) TLS in Mg. O substrates Classic reference: T = 5 K -60 d. Bm Nb/Mg. O YBCO/Mg. O -20 d. Bm YBCO film on Mg. O ph oto M. Hein, APL 80, 1007 (2002) n Energy Low Power Two-Level System (TLS) Energy 41 High Power Steven Anlage V. Microwave Losses

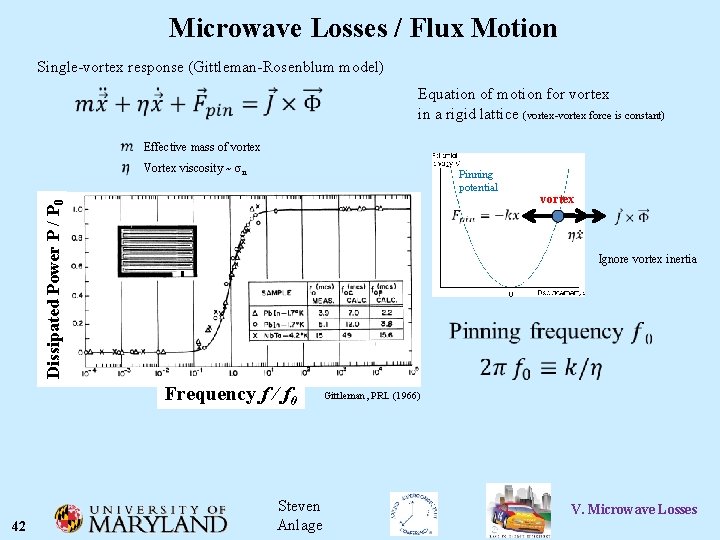
Microwave Losses / Flux Motion Single-vortex response (Gittleman-Rosenblum model) Equation of motion for vortex in a rigid lattice (vortex-vortex force is constant) Effective mass of vortex Vortex viscosity ~ sn Pinning potential Dissipated Power P / P 0 Ignore vortex inertia Frequency f / f 0 42 vortex Steven Anlage Gittleman, PRL (1966) V. Microwave Losses

What Limits the Q of Resonators? Assumption: Loss mechanisms add linearly 43 Steven Anlage Power dissipated in load impedance(s) V. Microwave Losses

VI. Microwave Modeling and Simulation • Computational Electromagnetics (CEM) • Finite Element Approach (FEM) • Finite Difference Time Domain (FDTD) • Solvers • Eigenmode • Driven • Transient Time-Domain • Examples 44 of Use Steven Anlage VI. Microwave Modeling and Simulation

Computational EM: FEM and FDTD The Maxwell curl equations Finite Difference Time Domain (FDTD): Directly approximate the differential operators on a grid staggered in time and space. E and H computed on a regular grid and advanced in time. Finite-Element Method (FEM): Create a finite-element mesh (triangles and tetrahedra), expand the fields in a series of basis functions on the mesh, then solve a matrix equation that minimizes a variational functional corresponds to the solutions of Maxwell’s equations subject to the boundary conditions. Method Advantages Disadvantages Examples FEM Conformal meshes model curved surfaces well. Handles dispersive materials. Good for finding eigenmodes. Can be linked to other FEM solvers (thermal, mechanical, etc. ) Does not handle nonlinear materials easily. Meshes can get very large and limit the computation. Solvers are often proprietary. High Frequency Structure Simulator (HFSS) and other frequency-domain solvers, including the COMSOL RF module. FDTD 45 Handles nonlinearity and Not good for high-Q wideband signals well. devices or dispersive Less limited by mesh size materials. Staircased grid than FEM – better for does not model curved electrically-large structures. surfaces well. Easy to parallelize and Steven solve with GPUs. Anlage CST Microwave Studio, XFDTD

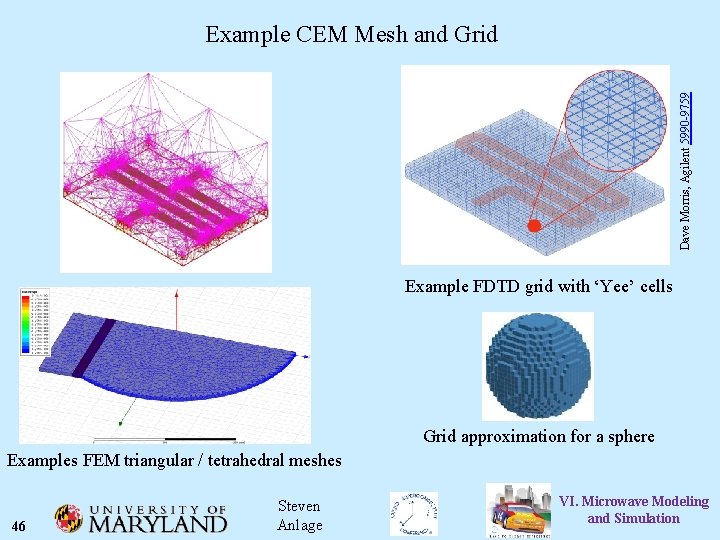
Dave Morris, Agilent 5990 -9759 Example CEM Mesh and Grid Example FDTD grid with ‘Yee’ cells Grid approximation for a sphere Examples FEM triangular / tetrahedral meshes 46 Steven Anlage VI. Microwave Modeling and Simulation

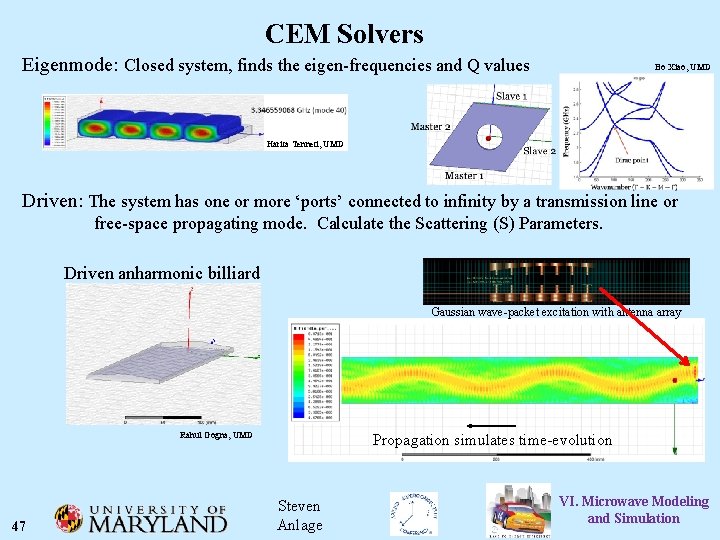
CEM Solvers Eigenmode: Closed system, finds the eigen-frequencies and Q values Bo Xiao, UMD Harita Tenneti, UMD Driven: The system has one or more ‘ports’ connected to infinity by a transmission line or free-space propagating mode. Calculate the Scattering (S) Parameters. Driven anharmonic billiard Gaussian wave-packet excitation with antenna array Rahul Gogna, UMD 47 Propagation simulates time-evolution Steven Anlage VI. Microwave Modeling and Simulation

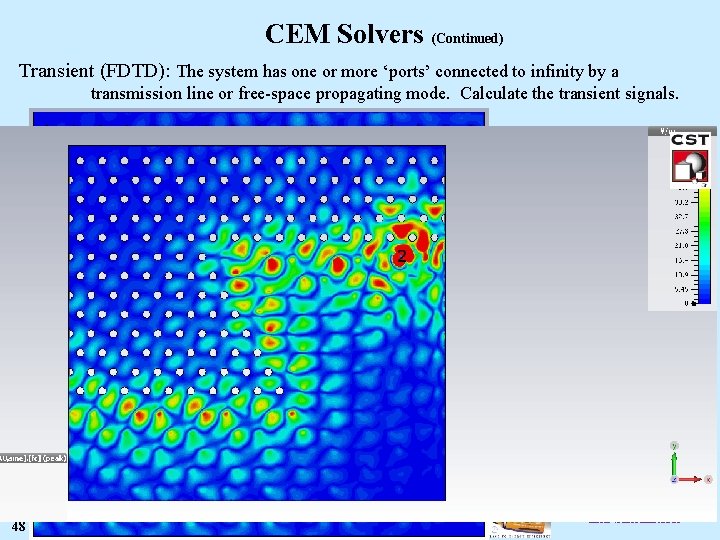
CEM Solvers (Continued) Transient (FDTD): The system has one or more ‘ports’ connected to infinity by a transmission line or free-space propagating mode. Calculate the transient signals. Domain wall Loop antenna (3 turns) Bo Xiao, UMD 48 Steven Anlage VI. Microwave Modeling and Simulation

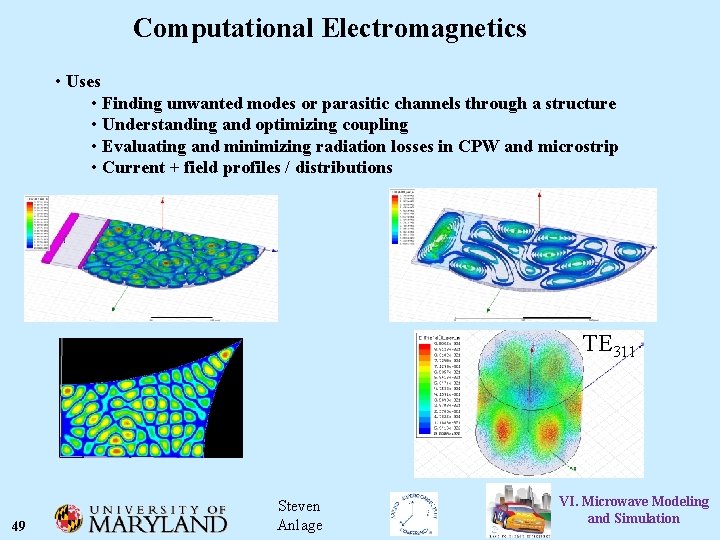
Computational Electromagnetics • Uses • Finding unwanted modes or parasitic channels through a structure • Understanding and optimizing coupling • Evaluating and minimizing radiation losses in CPW and microstrip • Current + field profiles / distributions TE 311 49 Steven Anlage VI. Microwave Modeling and Simulation

VII. QC-Related Microwave Technology • Isolating the Qubit from External Radiation • Filtering • Attenuation / Screening • Cryogenic Microwave Hardware • Passive Devices (attenuator, isolator, circulator, directional coupler) • Active Devices (Amplifiers) • Microwave Calibration 50 Steven Anlage VII. QC-Related Microwave Technology

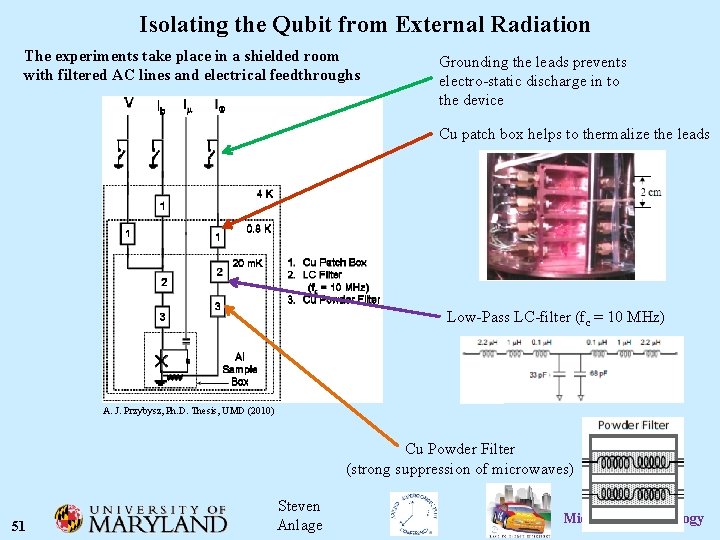
Isolating the Qubit from External Radiation The experiments take place in a shielded room with filtered AC lines and electrical feedthroughs Grounding the leads prevents electro-static discharge in to the device Cu patch box helps to thermalize the leads Low-Pass LC-filter (fc = 10 MHz) A. J. Przybysz, Ph. D. Thesis, UMD (2010) Cu Powder Filter (strong suppression of microwaves) 51 Steven Anlage VII. QC-Related Microwave Technology

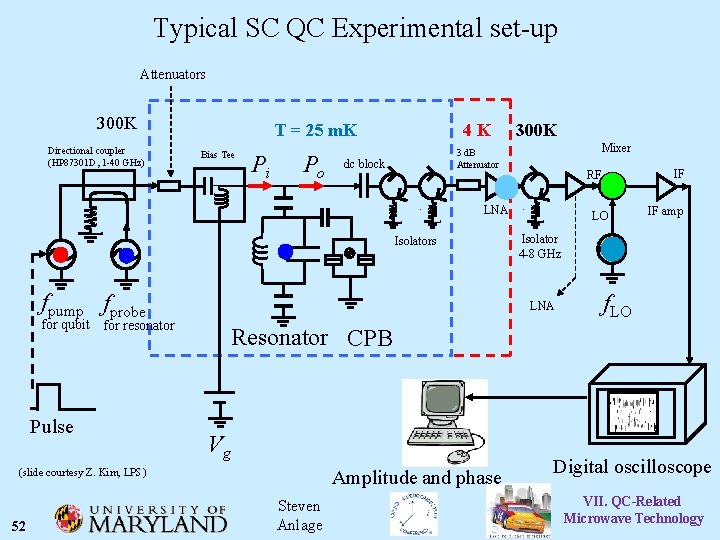
Typical SC QC Experimental set-up Attenuators 300 K Directional coupler (HP 87301 D, 1 -40 GHz) Bias Tee Pi T = 25 m. K 4 K Po 3 d. B Attenuator dc block 300 K Mixer LNA Isolators fpump fprobe Pulse IF amp Isolator 4 -8 GHz f. LO Resonator CPB Vg Amplitude and phase (slide courtesy Z. Kim, LPS) 52 LO LNA for qubit for resonator IF RF Steven Anlage Digital oscilloscope VII. QC-Related Microwave Technology

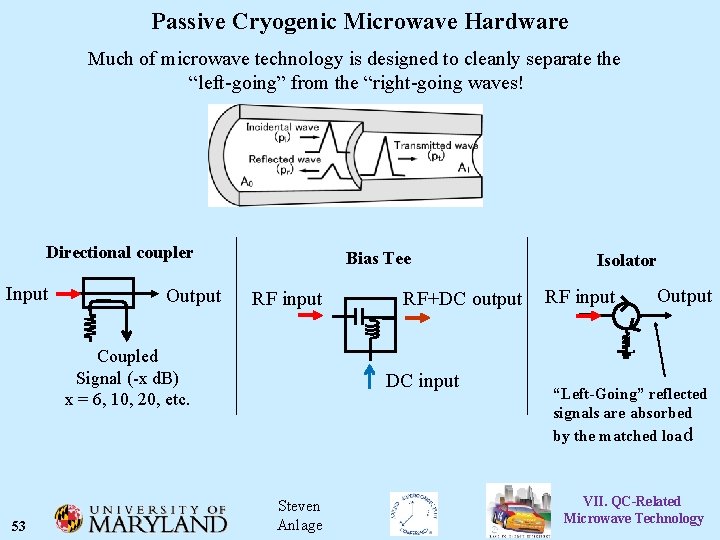
Passive Cryogenic Microwave Hardware Much of microwave technology is designed to cleanly separate the “left-going” from the “right-going waves! Directional coupler Input Output Bias Tee RF input RF+DC output Coupled Signal (-x d. B) x = 6, 10, 20, etc. 53 DC input Steven Anlage Isolator RF input Output “Left-Going” reflected signals are absorbed by the matched load VII. QC-Related Microwave Technology

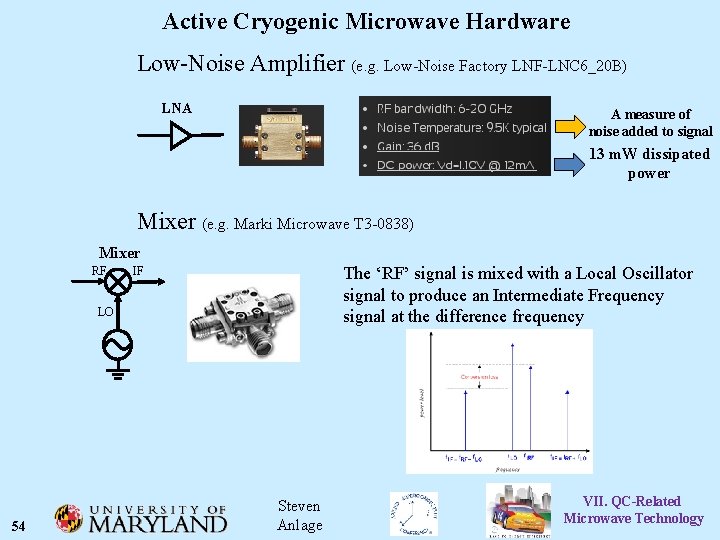
Active Cryogenic Microwave Hardware Low-Noise Amplifier (e. g. Low-Noise Factory LNF-LNC 6_20 B) LNA A measure of noise added to signal 13 m. W dissipated power Mixer (e. g. Marki Microwave T 3 -0838) Mixer RF The ‘RF’ signal is mixed with a Local Oscillator signal to produce an Intermediate Frequency signal at the difference frequency IF LO 54 Steven Anlage VII. QC-Related Microwave Technology

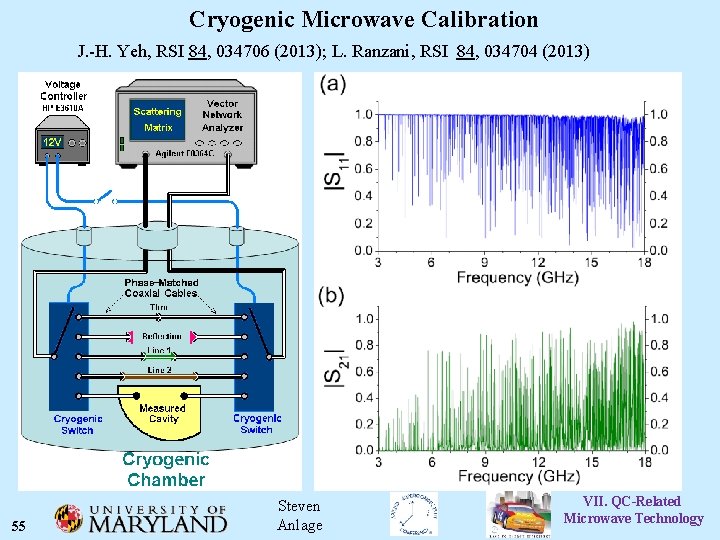
Cryogenic Microwave Calibration J. -H. Yeh, RSI 84, 034706 (2013); L. Ranzani, RSI 84, 034704 (2013) 55 Steven Anlage VII. QC-Related Microwave Technology

References and Further Reading Z. Y. Shen, “High-Temperature Superconducting Microwave Circuits, ” Artech House, Boston, 1994. M. J. Lancaster, “Passive Microwave Device Applications, ” Cambridge University Press, Cambridge, 1997. M. A. Hein, “HTS Thin Films at Microwave Frequencies, ” Springer Tracts of Modern Physics 155, Springer, Berlin, 1999. “Microwave Superconductivity, ” NATO- ASI series, ed. by H. Weinstock and M. Nisenoff, Kluwer, 2001. T. Van. Duzer and C. W. Turner, “Principles of Superconductive Devices and Circuits, ” Elsevier, 1981. T. P. Orlando and K. A. Delin, “Fundamentals of Applied Superconductivity, ” Addison-Wesley, 1991. R. E. Matick, “Transmission Lines for Digital and Communication Networks, ” IEEE Press, 1995; Chapter 6. Alan M. Portis, “Electrodynamcis of High-Temperature Superconductors, ” World Scientific, Singapore, 1993. Steven Anlage 56

Superconductivity Links Wikipedia article on Superconductivity http: //en. wikipedia. org/wiki/Superconductivity Gallery of Abrikosov Vortex Lattices http: //www. fys. uio. no/super/vortex/ Graduate course on Superconductivity (Anlage) http: //www. physics. umd. edu/courses/Phys 798 I/anlage/Anlage. Fall 12/index. html You. Tube videos of Superconductivity (a classic film by Prof. Alfred Leitner) http: //www. youtube. com/watch? v=n. LWUt. UZv. OP 8 57 Steven Anlage

58 Steven Anlage

Please Ask Questions! 59 Steven Anlage

60 Steven Anlage

Details and Backup Slides 61 Steven Anlage

[Return] What are the Limits of Superconductivity? Normal State Phase Diagram Jc Superconducting State Tc Ginzburg-Landau free energy density 62 Temperature Dependence Steven Anlage Currents m 0 Hc 2 Applied Magnetic Field

[Return] BCS Theory of Superconductivity Bardeen-Cooper-Schrieffer (BCS) Cooper Pair s-wave ( = 0) pairing + + S + + v Spin singlet pair v + + S Second electron is attracted to the concentration of positive charges left behind by the first electron First electron polarizes the lattice WDebye is the characteristic phonon (lattice vibration) frequency N(EF) is the electronic density of states at the Fermi Energy V is the attractive electron-electron interaction A many-electron quantum wavefunction Y made up of Cooper pairs is constructed with these properties: An energy 2 D(T) is required to break a Cooper pair into two quasiparticles (roughly speaking) Cooper pair ‘size’: 63 http: //www. chemsoc. org/exemplarchem/entries/igrant/hightctheory_noflash. html Steven Anlage

[Return] s = s 1 -is 2 (p nse 2/m)d(w) Superconductor Electrodynamics T = 0 s 1 ( ) s 2( ) ~ 1/ ideal s-wave Normal State (T > Tc) (Drude Model) s 2 ( ) ns(T) s 1( ) Superfluid density l 2 ~ m/ns ~ 1/wps 2 0 0 w 1/t 0 0 Tc “binding energy” of Cooper pair (100 GHz ~ few THz) Surface Impedance (w > 0) Normal State Superconducting State (w < 2 D) Penetration depth l(0) ~ 20 – 200 nm Finite-temperature: Xs(T) = w. L = wm 0 l(T) → ∞ as T →Tc (and wps(T) → 0) Narrow wire or thin film of thickness t : L(T) = m 0 l(T) coth(t/l(T)) → m 0 l 2(T)/t Kinetic Inductance 64 Steven Anlage T

[Return] BCS Microwave Electrodynamics Low Microwave Dissipation Full energy gap → Rs can be made arbitrarily small for T < Tc/3 in a fully-gapped SC Ds Rs, residual ~ 10 -9 W at 1. 5 GHz in Nb ky Filled Fermi Sea node HTS materials have nodes in Dd the energy gap. This leads to power-law behavior of l(T) and Rs(T) and residual losses kx ky Filled Fermi Sea kx Rs, residual ~ 10 -5 W at 10 GHz in YBa 2 Cu 3 O 7 -d 65 Steven Anlage M. Hein, Wuppertal

[Return] The London Equations t = momentum relaxation time Js = ns e vs Newton’s 2 nd Law for a charge carrier Superconductor: 1/t 0 1 st London Equation 1 st London Eq. and (Faraday) yield: London surmise 2 nd London Equation These equations yield the Meissner screening vacuum superconductor l. L is frequency independent (w < 2 D/ħ) 66 Steven Anlage l. L ~ 20 – 200 nm

[Return] The London Equations continued Normal metal Superconductor E is the source of Jn E=0: Js goes on forever B is the source of zero frequency Js, spontaneous flux exclusion Lenz’s Law 1 st London Equation E is required to maintain an ac current in a SC Cooper pair has finite inertia QPs are accelerated and dissipation occurs 67 Steven Anlage

[Return] Fluxoid Quantization Superconductor is described by a single Macroscopic Quantum Wavefunction Flux F Consequences: Surface S Magnetic flux is quantized in units of F 0 = h/2 e (= 2. 07 x 10 Tm ) R = 0 allows persistent currents Current I flows to maintain F = n F 0 in loop I Circuit C n = integer, h = Planck’s const. , 2 e = Cooper pair charge -15 2 superconductor B Fluxoid Quantization n = 0, ± 1, ± 2, … Flux F 68 Steven Anlage

[Return] Cavity Perturbation Objective: determine Rs, Xs (or s 1, s 2) from f 0 and Q measurements of a resonant cavity containing the sample of interest Input ~ microwavelength l Microwave Resonator Output transmission T 1 T 2 B df df’ Sample at Temperature T f 0 Quality Factor f 0’ frequency Df = f 0’ – f 0 D(Stored Energy) D(1/2 Q) D(Dissipated Energy) Cavity perturbation means Df << f 0 G is the sample/cavity geometry factor 69 Steven Anlage III. Network Analysis

Superconducting Quantum Interference Devices (SQUIDs) [Return] The DC SQUID A Sensitive Magnetic Flux-to-Voltage Transducer Bias Current Ic Flux 2 Ic Ic Wikipedia. org One can measure small fields (e. g. 5 a. T) with low noise (e. g. 3 f. T/Hz 1/2) Used extensively for Magnetometry (m vs. H) Magnetoencephalography (MEG) Magnetic microscopy Low-field magnetic resonance imaging 70 Steven Anlage

Superconducting Quantum Interference Devices (SQUIDs) [Return] The RF SQUID A High-Frequency Magnetic Flux-to-Voltage Transducer RF SQUID Tank Circuit R. Rifkin, J. Appl. Phys. (1976) Not as sensitive as DC SQUIDs Less susceptible to noise at 77 K with HTS junctions Basis for many qubit and meta-atom designs 71 Steven Anlage

[Return] Transmission Lines, continued The power absorbed in a termination is: Model of a realistic transmission line including loss Shunt Conductance Traveling Wave solutions 72 with Steven Anlage III. Network Analysis

[Return] How Much Power Reaches the Load? Agilent – Back to Basics Seminar 73 Steven Anlage III. Network Analysis

Waveguides [Return] H Rectangular metallic waveguide 74 Steven Anlage III. Network Analysis

Transmission Line Resonators [Return] Transmission Line Model Transmission Line Unit Cell Transmission Line Resonator Model Ccoupling 75 Ccoupling Steven Anlage IV. Superconducting Microwave Resonators for QC

[Return] Measuring the Q of a Shunt-Coupled Resonator Ch. Kaiser, Sup Sci Tech 23, 075008 (2010) 76 Steven Anlage

[Return] Rapid Single Flux Quantum Logic superconducting “classical” digital computing Ibias ~1 m. V Input JJ ~2 ps Ø When (Input + Ibias) exceeds JJ critical current Ic, JJ “flips”, producing an SFQ pulse. Ø Area of the pulse is F 0=2. 067 m. V-ps Ø Pulse width shrinks as JC increases Ø SFQ logic is based on counting single flux quanta Courtesy Arnold Silver 77 Steven Anlage Ø SFQ pulses propagate along impedance-matched passive transmission line (PTL) at the speed of light in the line (~ c/3). Ø Multiple pulses can propagate in PTL simultaneously in both directions. Circuits can operate at 100’s of GHz Ø

[Return] Mesoscopic Superconductivity BCS Ground state wavefunction Coherent state with no fixed number of Cooper pairs Number-phase uncertainty (conjugate variables) Typically: Rbarrier > 2ħ/e 2 ~ 6 k. W Bulk Superconductor Small superconducting island e 2/2 C > k. BT (requires C ~ f. F at 1 K) Classical energy Josephson tunnel barrier phase difference g Using Q = CV and Q/2 e = N = i ∂/∂f = i ∂/∂g the Hamiltonian is: KE Two important limits: EC << EJ well-define phase f utilize phase eigenstates, like EC >> EJ all values of f equally probable utilize number eigenstates 78 Steven Anlage PE