Basics of Phases and Phase Transformations W Pschl

Basics of Phases and Phase Transformations W. Püschl University of Vienna

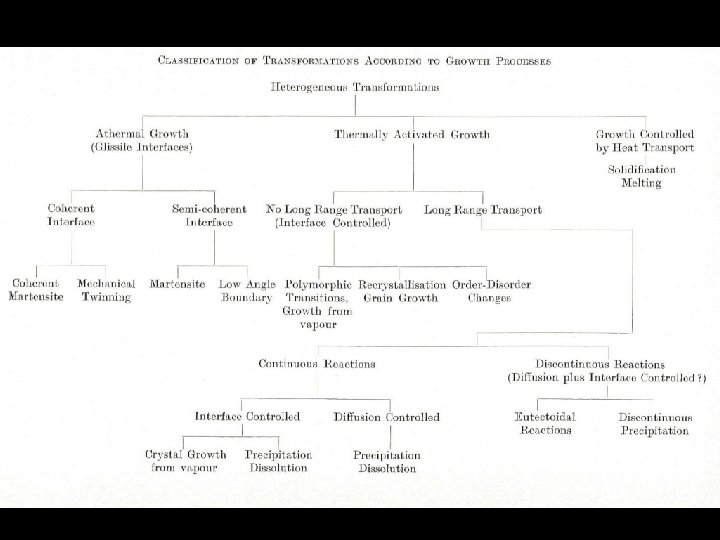
Content 1. Historical context 2. Classification of phase transformations 3. Graphical thermodynamics – Phase diagrams 4. Miscibility Gap – Precipitation nucleation vs. spinodal decomposition 5. Order 6. Ising model: atomic and magnetic spin configuration 7. Martensitic transformations

Early technological application of poly-phase systems: Damascus Steel
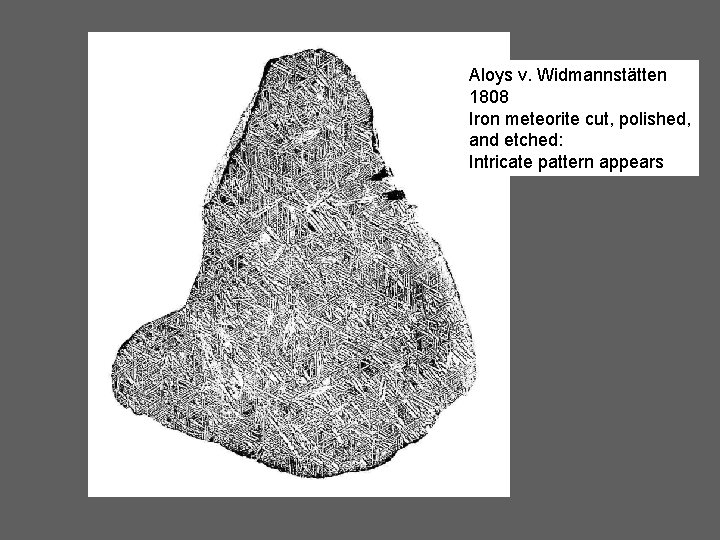
Aloys v. Widmannstätten 1808 Iron meteorite cut, polished, and etched: Intricate pattern appears
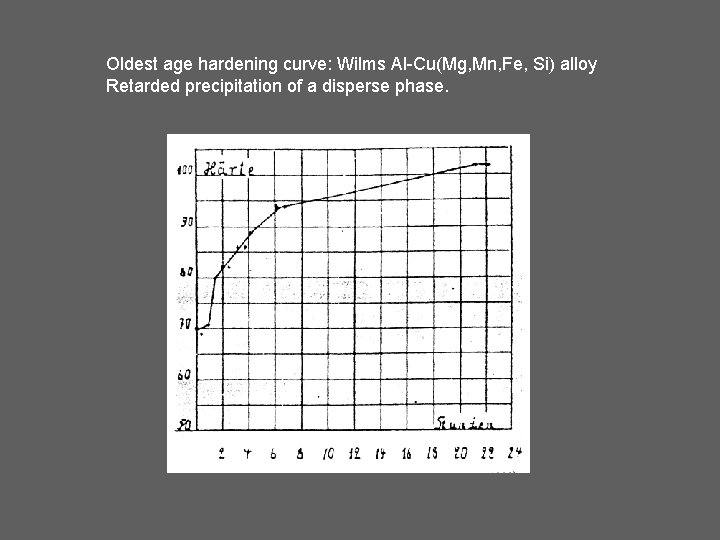
Oldest age hardening curve: Wilms Al-Cu(Mg, Mn, Fe, Si) alloy Retarded precipitation of a disperse phase.

A scientific understanding of phases and phase transformation begins to develop end 19 th / beginning 20 th centuries physical metallurgy Experimental: Gustav Tammann (Göttingen) Theoretical: Josiah Willard Gibbs

What is a phase? Region where intrinsic parameters have (more or less) the same value lattice structure, composition x, degree of order , density , … Need not be simply (singly) connected. Expreme example: disperse phase and matrix phase where it is embedded (like Swiss cheese) When is a phase thermodynamically stable? How can we determine wihich phase is stable at a certain composition, temperature (and pressure, magnetic field…) What happens if this is not the case metastability or phase transition How can a phase transition take place?
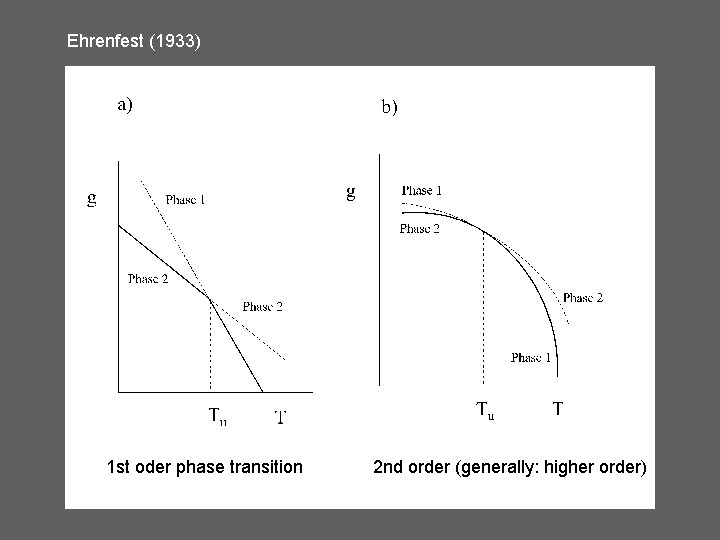
Ehrenfest (1933) 1 st oder phase transition 2 nd order (generally: higher order)
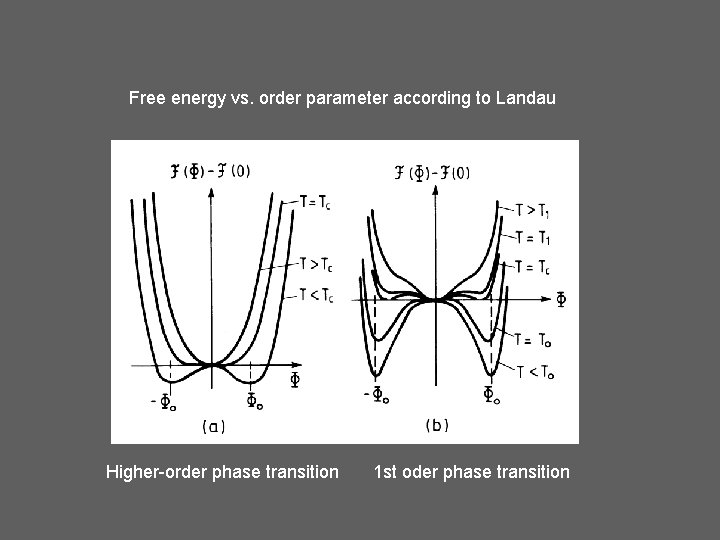
Free energy vs. order parameter according to Landau Higher-order phase transition 1 st oder phase transition
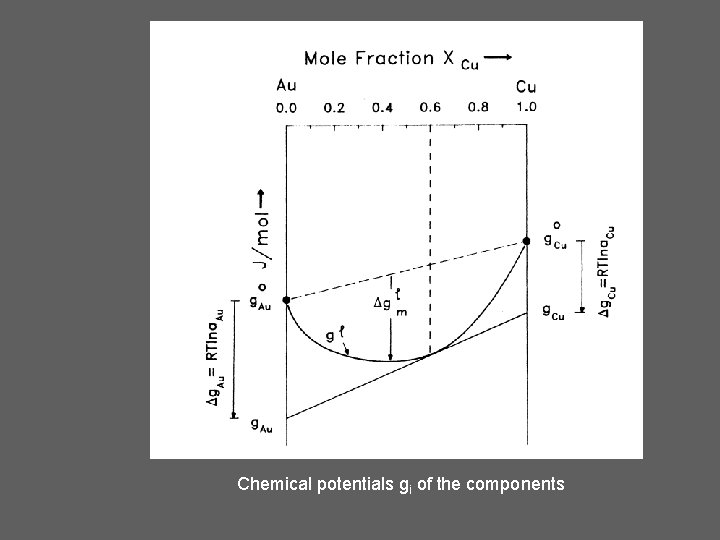
Chemical potentials gi of the components
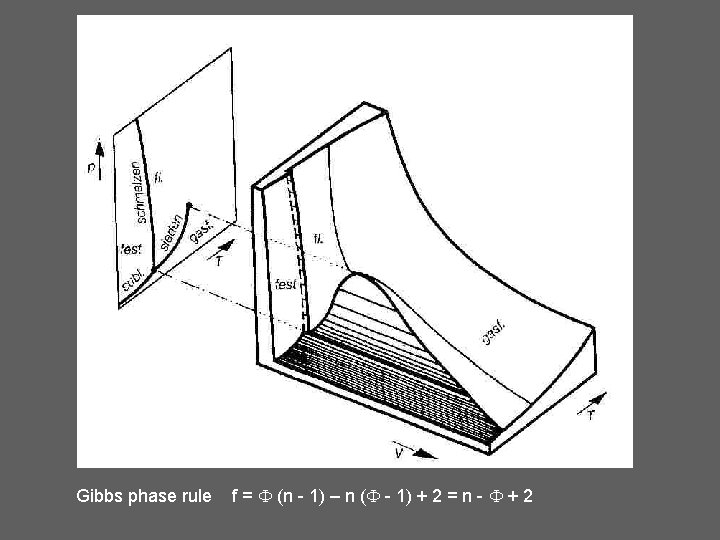
Gibbs phase rule f = (n - 1) – n ( - 1) + 2 = n - + 2
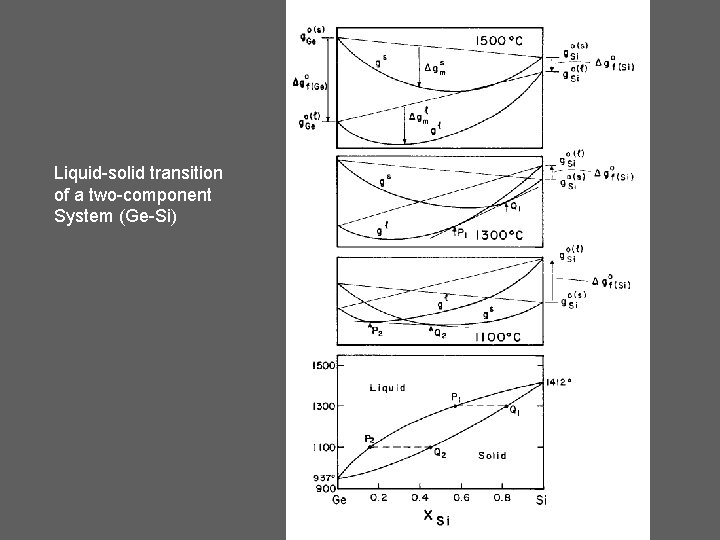
Liquid-solid transition of a two-component System (Ge-Si)

Excess enthalpy and miscibility gap
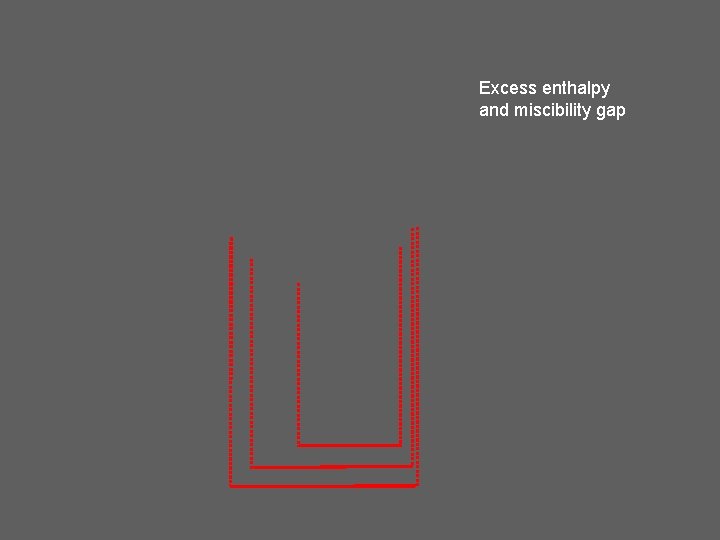
Excess enthalpy and miscibility gap

Precipitation: alternative mechanisms

Heterophase fluctuation corresponds to nucleation Homophase fluctuation corresponds to spinodal decomposition
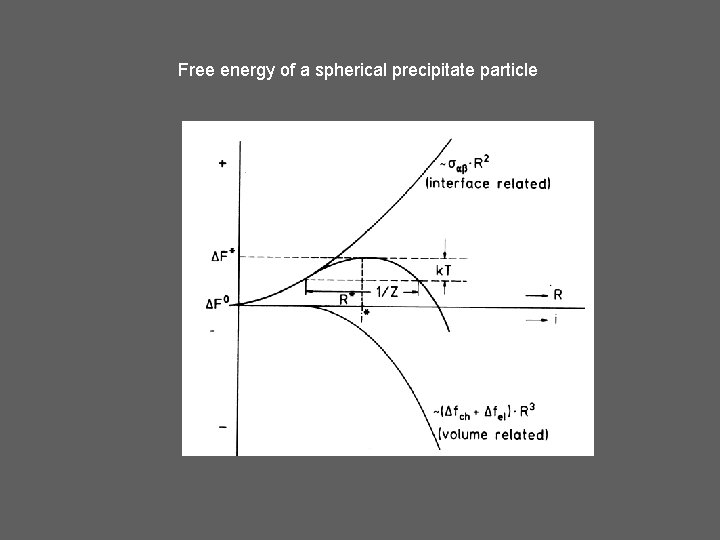
Free energy of a spherical precipitate particle

Precipitation by nucleation and growth: NV particle number, c supersaturation, mean particle radius Ni 36 Cu 9 Al 55

Spinodal Decomposition
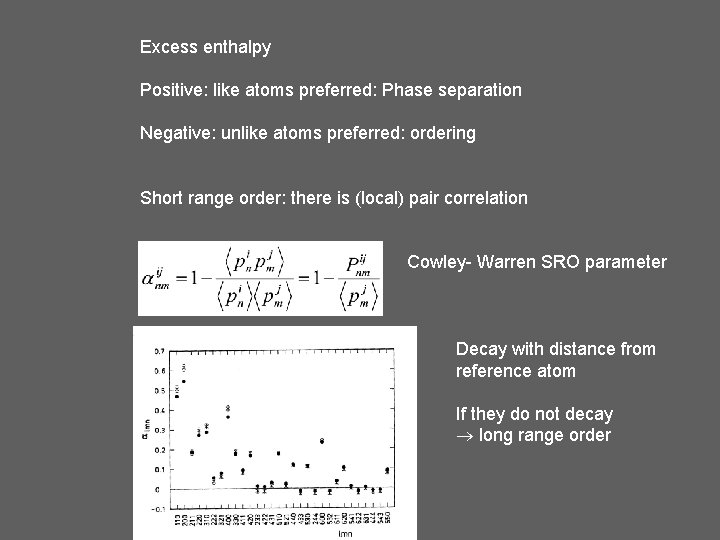
Excess enthalpy Positive: like atoms preferred: Phase separation Negative: unlike atoms preferred: ordering Short range order: there is (local) pair correlation Cowley- Warren SRO parameter Decay with distance from reference atom If they do not decay long range order
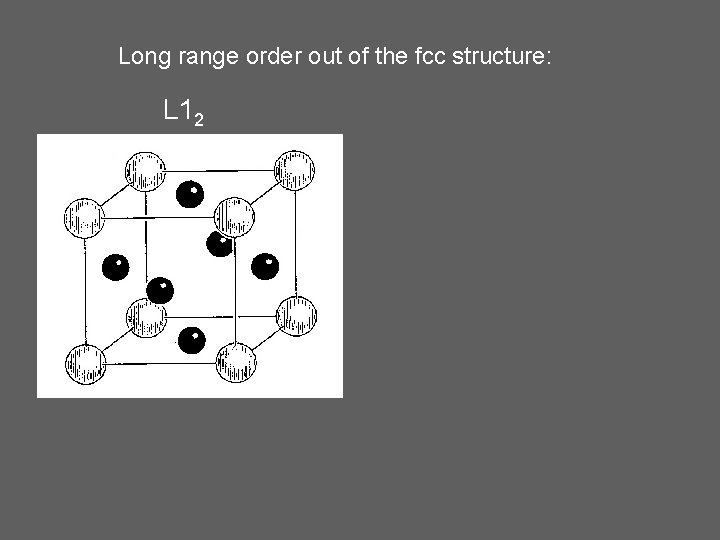
Long range order out of the fcc structure: L 12
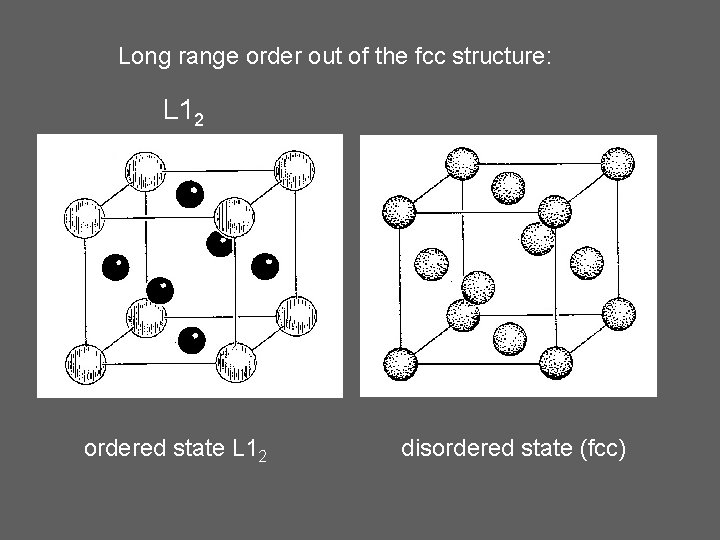
Long range order out of the fcc structure: L 12 ordered state L 12 disordered state (fcc)
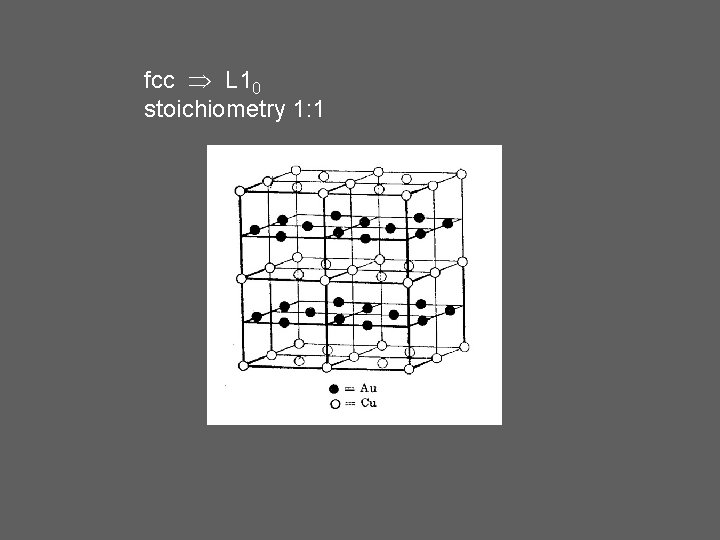
fcc L 10 stoichiometry 1: 1

Different long range ordered structures in the Cu-Au phase diagram L 12 L 10
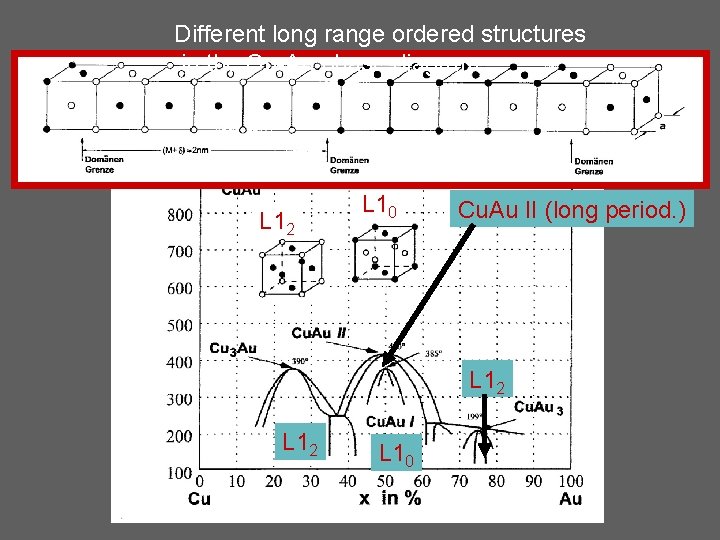
Different long range ordered structures in the Cu-Au phase diagram L 12 L 10 Cu. Au II (long period. ) L 12 L 10

Statistical physics of ordered alloys Partition function Possibly different vibration spectrum for every atom configuration Does it really matter?
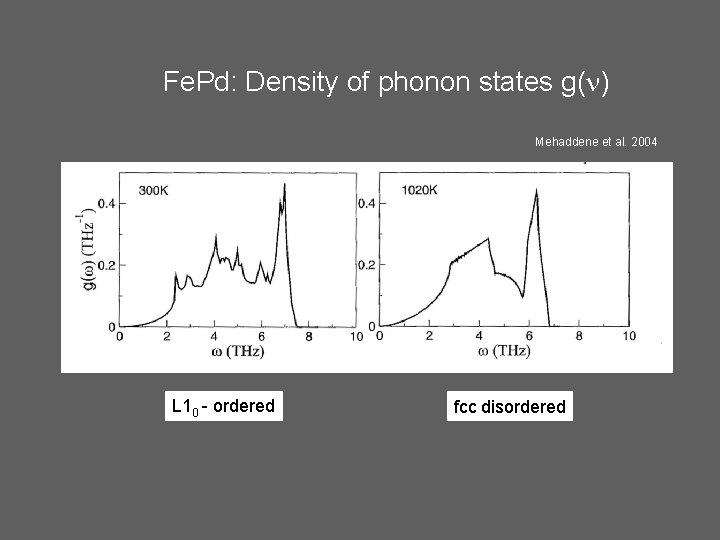
Fe. Pd: Density of phonon states g( ) Mehaddene et al. 2004 L 10 - ordered fcc disordered
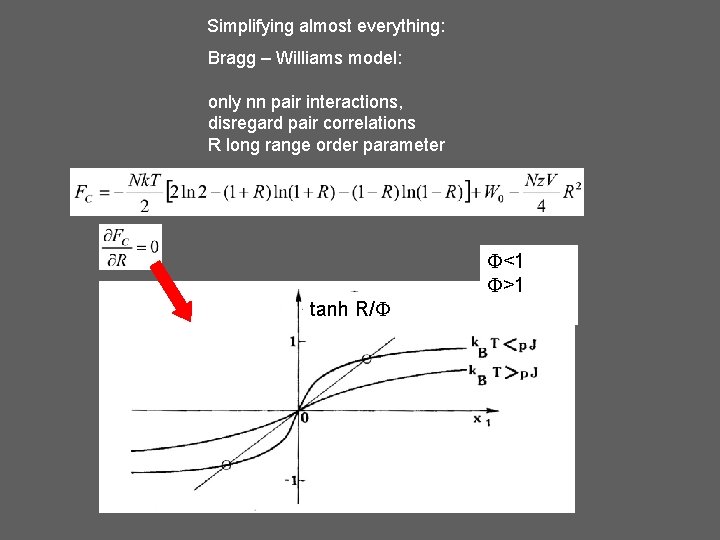
Simplifying almost everything: Bragg – Williams model: only nn pair interactions, disregard pair correlations R long range order parameter <1 >1 tanh R/
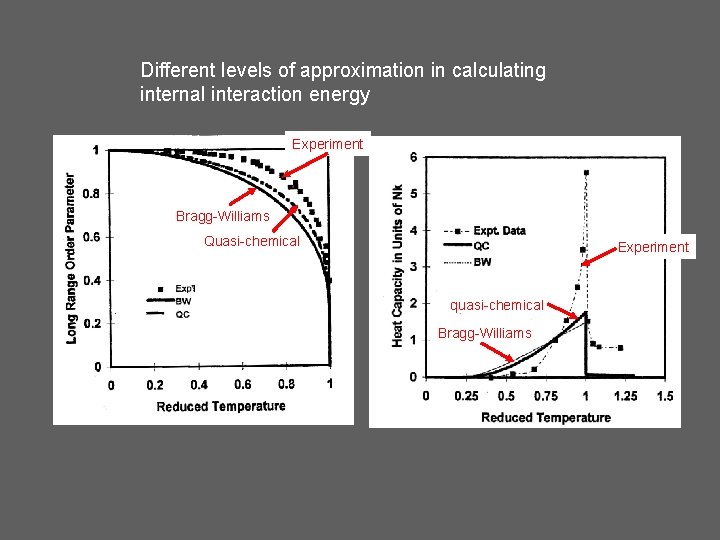
Different levels of approximation in calculating internal interaction energy Experiment Bragg-Williams Quasi-chemical Experiment quasi-chemical Bragg-Williams
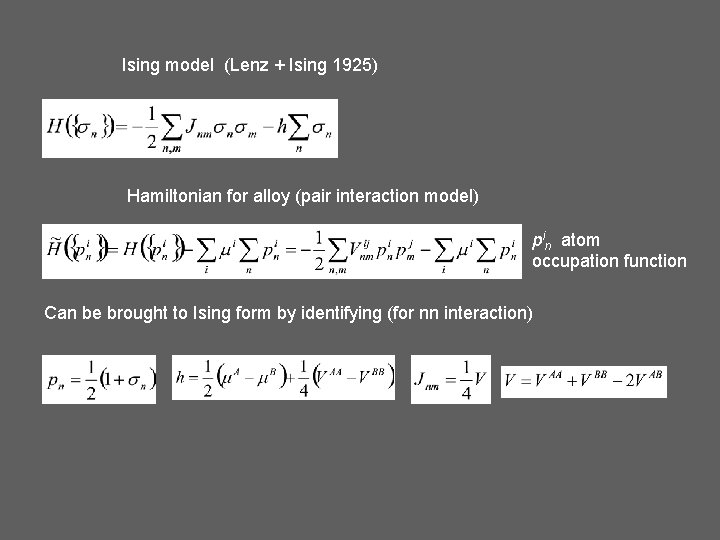
Ising model (Lenz + Ising 1925) Hamiltonian for alloy (pair interaction model) pin atom occupation function Can be brought to Ising form by identifying (for nn interaction)

Idea of mean field model: treat a few local interactions explicitly, environment of similar cells is averaged and exerts a mean field of interaction

Local interaction only 1 atom Bragg- Williams – model Correspondences: Phase-separating ----- ferromagnetic Long range ordering ----- antiferromagnetic

Structure on polished surface after martensitic transformation: roof-like, but no steps. A scratched line remains continuous

Martensite morphologies
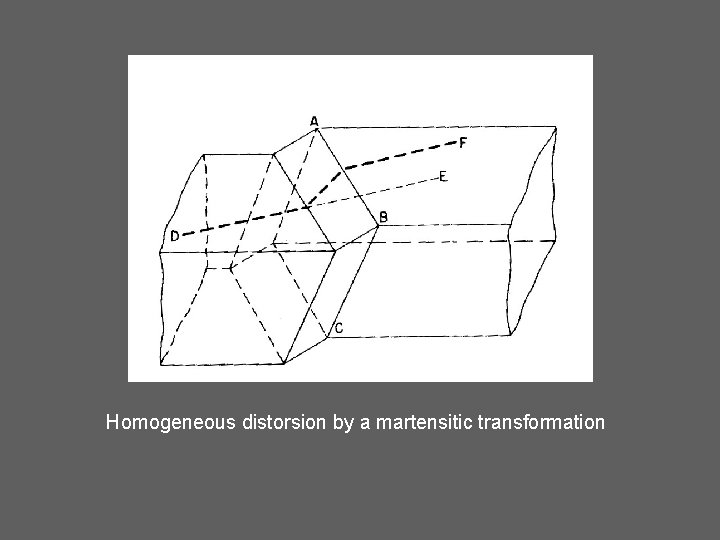
Homogeneous distorsion by a martensitic transformation
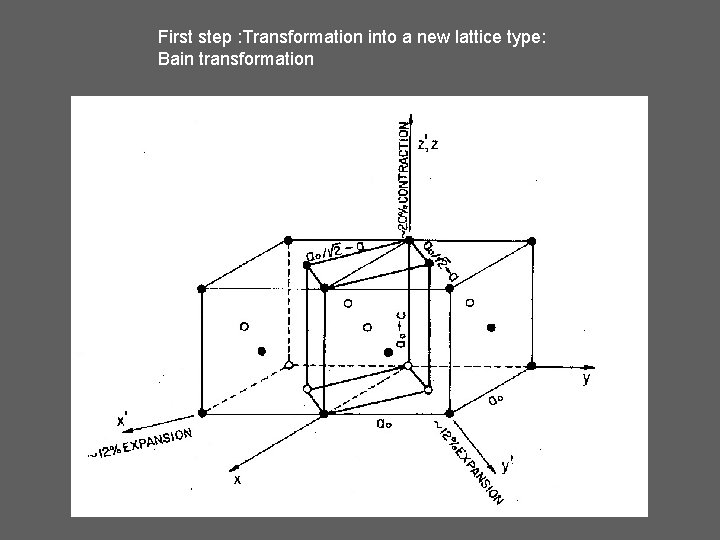
First step : Transformation into a new lattice type: Bain transformation
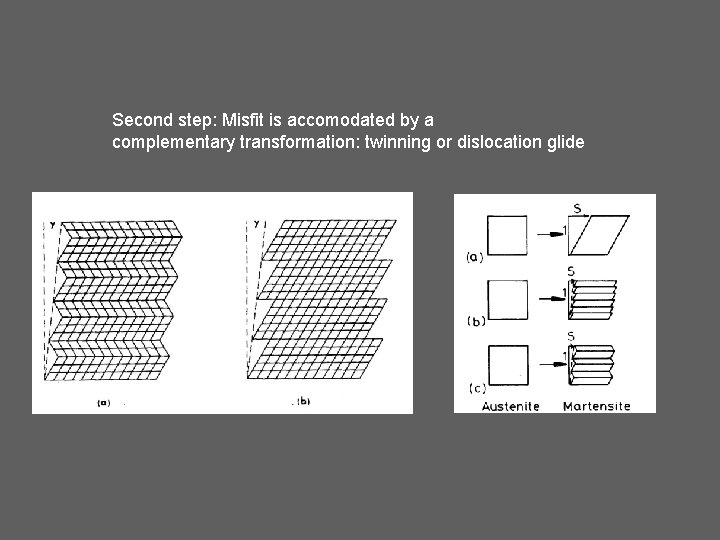
Second step: Misfit is accomodated by a complementary transformation: twinning or dislocation glide

Thermoelastic Martensites: Four symmetric variants per glide plane: Can be transformed into one another by twinning
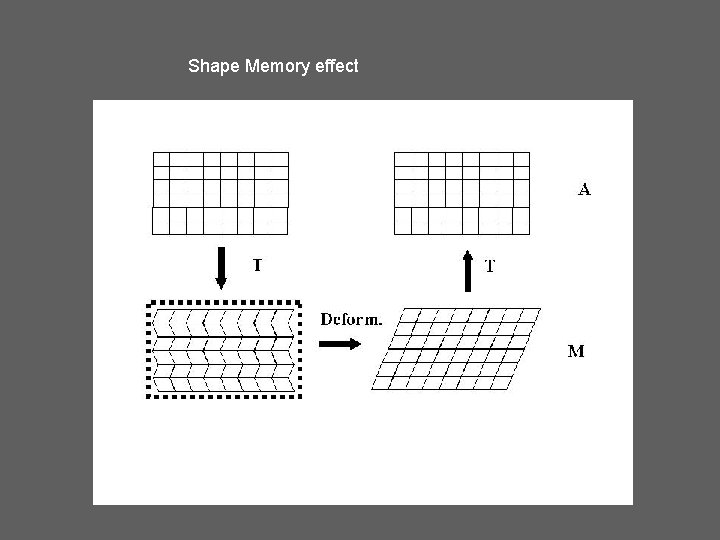
Shape Memory effect

Final remarks: As the number of components grows and interaction mechanisma are added, phase transformations can gain considerable complexity For instance: Phase separation and ordering (opposites in simple systems) may happen at the same time. I have completely omitted many interesting topics, for instance Gas-to-liquid or liquid-to-liquid transformations The role of quantum phenomena at low-temperature phases Dynamical phase transformations, self-organized phases far from equilibrium
- Slides: 41