Basics of ML Theory Example Classifying Tasty Apples

Basics of ML Theory

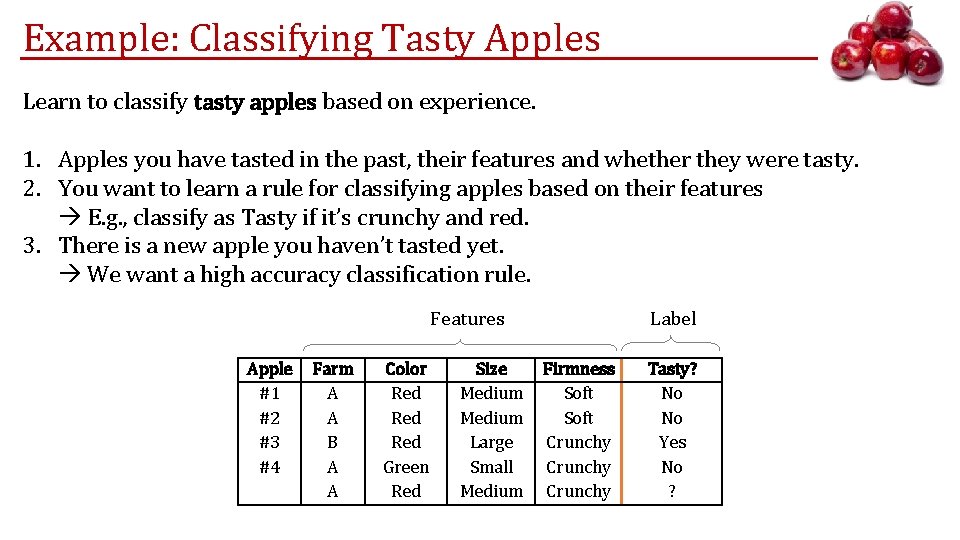
Example: Classifying Tasty Apples Learn to classify tasty apples based on experience. 1. Apples you have tasted in the past, their features and whether they were tasty. 2. You want to learn a rule for classifying apples based on their features E. g. , classify as Tasty if it’s crunchy and red. 3. There is a new apple you haven’t tasted yet. We want a high accuracy classification rule. Label Features Apple #1 #2 #3 #4 Farm A A B A A Color Red Red Green Red Size Medium Large Small Medium Firmness Soft Crunchy Tasty? No No Yes No ?

Framework for Offline Learning Informal Goal of classification

On the possibility of learning •

On the possibility of learning • 0 1

Uniform Convergence, Beyond Classification • E. g. , revenue function, welfare, etc.

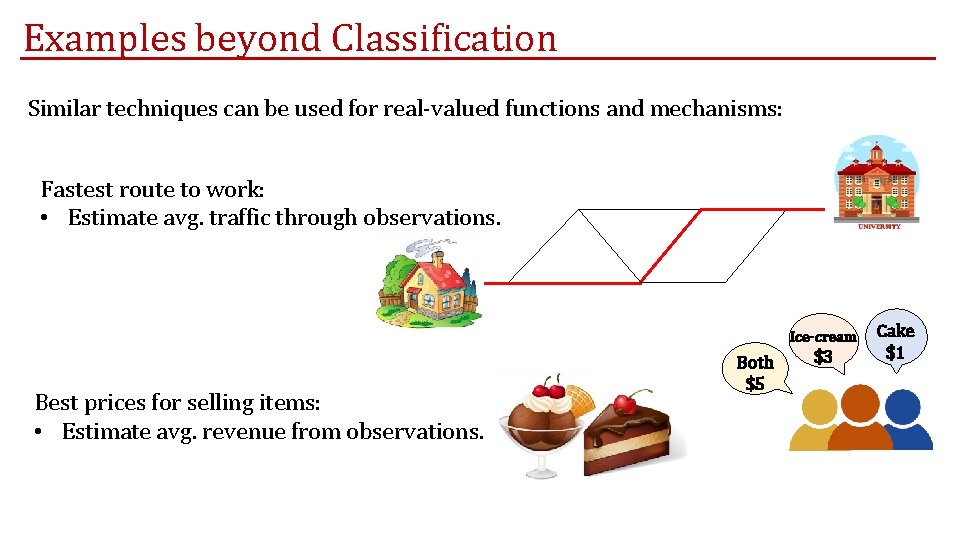
Examples beyond Classification Similar techniques can be used for real-valued functions and mechanisms: Fastest route to work: • Estimate avg. traffic through observations. Ice-cream Best prices for selling items: • Estimate avg. revenue from observations. Both $5 $3 Cake $1

Mechanism Design as Offline Learning • Mechanism Design as Learning

Online Learning Model In machine learning, the data might not be coming from a distribution: • The environment is evolving over time in an unpredictable way. • We don’t want to make any assumptions on how the data evolves. • We want to make decisions on any instance as soon as it arrives. Traffic fluctuates constructions, pot holes, holidays, etc. Willingness to pay fluctuates holidays, pandemics, …

Online Learning Model In machine learning, the data might not be coming from a distribution: • The environment is evolving over time in an unpredictable way. • We don’t want to make any assumptions on how the data evolves. • We want to make decisions on any instance as soon as it arrives. Online Learning framework

Online Learning Model In machine learning, the data might not be coming from a distribution: • The environment is evolving over time in an unpredictable way. • We don’t want to make any assumptions on how the data evolves. • We want to make decisions on any instance as soon as it arrives. Online Learning in Mechanism Design

1 st Attempt: Repeated Empirical Risk Minimization •

Follow the Perturbed Leader • Theorem: Regret of Follow the Perturbed Leader

Another Good Approach • Multiplicative Weight Update (Hedge) Theorem: Regret of Multiplicative Weight Update

Why does this work?

Partial Information • Partial information: Seeing the traffic on the path we took. Seeing the payment, but not the willingness to pay.

Ideas to deal with Partial Information • Exploration Exploitation

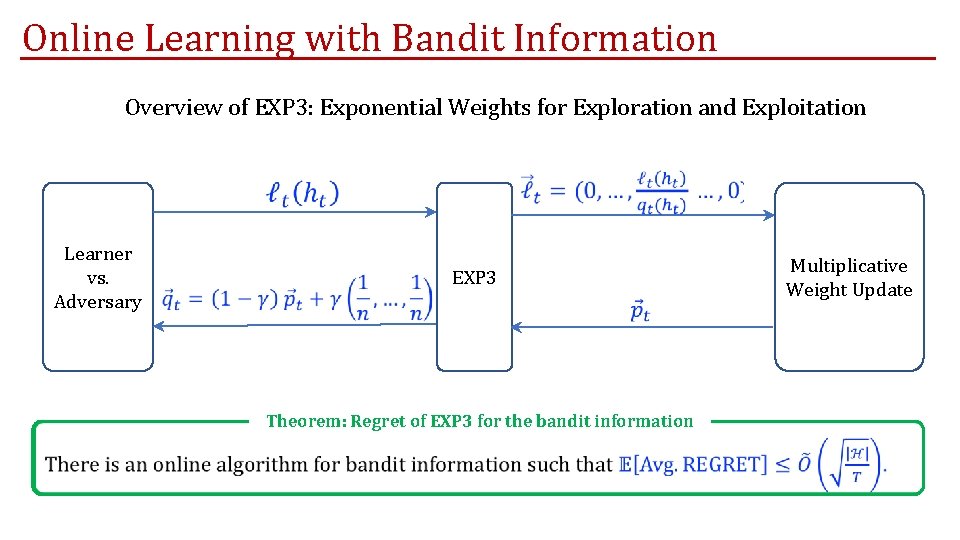
Online Learning with Bandit Information Overview of EXP 3: Exponential Weights for Exploration and Exploitation Learner vs. Adversary EXP 3 Theorem: Regret of EXP 3 for the bandit information Multiplicative Weight Update

Brief Overview of what learned •

Online Learning in Incentive-Compatible Mechanisms

Revenue Maximization in Auctions Ice-cream Both $5 $3 Cake $1 Determine allocation and Payments? Revenue Maximizing Auctions: Myerson’ 81, Cremer & Mc. Lean’ 85, Armstrong’ 00, Ronen’ 01, Balcan et al. ‘ 08, Dobzinski et al’ 11, Papadimitriou & Pierrakos’ 13, Roughgarden & Talgram-Cohen’ 13, Fu et al. ’ 14, Morgenstern & Roughgarden 15 -16, Devanur et al. ’ 16, Balcan et al. ’ 16 -19, …

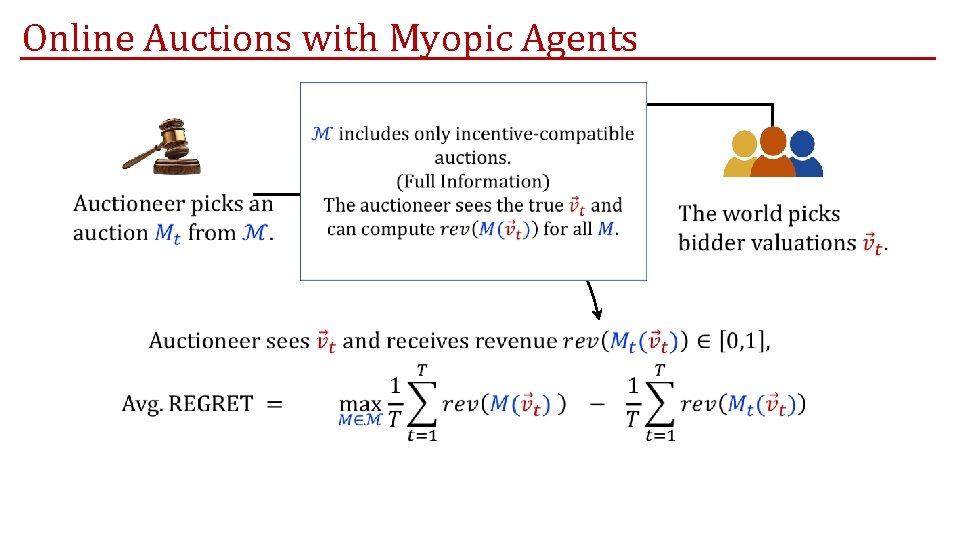
Online Auctions with Myopic Agents

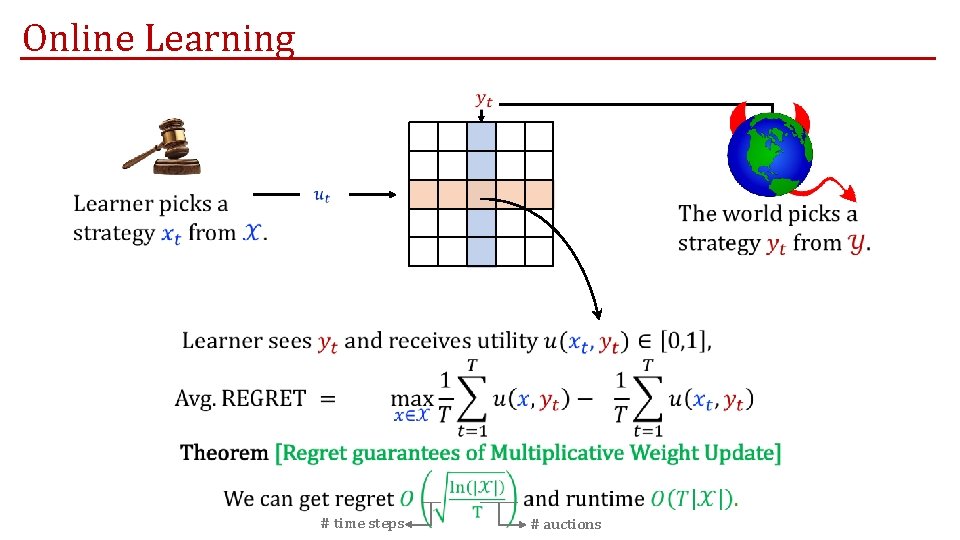
Online Learning # time steps # auctions

Difficulty of Online Optimization in Auctions Effective tools for computing optimal auctions for a distribution over valuations: Compete with the best auction on changing valuations. Oracle-efficient Online Learning

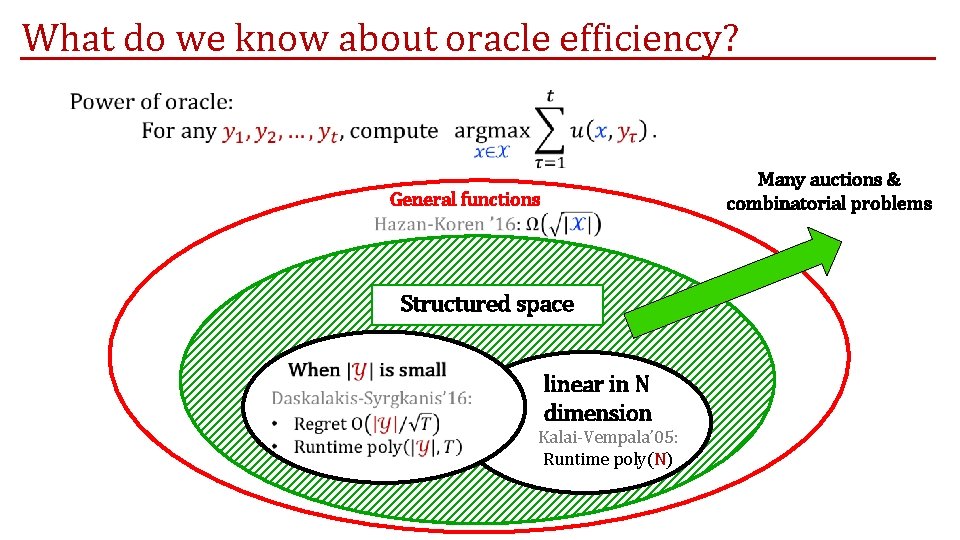
What do we know about oracle efficiency? Many auctions & combinatorial problems General functions Structured space linear in N dimension Kalai-Vempala’ 05: Runtime poly(N)

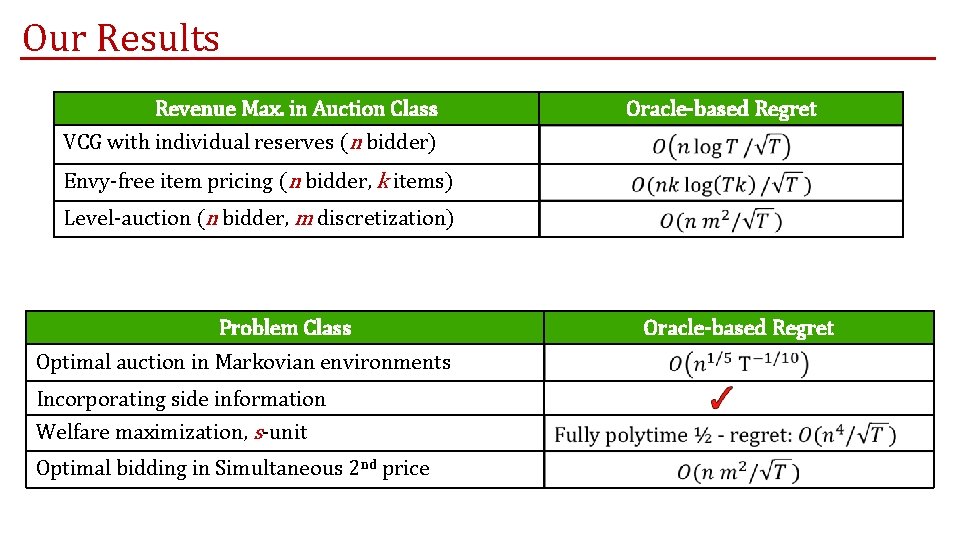
Our Results Revenue Max. in Auction Class Oracle-based Regret VCG with individual reserves (n bidder) Envy-free item pricing (n bidder, k items) Level-auction (n bidder, m discretization) Problem Class Optimal auction in Markovian environments Incorporating side information Welfare maximization, s-unit Optimal bidding in Simultaneous 2 nd price Oracle-based Regret

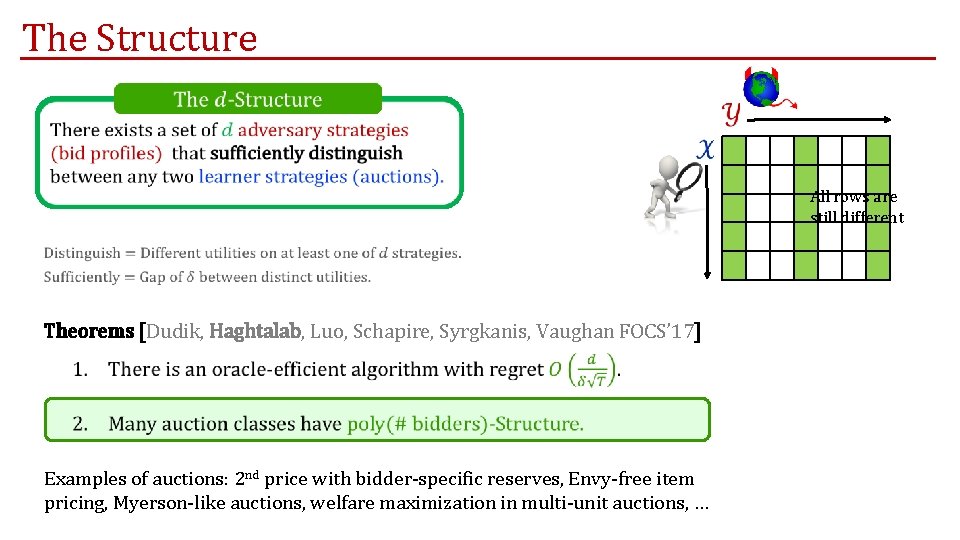
The Structure All rows are still different Theorems [Dudik, Haghtalab, Luo, Schapire, Syrgkanis, Vaughan FOCS’ 17] Examples of auctions: 2 nd price with bidder-specific reserves, Envy-free item pricing, Myerson-like auctions, welfare maximization in multi-unit auctions, …

Structure in 2 nd Price with Individual Reserves

Structure in Auctions Generally For many N-bidder auction classes In many auctions, outcome depends on a few parameters, e. g. , winners, second place in line to winning, and their bid. Auction 1 Winner in Auction 1 Next in line in Auction 1 Auction 2 Next in line in Auction 2 Winner in Auction 2 Bid profiles with 4 non-zero bids distinguish between any two such auction.

Our Algorithm Theorem [Dudik, Haghtalab, Luo, Schapire, Syrgkanis, Vaughan FOCS’ 17] Algorithm: Each round, use history + random fake history: History Fake history All rows are still different Oracle-efficient Historical utility Random Perturbation No Regret?

Our Algorithm Theorem [Dudik, Haghtalab, Luo, Schapire, Syrgkanis, Vaughan FOCS’ 17] Algorithm: Follow-the. Perturbed-Leader Kalai-Vempala’ 05 : Main Ideas Independent Perturb. Some randomness Stability:

Analyzing Stability is small? Groups of equal values Union bound Perturbed utility Not significant

Main Message In many incentive-compatible auctions, computing online optimal auctions on changing preferences comes for free. No need for new optimization tools! Just use empirical risk minimization differently.

Role of Incentive Compatibility and Myopia