Basic Trigonometric Identities and Equations PreCalculus Teacher Mrs

Basic Trigonometric Identities and Equations Pre-Calculus Teacher – Mrs. Volynskaya
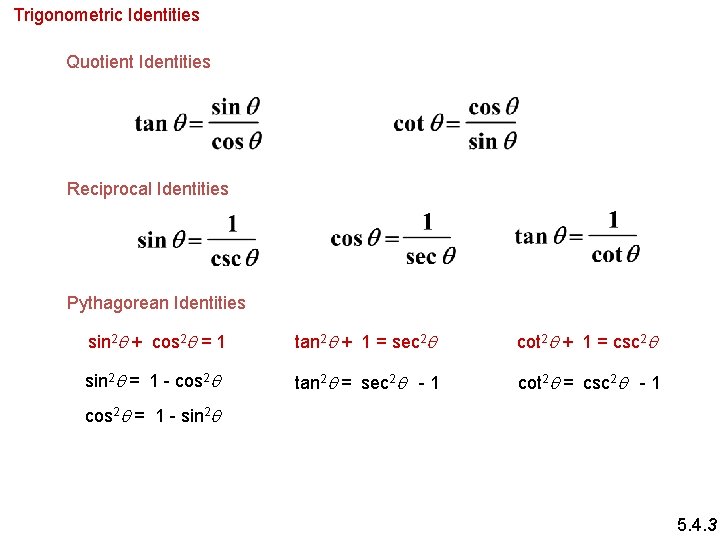
Trigonometric Identities Quotient Identities Reciprocal Identities Pythagorean Identities sin 2 q + cos 2 q = 1 tan 2 q + 1 = sec 2 q cot 2 q + 1 = csc 2 q sin 2 q = 1 - cos 2 q tan 2 q = sec 2 q - 1 cot 2 q = csc 2 q - 1 cos 2 q = 1 - sin 2 q 5. 4. 3

Where did our pythagorean identities come from? ? Do you remember the Unit Circle? • What is the equation for the unit circle? x 2 + y 2 = 1 • What does x = ? What does y = ? (in terms of trig functions) sin 2θ + cos 2θ = 1 Pythagorean Identity!
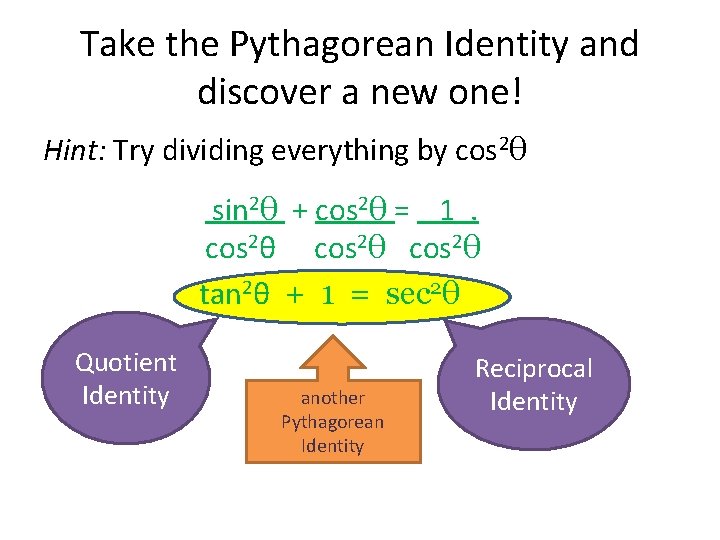
Take the Pythagorean Identity and discover a new one! Hint: Try dividing everything by cos 2θ sin 2θ + cos 2θ = 1. cos 2θ tan 2θ + 1 = sec 2θ Quotient Identity another Pythagorean Identity Reciprocal Identity
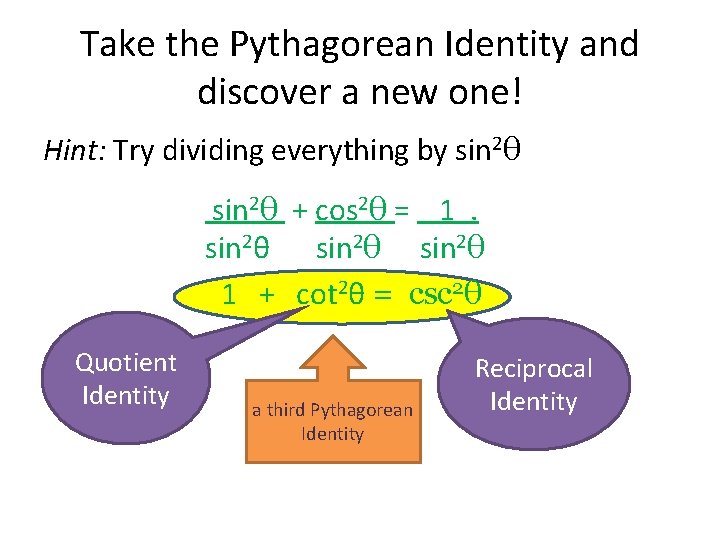
Take the Pythagorean Identity and discover a new one! Hint: Try dividing everything by sin 2θ + cos 2θ = 1. sin 2θ 1 + cot 2θ = csc 2θ Quotient Identity a third Pythagorean Identity Reciprocal Identity

Using the identities you now know, find the trig value. 1. ) If cosθ = 3/4, find secθ 2. ) If cosθ = 3/5, find cscθ.

3. ) sinθ = -1/3, find tanθ 4. ) secθ = -7/5, find sinθ

Simplifying Trigonometric Expressions Identities can be used to simplify trigonometric expressions. Simplify. a) b) 5. 4. 5
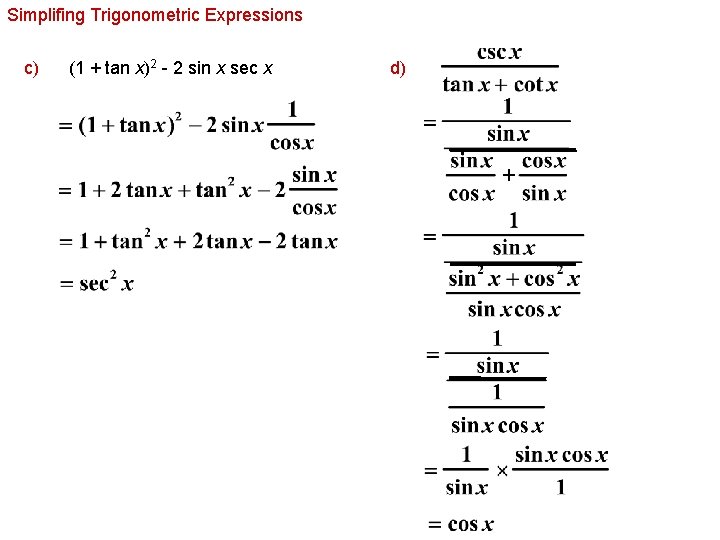
Simplifing Trigonometric Expressions c) (1 + tan x)2 - 2 sin x sec x d)

Simplify each expression.
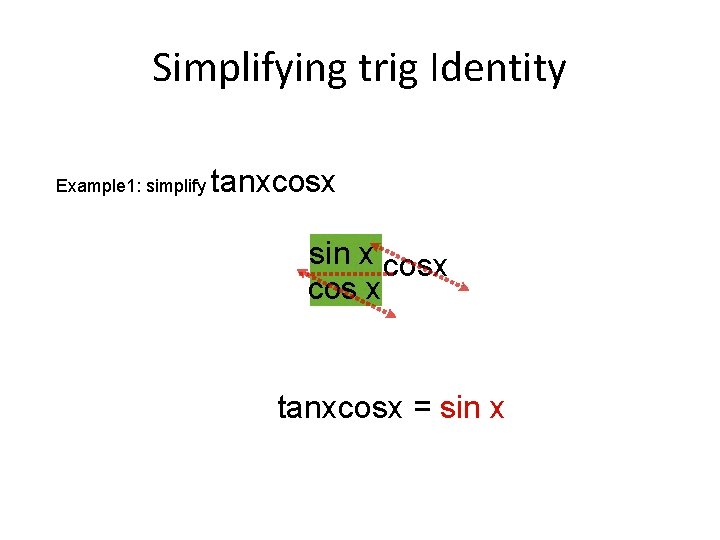
Simplifying trig Identity Example 1: simplify tanxcosx sin x tanx cos x tanxcosx = sin x
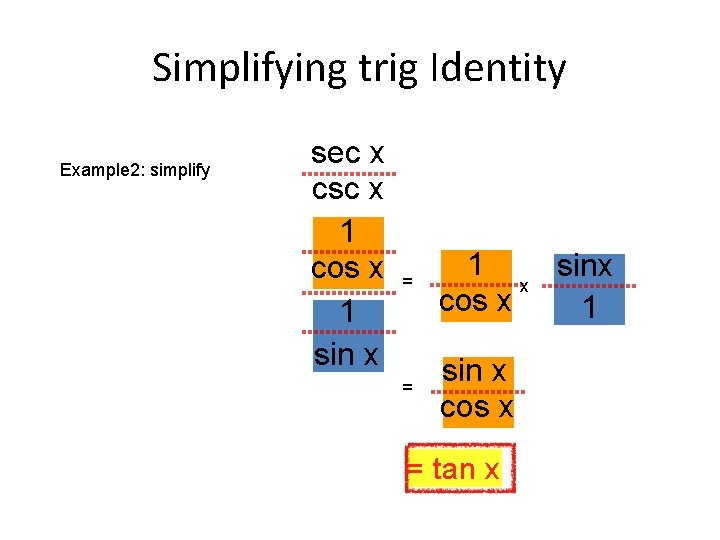
Simplifying trig Identity Example 2: simplify sec x csc x 1 cos sec x csc 1 x sin x = 1 sinx x cos x 1 = sin x cos x = tan x

Simplifying trig Identity Example 2: simplify cos 2 x - sin 2 x cos 2 x - sin 12 x cos x = sec x
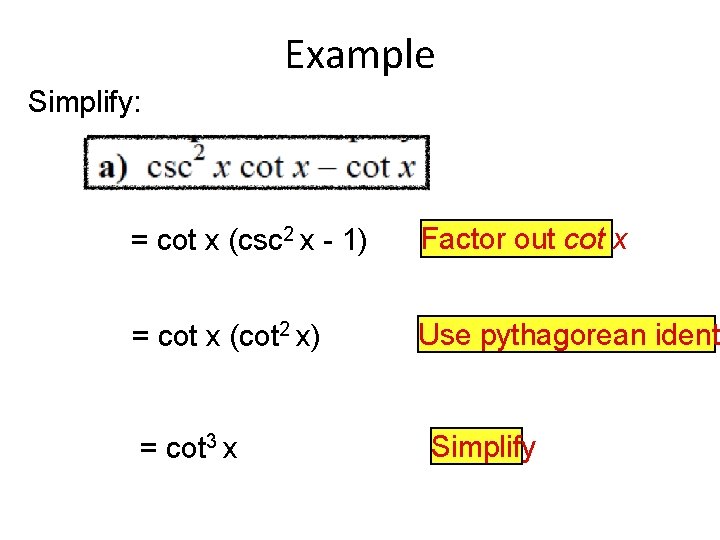
Example Simplify: = cot x (csc 2 x - 1) Factor out cot x = cot x (cot 2 x) Use pythagorean identi = cot 3 x Simplify
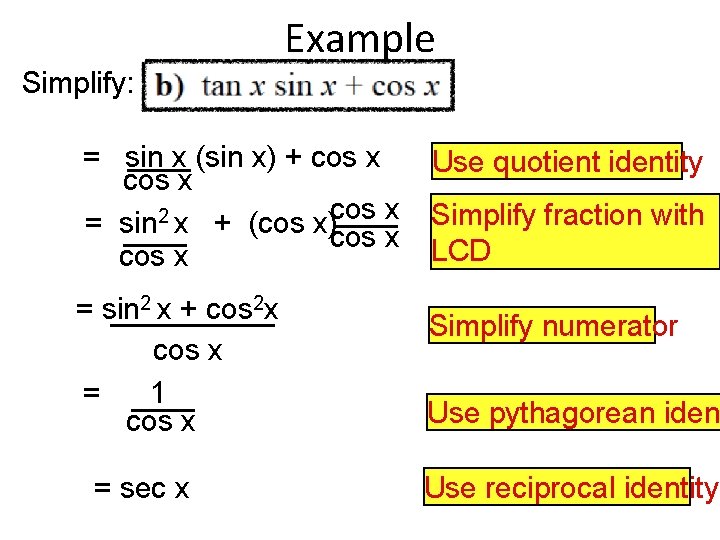
Example Simplify: = sin x (sin x) + cos x 2 = sin x + (cos x)cos x = sin 2 x + cos 2 x cos x = 1 cos x = sec x Use quotient identity Simplify fraction with LCD Simplify numerator Use pythagorean iden Use reciprocal identity
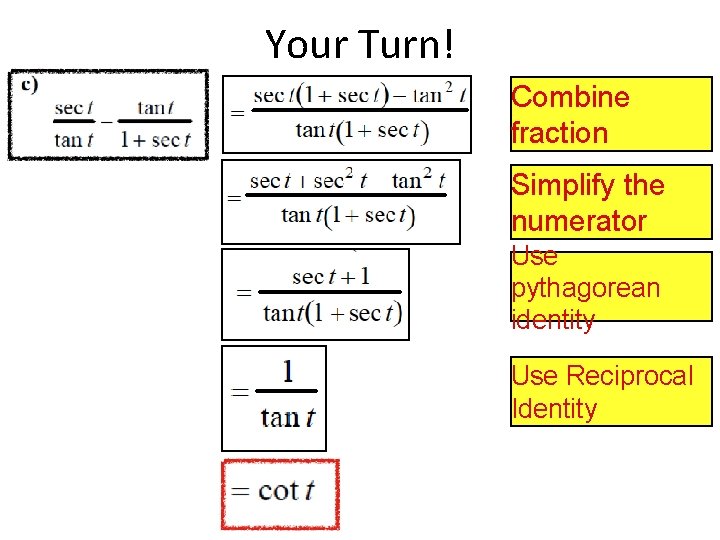
Your Turn! Combine fraction Simplify the numerator Use pythagorean identity Use Reciprocal Identity

Practice 1 cos 2θ cosθ sin 2θ cos 2θ secθ-cosθ csc 2θ cotθ tan 2θ
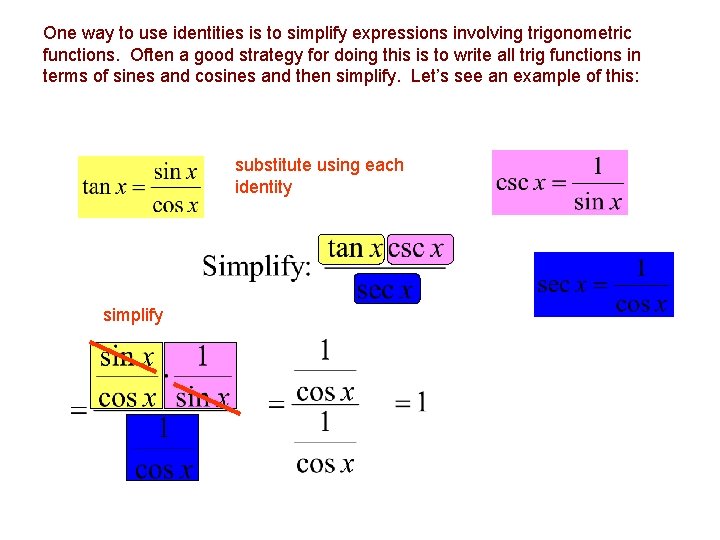
One way to use identities is to simplify expressions involving trigonometric functions. Often a good strategy for doing this is to write all trig functions in terms of sines and cosines and then simplify. Let’s see an example of this: substitute using each identity simplify

Another way to use identities is to write one function in terms of another function. Let’s see an example of this: This expression involves both sine and cosine. The Fundamental Identity makes a connection between sine and cosine so we can use that and solve for cosine squared and substitute.

(E) Examples • Prove tan(x) cos(x) = sin(x) 20

(E) Examples • Prove tan 2(x) = sin 2(x) cos-2(x) 21

(E) Examples • Prove 22

(E) Examples • Prove 23
- Slides: 23