Basic Structural Theory Concepts and construction Forces Vertical

Basic Structural Theory Concepts and construction

Forces Vertical (y-axis only)

Forces Lateral (x-axis only)

Forces Rotational – Moments and Bending

Connections Pin Constrain x & y Rotate freely

Connections Pin Constrain x & y Rotate freely

Connections Pin Constrain x & y Rotate freely

Connections Fixed / Moment-Resisting Constrain x & y Constrain rotation

Connections Fixed / Moment-Resisting Constrain x & y Constrain rotation

Connections Fixed / Moment-Resisting Constrain x & y Constrain rotation

Materials Wood

Materials Wood

Materials Wood – hidden defects

Materials Wood – termite and rot

Materials Wood - flammable

Materials Wood - flammable

Materials Steel

Materials Steel – shapes: Wide Flange

Materials Steel – shapes: American Standard – no longer common

Materials Steel – shapes: Tube

Materials Steel – shapes: Pipe

Materials Steel – shapes: Angle

Materials Steel – shapes: Channel

Materials Steel – shapes: Tee

Materials Steel

Materials Steel

Materials Steel

Materials Steel

Materials Steel – not fireproof

Materials Steel – not fireproof

Materials Steel – fireproofing

Materials Concrete

Materials Concrete

Materials Concrete - CMU

Materials Concrete - CMU

Materials Concrete

Materials Concrete – always steel-reinforced

Materials Concrete – rebar

Materials Concrete – rebar
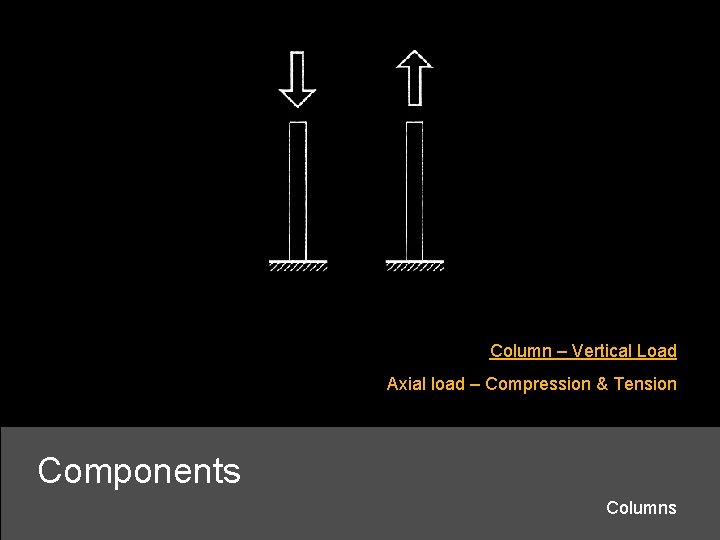
Column – Vertical Load Axial load – Compression & Tension Components Columns

Components Columns - wood
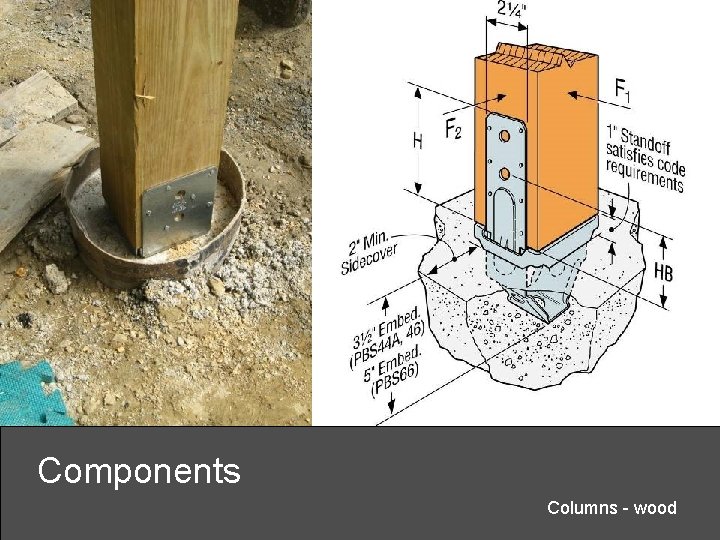
Components Columns - wood

Components Columns - steel

Components Columns - steel

Components Columns - steel

Components Columns - concrete

Components Columns - concrete

Components Columns - concrete

Components Columns – buckling due to compression

Components Columns - buckling

Components Columns - buckling

Components Beams – simply supported (or using pin connections)

Components Beams – deflection is a problem before structural failure occurs

Components Beams – camber to oppose deflection
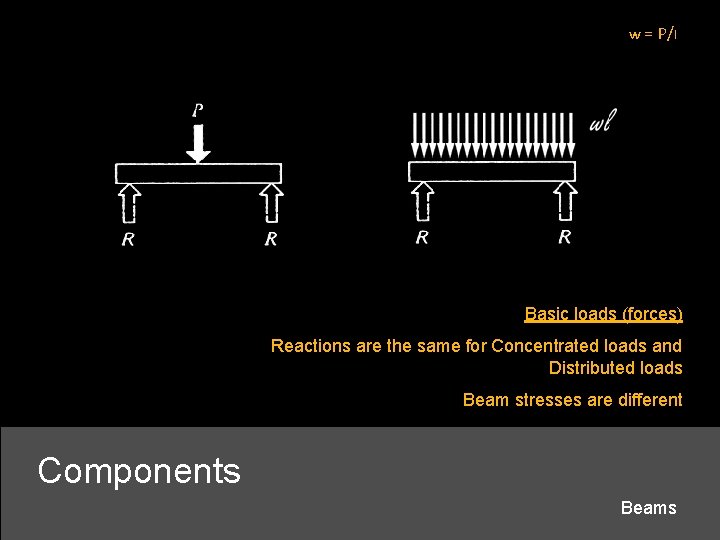
w = P/l Basic loads (forces) Reactions are the same for Concentrated loads and Distributed loads Beam stresses are different Components Beams
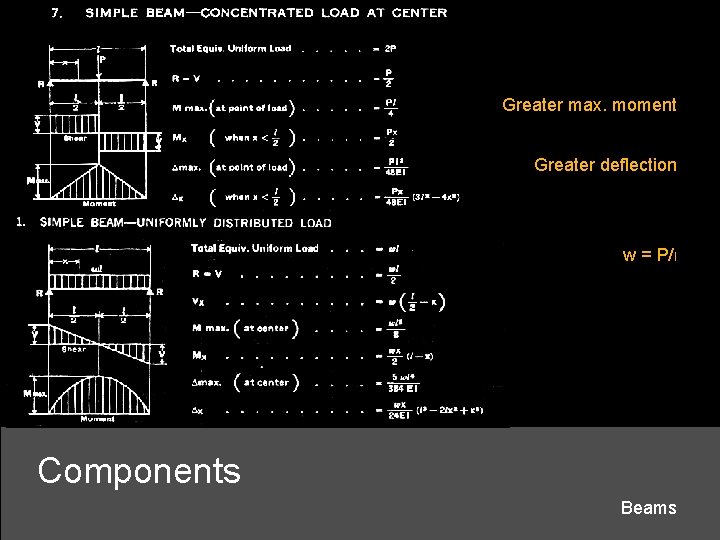
Greater max. moment Greater deflection w = P/l Components Beams
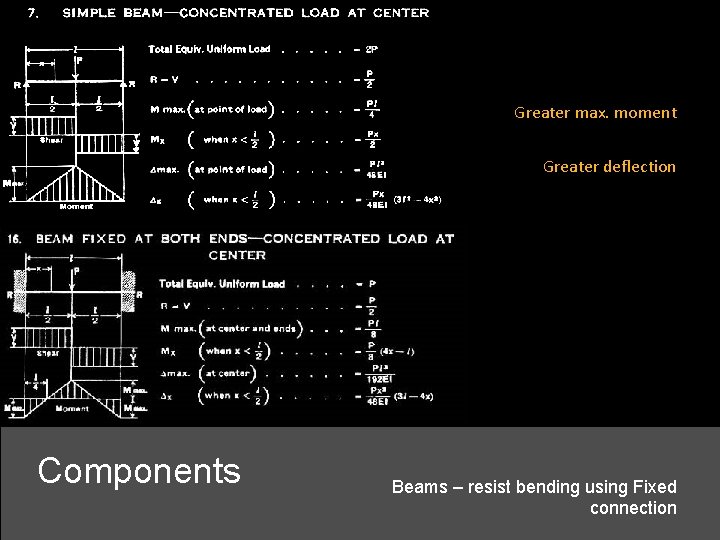
Greater max. moment Greater deflection Components Beams – resist bending using Fixed connection

Greater max. moment Greater deflection Components Beams – resist bending using Fixed connection

Components Beams –Fixed connection

Components Beams –Fixed connection

Components Beams –Fixed connection
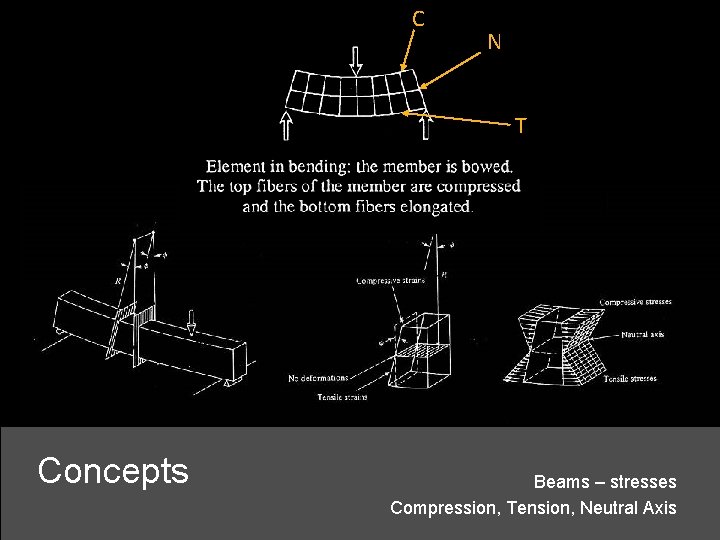
C N T Concepts Beams – stresses Compression, Tension, Neutral Axis

Concepts Beams – stresses Compression, Tension, Neutral Axis

Dmax = Pl 3/48 EI Factors influencing deflection: P = load l= length between supports E = elastic modulus of material (elasticity) I = Moment of inertia (depth/weight of beam) Concepts Beams – controlling deflection

Elastic modulus of materials Density of materials Structural Steel = 200 GPa (29, 023, 300 lb/in 2) Structural Steel = 489 lb/ft 3 Titanium = 110 GPa (15, 962, 850 lb/in 2) Titanium = 282 lb/ft 3 Aluminum = 70 GPa (10, 158, 177 lb/in 2) Aluminum = 169 lb/ft 3 Concrete = 21 GPa (3, 047, 453 lb/in 2) Concrete = 150 lb/ft 3 Douglas Fir = 13 GPa (1, 886, 518 lb/in 2) Douglas Fir = 32 lb/ft 3 Why are titanium and aluminum used in aircraft? Concepts Beams – controlling deflection Elastic modulus – property of material

Yield Strength of materials Density of materials Structural Steel=350 -450 MPa Structural Steel = 489 lb/ft 3 Titanium (Alloy)=900 -1400 MPa Titanium = 282 lb/ft 3 Aluminum=100 -350 MPa Aluminum = 169 lb/ft 3 Concrete=70 MPa (compressive) Concrete = 150 lb/ft 3 Douglas Fir= N/A Douglas Fir = 32 lb/ft 3 1 lb/in 2 = 6891 Pa Concepts Beams – controlling deflection Elastic modulus – property of material

Icc = Moment of inertia of a rectangle about the neutral axis – i. e. it’s centroid = width x height 3 /12 Ixx = Moment of inertia of a rectangle about an axis parallel to the neutral axis = Icc + width x height x (distance between axes)2 Centroid = S (Area x distance to bending axis)/(Total area) Moment of Inertia of beam Dependent on cross-sectional geometry Not dependent on material properties Concepts Beams – controlling deflection Moment of Inertia
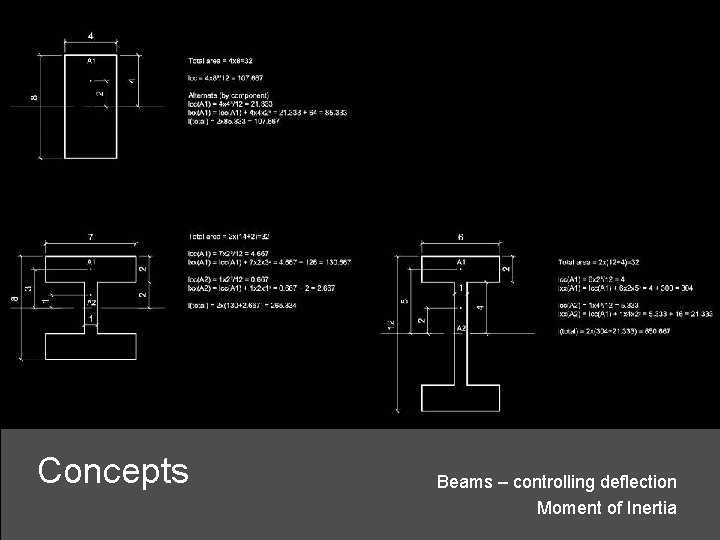
Concepts Beams – controlling deflection Moment of Inertia
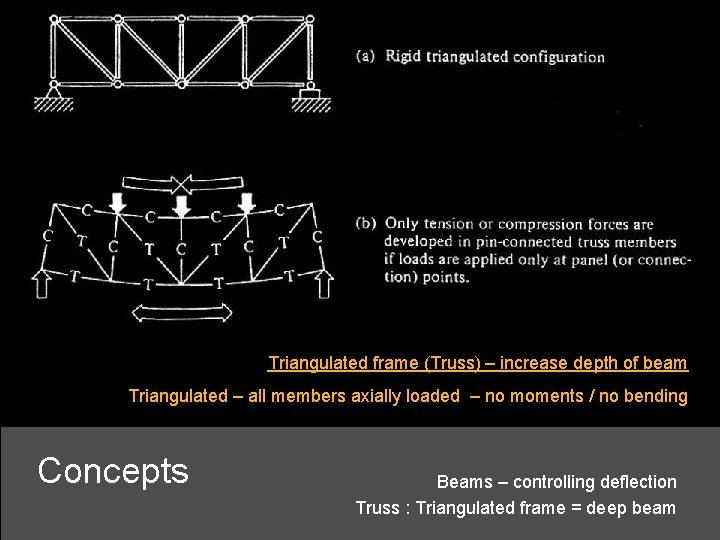
Triangulated frame (Truss) – increase depth of beam Triangulated – all members axially loaded – no moments / no bending Concepts Beams – controlling deflection Truss : Triangulated frame = deep beam

Concepts Beams – controlling deflection Truss : Triangulated frame = deep beam

Components Frames – simple frames

Components Frames – simple frames

Components Frames – simple frames

Components Frames – simple frames – racking due to lateral load

Components Frames – simple frames – racking due to lateral load

Components Frames – shear panel to prevent racking

Components Frames – shear panel to prevent racking
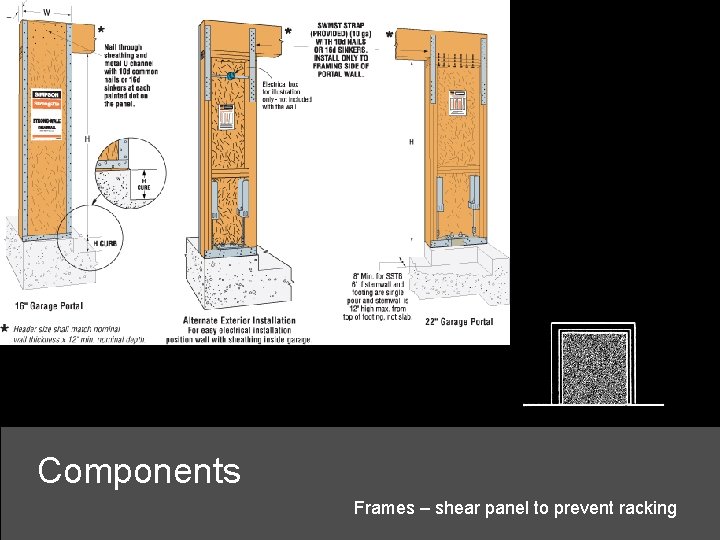
Components Frames – shear panel to prevent racking

Components Frames – shear panel to prevent racking

Components Frames – triangulation to prevent racking

Components Frames – triangulation to prevent racking

Components Frames – triangulation to prevent racking
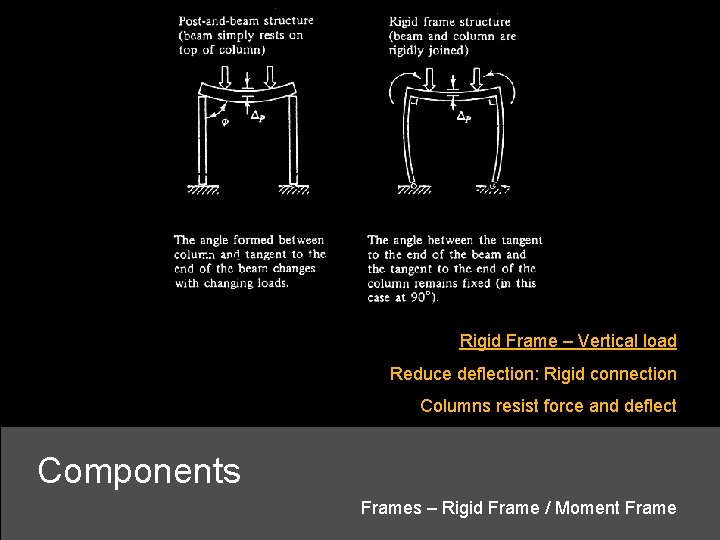
Rigid Frame – Vertical load Reduce deflection: Rigid connection Columns resist force and deflect Components Frames – Rigid Frame / Moment Frame
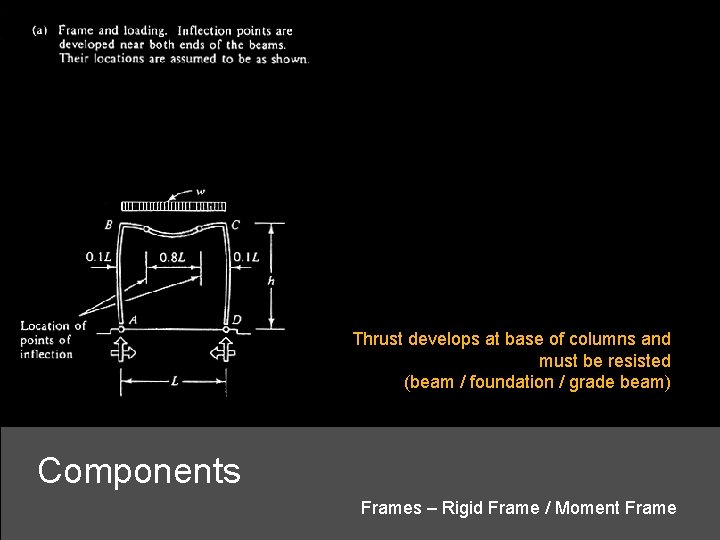
Thrust develops at base of columns and must be resisted (beam / foundation / grade beam) Components Frames – Rigid Frame / Moment Frame

Rigid Frame – Lateral load Resists racking Components Frames – Rigid Frame / Moment Frame

Rigid Frame – Lateral load Resists racking Components Frames – Rigid Frame / Moment Frame

Rigid Frame – Lateral load Resists racking Components Frames – Rigid Frame / Moment Frame

Rigid Frame – Lateral load Resists racking Components Frames – Rigid Frame / Moment Frame
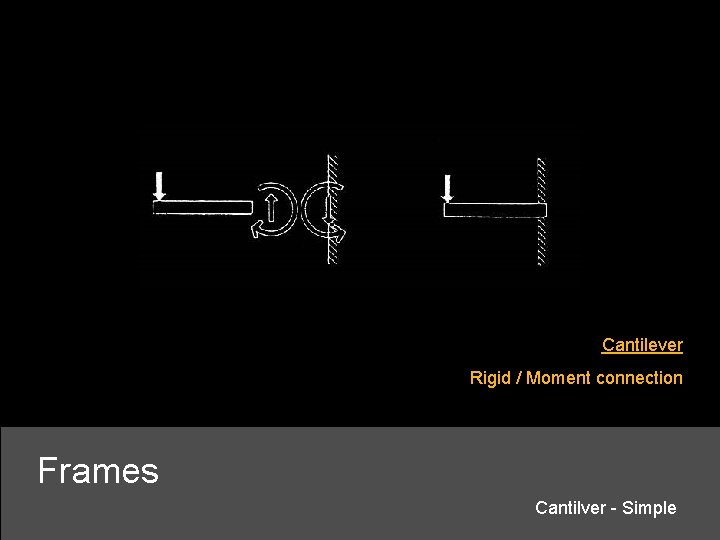
Cantilever Rigid / Moment connection Frames Cantilver - Simple

Frames Cantilver - Simple
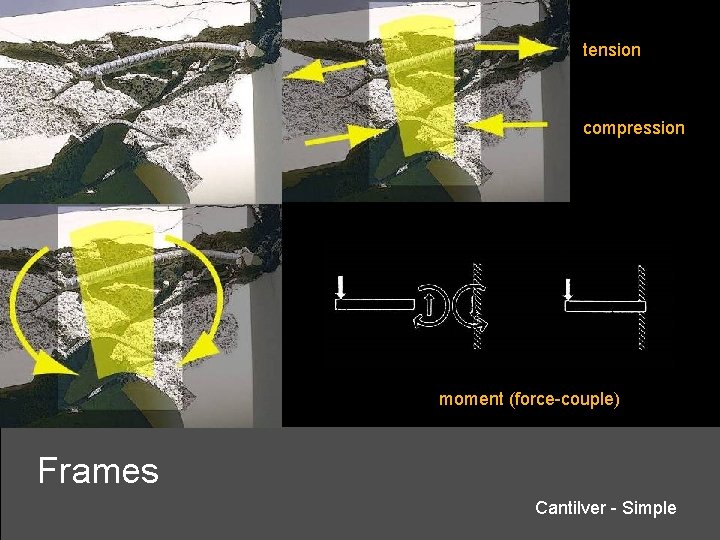
tension compression moment (force-couple) Frames Cantilver - Simple

Greater max. moment Greater deflection Frames Cantilver – Simple More bending stress and deflection than simply supported beam

Lesser max. moment Lesser deflection Frames Cantilver – Backspan Reduces bending stress and deflection without rigid connection

Frames Cantilver – Backspan
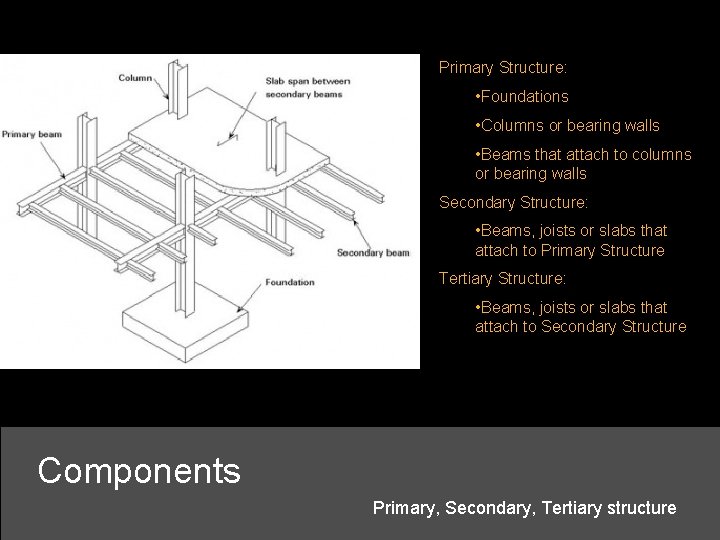
Primary Structure: • Foundations • Columns or bearing walls • Beams that attach to columns or bearing walls Secondary Structure: • Beams, joists or slabs that attach to Primary Structure Tertiary Structure: • Beams, joists or slabs that attach to Secondary Structure Components Primary, Secondary, Tertiary structure
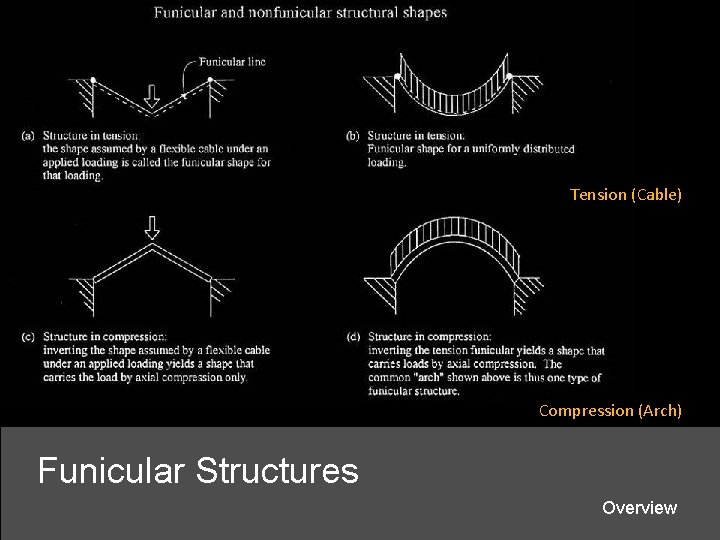
Tension (Cable) Compression (Arch) Funicular Structures Overview

Funicular Structures Cable-suspension

Funicular Structures Tension structures: May include beams to control curves

Funicular Structures Tension structures: Rigid elements acting as fabric Munich Olympic Stadium, Frei Otto

Funicular Structures Inflatable structures

Funicular Structures Inflatable structures

Funicular Structures Arch

Funicular Structures Arch: La Sagrada Familia inverted structural model

Funicular Structures Arch: La Sagrada Familia inverted structural model

Funicular Structures Arch: La Sagrada Familia inverted structural model

Funicular Structures Thin-shell structures El Oceonográfico, Valencia: Felix Candela

Funicular Structures Thin-shell structures: TWA Terminal JFK Airport, Eero Saarinen

Bad things CSUN Parking Structure 1994

Bad things World Trade Center 9/11/2001

Bad things World Trade Center 9/11/2001

Bad things Tacoma Narrows
- Slides: 111