Basic sorting Selection sort Correctness January 18 2019

Basic sorting Selection sort Correctness January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 1

Queue operations • A queue should implement at least the first two of these operations: – enqueue – insert item at the back of the queue – dequeue – remove an item from the front – peek – return the item at the front of the queue without removing it – is. Empty – check if the queue does not contain any items • Like stacks, it is assumed that these operations will be implemented efficiently – That is, in constant time January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 2

Circular arrays • Trick: use a circular array to insert and remove items from a queue in constant time • The idea of a circular array is that the end of the array “wraps around” to the start of the array 7 0 6 0 1 2 3 4 5 6 7 1 2 5 4 January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 3 3

The modulo operator • The mod operator (%) calculates remainders: – 1%5 = 1, 2%5 = 2, 5%5 = 0, 8%5 = 3 • The mod operator can be used to calculate the front and back positions in a circular array – Thereby avoiding comparisons to the array size – The back of the queue is: • (front + num) % arrlength • where num is the number of items in the queue – After removing an item, the front of the queue is: • (front + 1) % arrlength January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien Member attributes: int front; int arrlength; int* arr; int num; 4

Array queue example Queue q; q. enqueue(6); 0 01 front num 6 0 1 2 3 4 5 Insert item at (front + num) % queue. length, then increment num January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 5

Array queue example 210 345 q. enqueue(6); front num q. enqueue(4); q. enqueue(7); q. enqueue(3); q. enqueue(8); 6 4 7 3 8 0 1 2 3 4 Queue q; q. dequeue(); 5 Insert item at (front + num) % queue. length, then increment num Remove item at front, then decrement num and make front = (front + 1) % queue. length January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 6

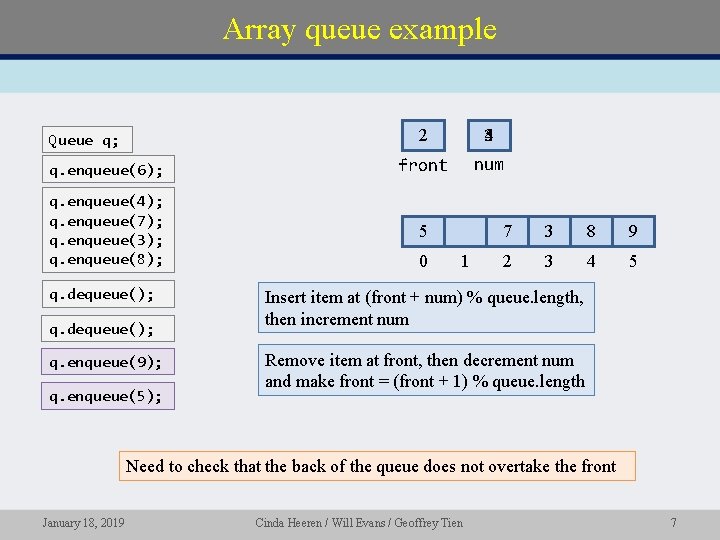
Array queue example 2 543 q. enqueue(6); front num q. enqueue(4); q. enqueue(7); q. enqueue(3); q. enqueue(8); 5 Queue q; q. dequeue(); q. enqueue(9); q. enqueue(5); 0 1 7 3 8 9 2 3 4 5 Insert item at (front + num) % queue. length, then increment num Remove item at front, then decrement num and make front = (front + 1) % queue. length Need to check that the back of the queue does not overtake the front January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 7

Array queue resizing • Suppose we have an array-based queue and we have performed some enqueue and dequeue operations – Then we perform more enqueues to fill the array – How should we resize the array to allow for more enqueue operations? 12 5 76 33 2 41 ? ? front ? January 18, 2019 ? ? ? Cinda Heeren / Will Evans / Geoffrey Tien ? ? 8

Queue implementation Using a Linked List • Removing items from the front of the queue is straightforward • Items should be inserted at the back of the queue in constant time – So we must avoid traversing through the list – Use a second node pointer to keep track of the node at the back of the queue • Requires a little extra administration January 18, 2019 Member attributes: Node* front; Node* back; int num; Cinda Heeren / Will Evans / Geoffrey Tien 9

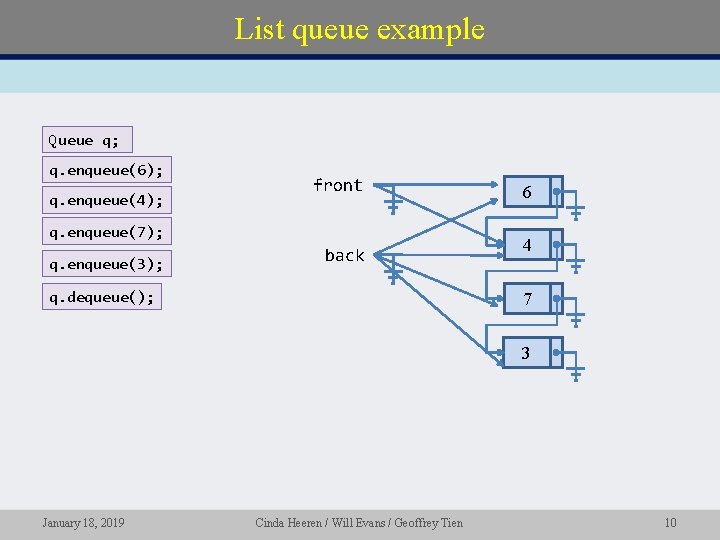
List queue example Queue q; q. enqueue(6); q. enqueue(4); front 6 back 4 q. enqueue(7); q. enqueue(3); q. dequeue(); 7 3 January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 10

Selection sort January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 11

Algorithm analysis – simple sorting Selection sort • January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 12

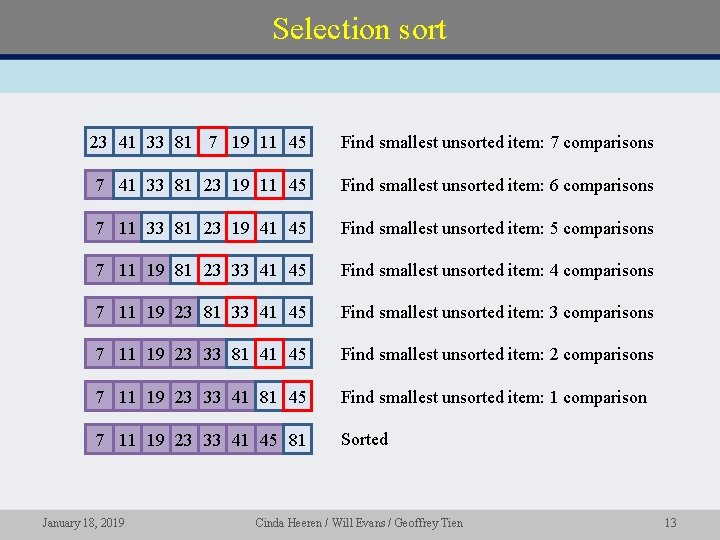
Selection sort 23 41 33 81 7 19 11 45 Find smallest unsorted item: 7 comparisons 7 41 33 81 23 19 11 45 Find smallest unsorted item: 6 comparisons 7 11 33 81 23 19 41 45 Find smallest unsorted item: 5 comparisons 7 11 19 81 23 33 41 45 Find smallest unsorted item: 4 comparisons 7 11 19 23 81 33 41 45 Find smallest unsorted item: 3 comparisons 7 11 19 23 33 81 41 45 Find smallest unsorted item: 2 comparisons 7 11 19 23 33 41 81 45 Find smallest unsorted item: 1 comparison 7 11 19 23 33 41 45 81 Sorted January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 13

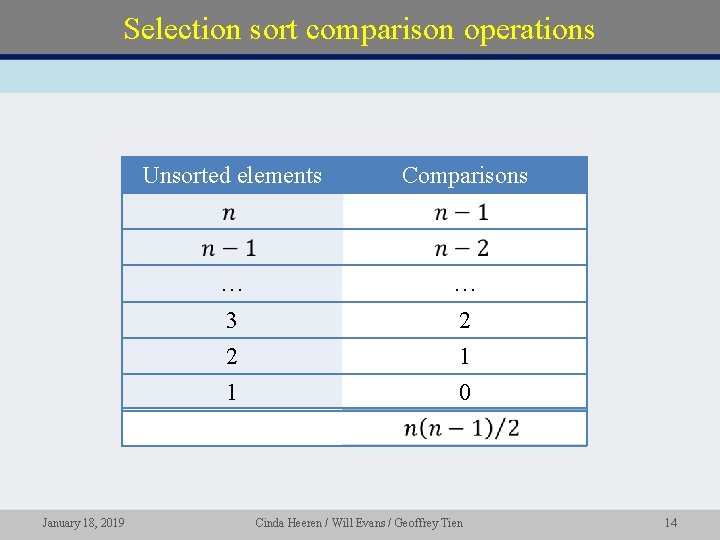
Selection sort comparison operations January 18, 2019 Unsorted elements Comparisons … … 3 2 1 0 Cinda Heeren / Will Evans / Geoffrey Tien 14

Selection sort algorithm void Selection. Sort(vector<int>& arr) { for (int i = 0; i < arr. size() -1; ++i) { int smallest = i; // Find the index of the smallest element for (int j = i + 1; j < arr. size(); ++j) { if (arr[j] < arr[smallest]) { smallest = j; } } // Swap the smallest with the current item temp = arr[i]; { arr[i] = arr[smallest]; arr[smallest] = temp; } } January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 15

Selection sort summary • January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 16

Analyzing loops Proving algorithm correctness using loop invariants • Loop invariants – Properties of the algorithm or structure that are always true (i. e. do not vary) at particular points in the program – Within a loop body, these properties may become violated briefly, but the rest of the loop instructions should fix the properties for the next iteration • E. g. we have an algorithm for Selection sort. How can we prove that it really works for all possible input configurations? January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 17

Selection sort correctness Inner loop • The inner loop's purpose is to identify the index of the smallest value in the unordered portion of the array – use loop invariant to rigourously prove that this happens • A partial inner loop progress: int smallest = i; // Find the index of the smallest element for (int j = i + 1; j < arr. size(); ++j) { if (arr[j] < arr[smallest]) smallest = j; } . . . January 18, 2019 7 9 4 8 12 6 2 5 3 14 15 16 17 20 21 22 18 19 Cinda Heeren / Will Evans / Geoffrey Tien smallest: 16 18

Selection sort Inner loop correctness • January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 19

Selection sort Inner loop correctness • January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 20

Selection sort Inner loop correctness • Now that we know the inner loop works properly, we can prove that the outer loop works properly January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 21

Selection sort Outer loop correctness • The outer loop's purpose is to place the smallest item from the unordered subarray at the end of the ordered subarray • A partial outer loop progress: 2 3 5 6 8 14 25 18 23 10 20 16 0 January 18, 2019 1 2 3 4 5 6 7 Cinda Heeren / Will Evans / Geoffrey Tien 8 9 10 11 22

Selection sort Outer loop correctness • January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 23

Selection sort Outer loop correctness • Why? January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 24

Selection sort Outer loop correctness • January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 25

Readings for this lesson • Carrano & Henry – Chapter 11. 1. 1 (Selection sort) • Epp – Chapter 5. 5 (Loop invariants, correctness) • Next class: – Carrano & Henry: Chapter 11. 1. 3 (Insertion sort) January 18, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 26