Basic Quantities Summary Elliott SI Units The basic

Basic Quantities Summary Elliott

SI Units • The basic seven units • • Metre (m) - length Kilogram (kg) - mass Second (s) - time Kelvin (K) – temperature Ampere (A) - current Mole (mol) – amount of substance Candela (cd) – luminous intensity

Deriving units • HINT – Use formulae or dimensionality • Example – Force • F=ma, where acceleration is measured in metres per second (m s-2) Force is measured in Newtons equivalent to kg m s-2 (mass (kg) x acceleration (m s-2)) • Energy (work done) can be force multiplied by distance Energy is measured in Joules equivalent to kg m 2 s-2 (force (kg m s-2) x distance (m)) • Derived units • Newtons - kg m s-2 • Joules - kg m 2 s-2 • Watt - kg m 2 s-3 • Pressure - kg m-1 s-2 • Coulomb - A s • Hertz - s-1

Heat and Temperature • Heat • The amount of thermal (movement of molecules) energy in a substance • Measured in Joules • Temperature • A measure of how hot or cold an object is • Measured in degrees Celsius or degrees Kelvin

Newton’s Laws •

Estimation • Extremely important in assessing whether calculations are likely to be correct • Some important rough values (measured to 1 significant figure) to be used in estimations are: • • Speed of light ≈ 3 x 108 m s-1 Speed of sound ≈ 300 m s-1 Mass of Earth ≈ 6 x 1024 kg Acceleration due to gravity (g) on Earth ≈ 10 m s-2 Radius of Earth ≈ 6 x 106 m (6000 km) Density of water ≈ 1000 kg m-3 (1 g cm-3) Atmospheric pressure ≈ 100000 kg m-1 s-2 (100000 Pa)

Accuracy and precision • Accuracy • How close the value you measure is to the actual value (the standard or accepted value) • Description of systematic errors • Example – A measurement is accurate if the set up is well calibrated, a ruler that starts 1 mm too early can never be accurate to within 1 mm. • Precision High accuracy, low precision • How close it would be possible to get to a correct value due to the equipment used • Description of random errors • Example – Assuming perfect calibration there is still a limit to precision, a watch that has a second hand can never be more precise than a second. High precision, low accuracy

Vectors and scalars • Scalars • A measurement with just magnitude (and units) • Examples – mass, length, speed, temperature, energy, power, etc. • E. g. A ball has mass 2 kg A ball has a speed of 30 m s-1 • Vectors • A measurement with magnitude and direction • Examples – weight, displacement, velocity, force, momentum, etc. • E. g. A ball has a weight of 20 N downwards (towards Earth) A ball has a velocity of 30 m s-1 in a North-Easterly direction A ball has a velocity of 15 m s-1 in a direction 30 o from the horizontal

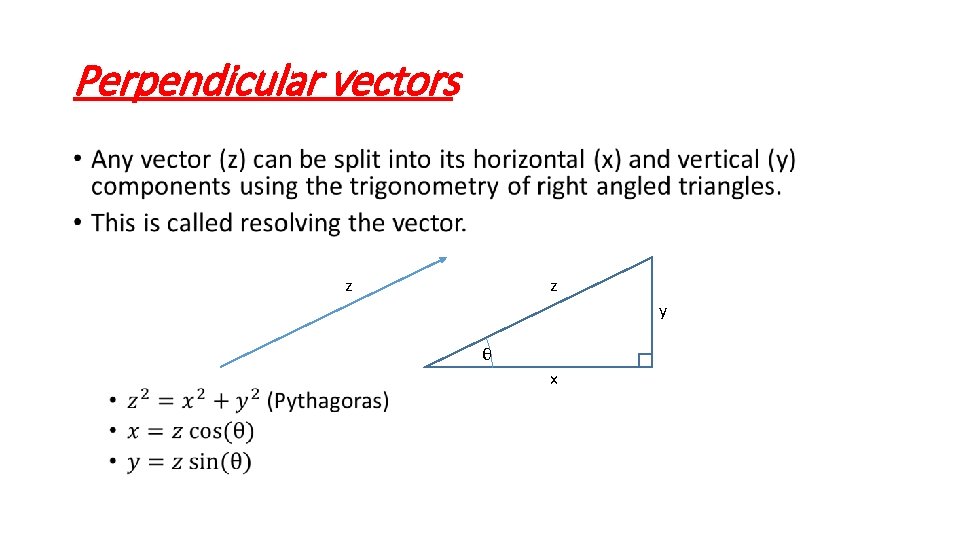
Perpendicular vectors • z z y θ x

Vectors (continued) • Any two vectors can be added in two ways • Add the two horizontal and the two vertical components together once resolved • If a = xi + yj and b = ui + vj (in vector notation); a + b = (x+u)i + (y+v)j a – b = (x-u)i + (y-v)j b – a = (u-x)i + (v-y)j -a – b = (-x-u)i + (-y-v)j = -(a+b) • • In vector notation i and j represent unit vectors, i. e. one unit in the x direction and one unit in the y direction respectively • Find the resultant of the lines • A negative vector is one in the opposite direction -b b a b -a -b -a a b-a a-b a+b -a a b -b

Vectors (continued) • Equilibrium • A body is in equilibrium (has no resultant force on it) if the vectors add up to a closed triangle • Example – The object below would continue at constant speed Thrust 500 N Weight 300 N 36. 9 o • Multiplying vectors Drag 400 N • You can multiply a vector by a scalar – this will multiply the magnitudes and leave the direction the same • You can’t multiply a scalar by a vector (you can multiply a vector but it is beyond the A-Level syllabus)