Basic Principles of Science What is Science Accuracy

Basic Principles of Science What is Science? Accuracy and Precision Units of Measurement Scientific Notation Significant Figures

What is Science? The effort to understand how the physical world works. SCIENCE NOT SCIENCE Astronomy Astrology Physics Magic Neurology Palm Reading Chemistry Alchemy Evolution Creationism Science can only be applied to natural events. It cannot be used to support or disprove opinions, beliefs or the truly supernatural. Because of this, science makes no comment on philosophy, religion, and morality.

What are Chemistry and Physics? Chemistry is the study of the composition of matter and the changes that matter undergoes. Physics is the study of the natural world, matter and energy and how the are related. These two fields are closely related.

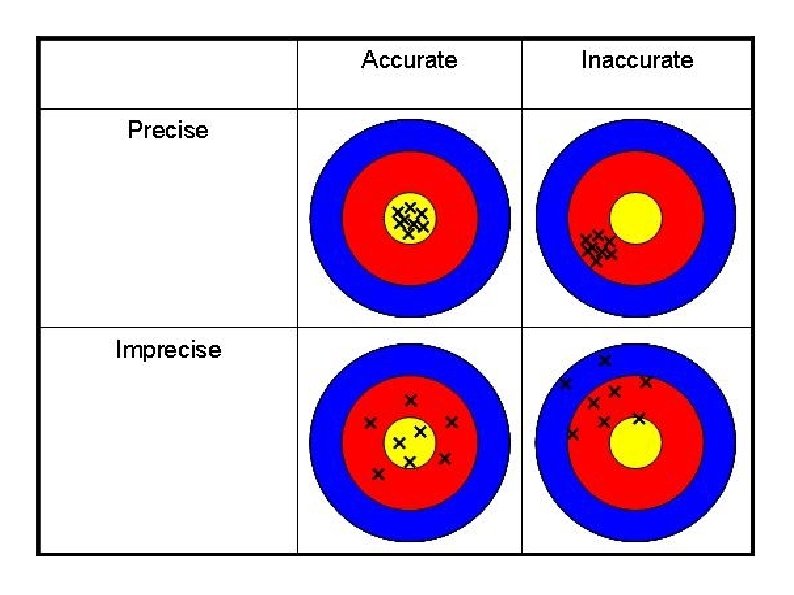
Accuracy and Precision In science, measurements are vital for the advancement of knowledge. Because of this, numbers involved in raw or statistical data must be accurate and precise. Accuracy is a measure of how close a measurement comes to the actual or true value of whatever is measured. Precision is a measure of how close a series of measurements are to one another.

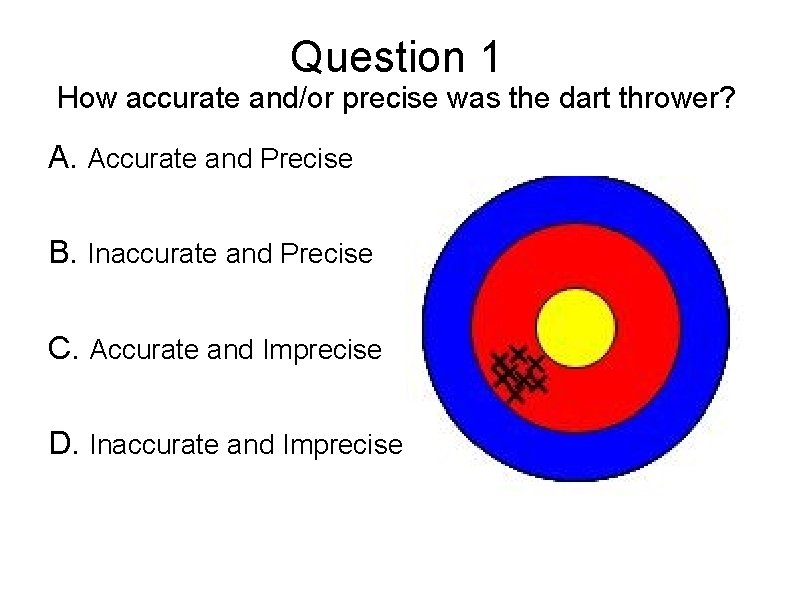
Question 1 How accurate and/or precise was the dart thrower? A. Accurate and Precise B. Inaccurate and Precise C. Accurate and Imprecise D. Inaccurate and Imprecise

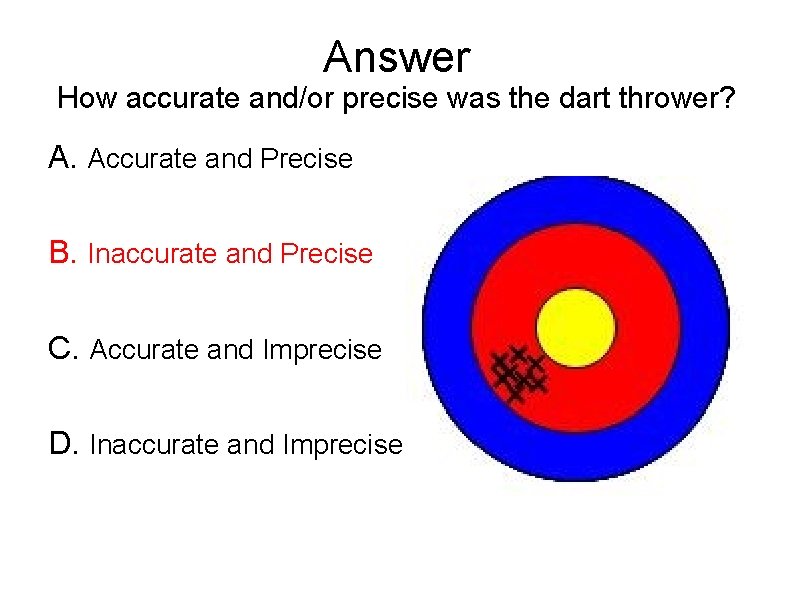
Answer How accurate and/or precise was the dart thrower? A. Accurate and Precise B. Inaccurate and Precise C. Accurate and Imprecise D. Inaccurate and Imprecise

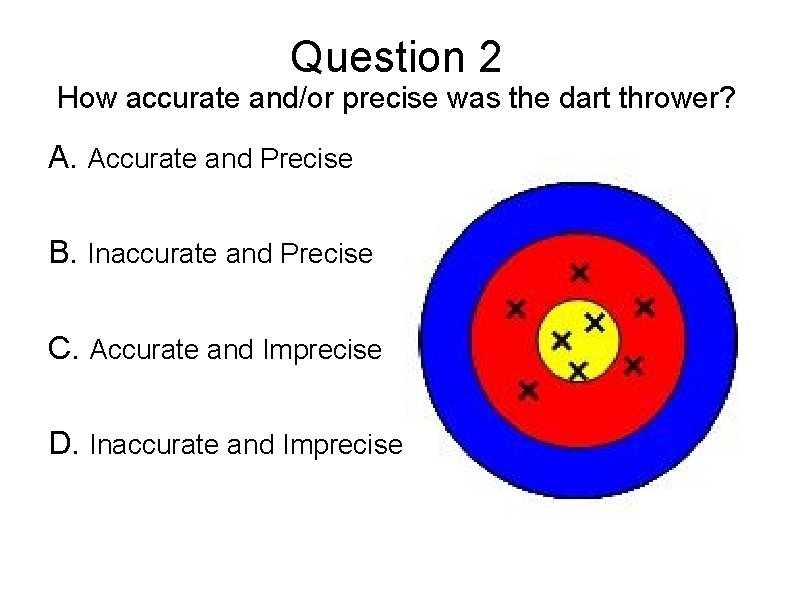
Question 2 How accurate and/or precise was the dart thrower? A. Accurate and Precise B. Inaccurate and Precise C. Accurate and Imprecise D. Inaccurate and Imprecise

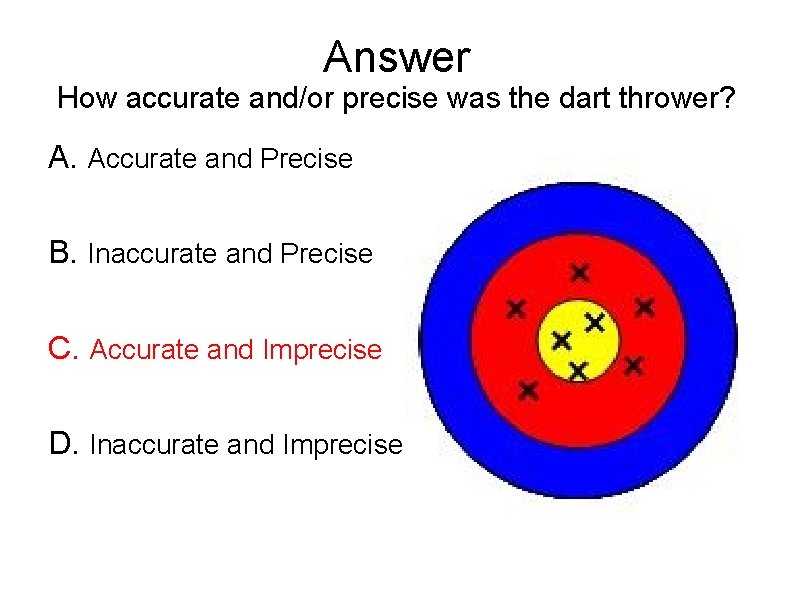
Answer How accurate and/or precise was the dart thrower? A. Accurate and Precise B. Inaccurate and Precise C. Accurate and Imprecise D. Inaccurate and Imprecise

Units of Measurement In science, measurements are made in an improved version of the metric system; the International System of Units (or SI Units) used and understood by scientists worldwide. SI BASE UNITS Length (meters “m”) Mass (kilogram “kg”) Time (seconds “s”) Temperature (Kelvin “K”) Amount of Substance (moles “mol”)

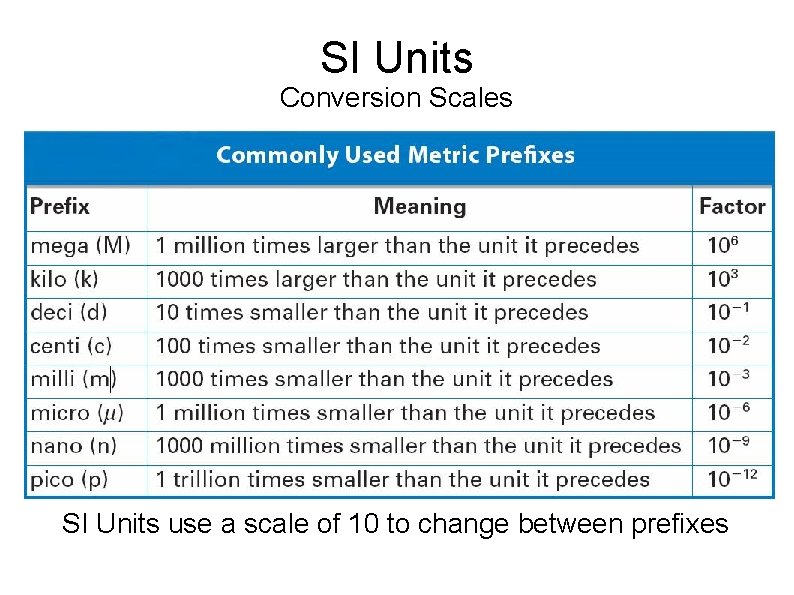
SI Units Conversion Scales SI Units use a scale of 10 to change between prefixes

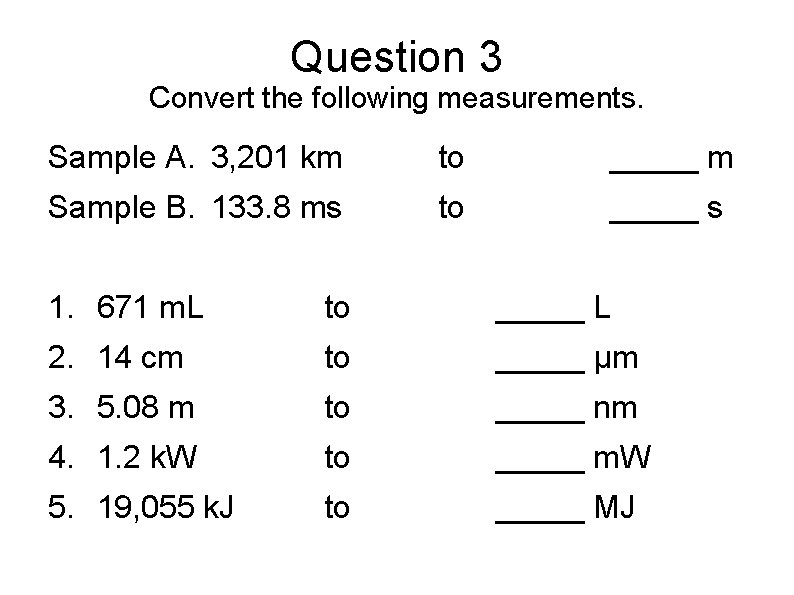
Question 3 Convert the following measurements. Sample A. 3, 201 km to _____ m Sample B. 133. 8 ms to _____ s 1. 671 m. L to _____ L 2. 14 cm to _____ µm 3. 5. 08 m to _____ nm 4. 1. 2 k. W to _____ m. W 5. 19, 055 k. J to _____ MJ

Question 3 Convert the following measurements. Sample A. 3, 201 km to 3, 201, 000 m Sample B. 133. 8 ms to 0. 1338 s 1. 671 m. L to _____ L 2. 14 cm to _____ µm 3. 5. 08 m to _____ nm 4. 1. 2 k. W to _____ m. W 5. 19, 055 k. J to _____ MJ

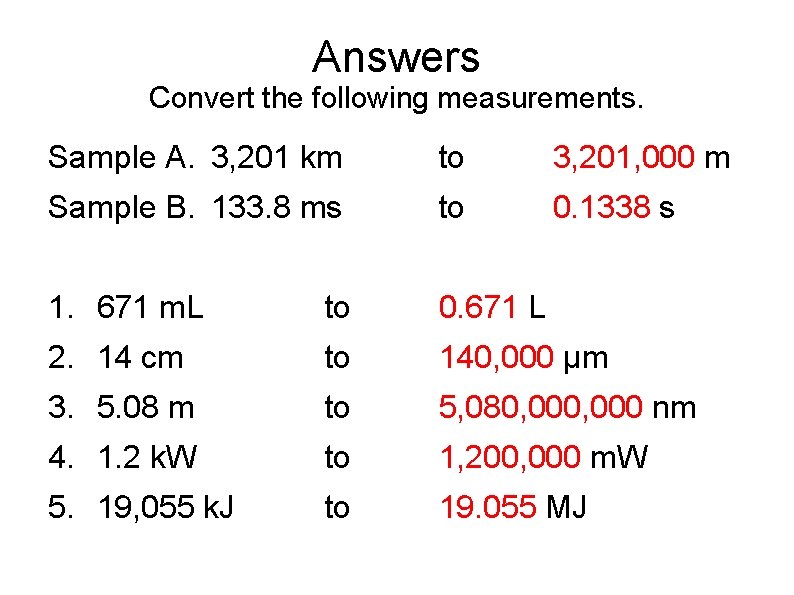
Answers Convert the following measurements. Sample A. 3, 201 km to 3, 201, 000 m Sample B. 133. 8 ms to 0. 1338 s 1. 671 m. L to 0. 671 L 2. 14 cm to 140, 000 µm 3. 5. 08 m to 5, 080, 000 nm 4. 1. 2 k. W to 1, 200, 000 m. W 5. 19, 055 k. J to 19. 055 MJ

Scientific Notation In science (and particularly chemistry) you encounter very large or very small numbers. Examples: 1 gram of Hydrogen contains approximately 602, 000, 000, 000 atoms A single atom of Gold has an approximate mass of 0. 000 000 327 gram For this reason, a shorthand system for writing sizable numbers is used. Scientific Notation is an expression of numbers in the form m × 10 n where m is between 1 and 10, and n is an integer.

Scientific Notation To convert numbers into scientific notation, move the decimal until there is only one nonzero number in front of it. The number of moves is equal to the exponent.

Question 4 Change these numbers to scientific notation. Sample A. 3, 071, 000 to ____ Sample B. 0. 0014 to ____ 1. 6500 to ____ 2. 0. 000 2 to ____ 3. -137. 7 to ____ 4. 1, 200, 009 to ____ 5. 0. 000 636 to ____

Question 4 Change these numbers to scientific notation. Sample A. 3, 071, 000 to 3. 071 x 106 Sample B. 0. 0014 to 1. 4 x 10 -3 1. 6500 to ____ 2. 0. 000 2 to ____ 3. -137. 7 to ____ 4. 1, 200, 009 to ____ 5. 0. 000 636 to ____

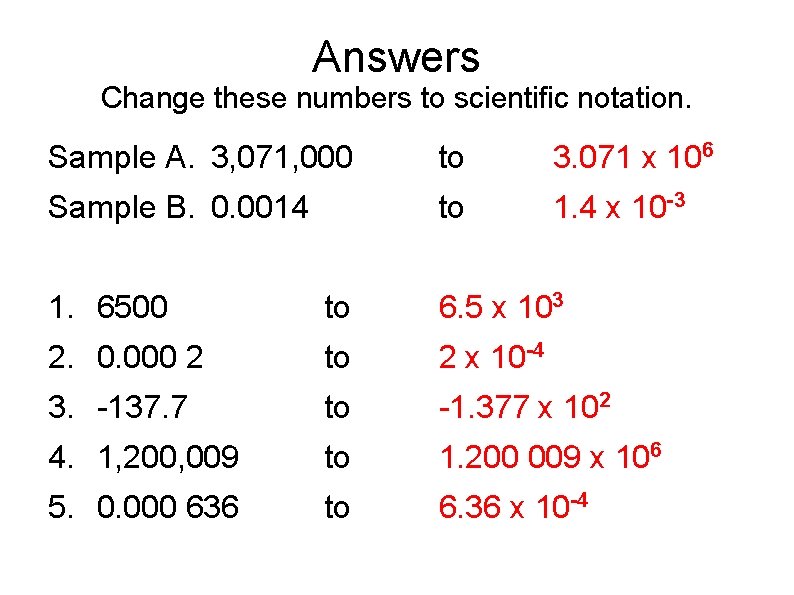
Answers Change these numbers to scientific notation. Sample A. 3, 071, 000 to 3. 071 x 106 Sample B. 0. 0014 to 1. 4 x 10 -3 1. 6500 to 6. 5 x 103 2. 0. 000 2 to 2 x 10 -4 3. -137. 7 to -1. 377 x 102 4. 1, 200, 009 to 1. 200 009 x 106 5. 0. 000 636 to 6. 36 x 10 -4

Significant Figures When measuring, the exactness of your measurements are very important. To determine which figures are important, we use the five rules of significant figures. All the digits that can be known precisely in a measurement are significant figures. Significant figures must be determined before converting numbers into scientific notation.

Rules of Significant Figures 1. All non-zero numbers (1 -9) ARE significant. 2. All zeros between non-zeros ARE significant. Example: 1001 has four significant figures. 3. Leftmost zeros in front of non-zeros ARE NOT. Example: 0. 000032 has two significant figures.

Rules of Significant Figures 4. Zeros at the end of a number and to the right of a decimal point ARE significant. Example: 450. 0 and 1. 020 have four significant figures. NOTE – the number MUST have a decimal point 5. Zeros at the rightmost end of a number and are left of an 'understood decimal point' ARE NOT. Example: 1 000 and 60 000 have one significant figure.

Question 5 How many significant figures are in these numbers? Sample A. 3002. 0 has ____ Sample B. 0. 00 670 has ____ 1. 223 has ____ 2. 1 000. 0 has ____ 3. 0. 05070 has ____ 4. 300. has ____ 5. 0. 0 074 010 has ____

Question 5 How many significant figures are in these numbers? Sample A. 3002. 0 has five Sample B. 0. 00 670 has three 1. 223 has ____ 2. 1 000. 0 has ____ 3. 0. 05070 has ____ 4. 300. has ____ 5. 0. 0 074 010 has ____

Answers How many significant figures are in these numbers? Sample A. 3002. 0 has five Sample B. 0. 00 670 has three 1. 223 has three 2. 1 000. 0 has eight 3. 0. 05070 has four 4. 300. has three 5. 0. 0 074 010 has five

Multiplying in Scientific Notation When multiplying numbers in scientific notation, the first two integers multiplied as normal. The exponents are added NOT MULTIPLIED. If the number at the front becomes larger than 10, move the decimal to the left and add one to the exponent. The significant figures of your answer may not be greater than the SMALLEST number of significant figures in the factors. Example (2. 1 x 103) x (5. 2 x 105)

Multiplying in Scientific Notation (2. 1 x 103) x (5. 2 x 105) multiply the first numbers 2. 1 x 5. 2 = 10. 92 adjust for significant figures 10. 92 ~ 11 add the exponents 3+5=8 put together 11 x 108 adjust the first number 1. 1 x 109

Dividing in Scientific Notation When Dividing numbers in scientific notation, the first two integers divided as normal. The exponents are subtracted NOT DIVIDED. If the number at the front becomes smaller than 1, move the decimal to the right and subtract one from the exponent. The significant figures of your answer may not be greater than the SMALLEST number of significant figures in the quotients. Example (3. 5 x 106) / (5. 6 x 102)

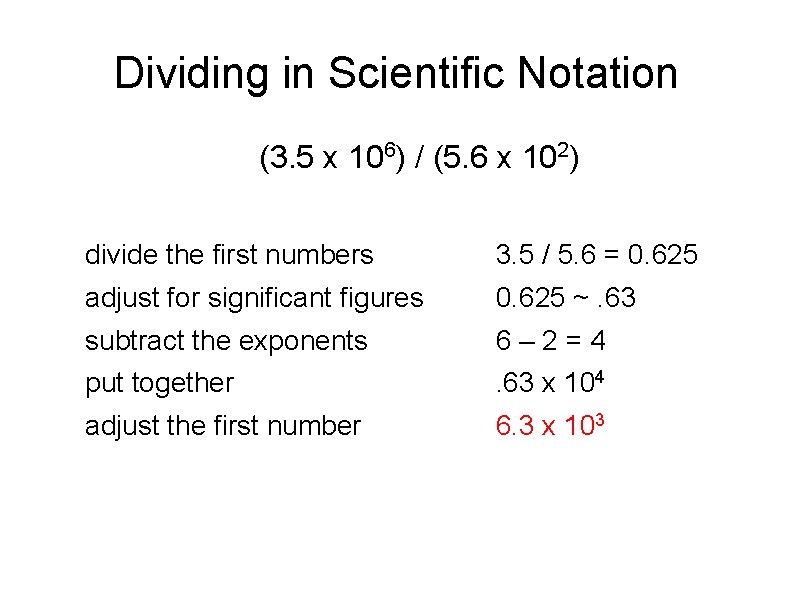
Dividing in Scientific Notation (3. 5 x 106) / (5. 6 x 102) divide the first numbers 3. 5 / 5. 6 = 0. 625 adjust for significant figures 0. 625 ~. 63 subtract the exponents 6– 2=4 put together . 63 x 104 adjust the first number 6. 3 x 103

CLASSWORK Calculate the answers to these problems 1) (4 x 106) / (2 x 102) 2) (1. 5 x 102) x (4 x 107) 3) (3. 7 x 10 -3) / (-1. 9 x 10 -8) 4) (4. 71 x 10 -3) x ( 5. 89 x 103)