Basic Perspective Projection Watt Section 5 2 some

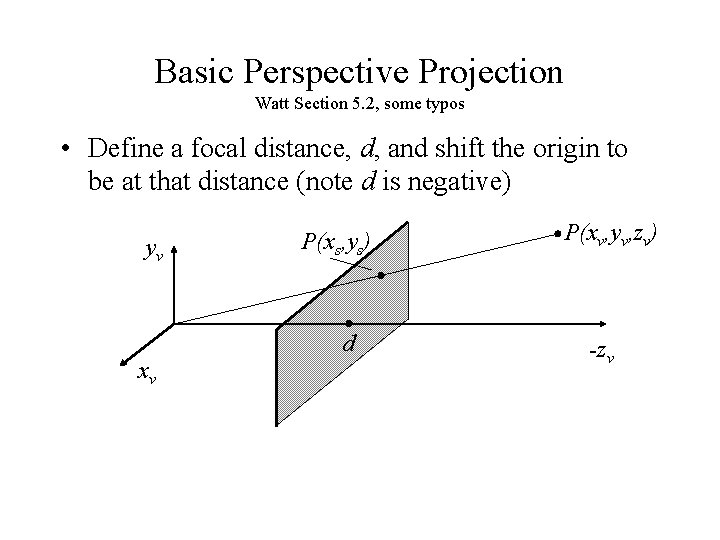
Basic Perspective Projection Watt Section 5. 2, some typos • Define a focal distance, d, and shift the origin to be at that distance (note d is negative) yv P(xs, ys) d xv P(xv, yv, zv) -zv

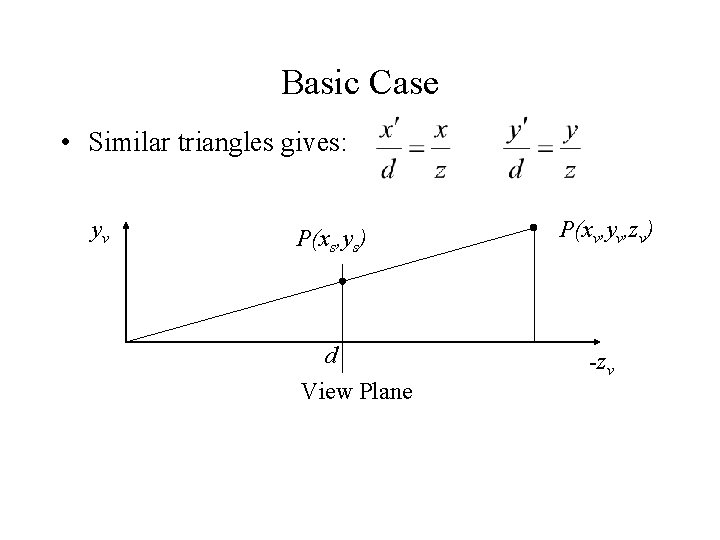
Basic Case • Similar triangles gives: yv P(xs, ys) d View Plane P(xv, yv, zv) -zv

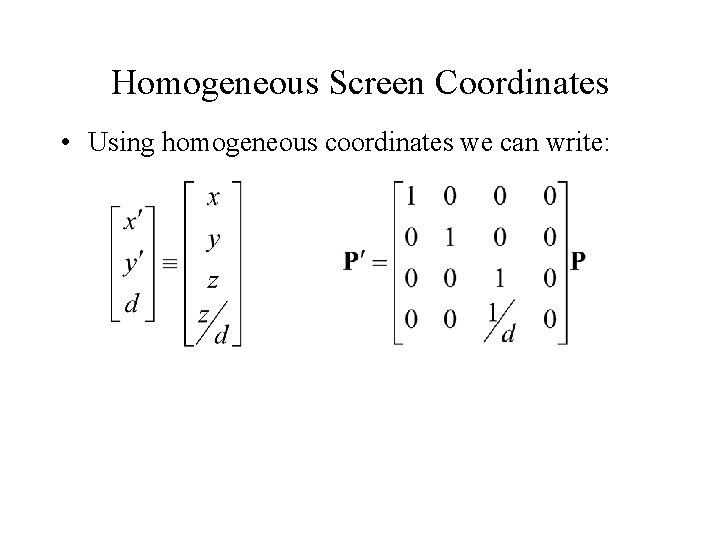
Homogeneous Screen Coordinates • Using homogeneous coordinates we can write:

Clipping Planes • The image has a finite width and height • Edges define clipping planes that cut off geometry outside the view • Also define near and far clipping planes – Clip things behind the camera and very distant – Far plane can be problematic: Use tricks like “fog” to blend it out

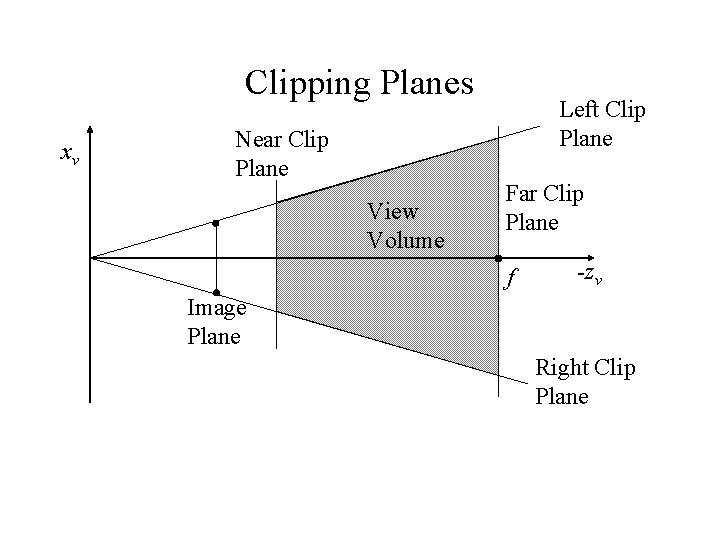
Clipping Planes xv Near Clip Plane View Volume Left Clip Plane Far Clip Plane f -zv Image Plane Right Clip Plane

Open. GL Basic Case • glu. Perspective(…) – Field of view (determines focal distance) – Aspect ratio (should match window aspect ratio) – Near and far clipping planes • Assumes that the image is centered in the image plane

Screen Space • Image corners should be (-1, -1), (1, 1) instead of (-w, -h), (w, h) • We need depth information to decide what’s in front • Useful properties: – Points on the image plane should map to zs=0 – Points on the far clip plane should map to zs=1 – Intersections of lines and planes in view space should map to their intersections in screen space • Straight lines should transform to straight lines • Planes should transform to planes

Computing Screen Depth • Intersections pts maintained if: zs=A+B/zv • Desired mapping of image plane and far plane gives constraints. Solving equation gives:

Homogeneous Screen Coords • Using homogeneous coordinates we can write: • Note: ws is homogeneous coordinate, w is window width

Decomposing the Transformation • The transformation taking view to screen space can be decomposed into two components: – One scales the space to make the side clipping planes of the form x=z, y=z – The other deforms space to take the frustum to a box, with the focal point at -

Small Complication • We really want the near clip plane to map to zs=0 • Change focal dist to near clip dist, modify image size (or specify field of view and derive image size) Image Plane New Image Plane

General Case • Previous case assumed that view window was centered with corners (-w, -h), (w, h) • General case uses arbitrary area on image plane (xmin, ymin), (xmax, ymax) • Open. GL: gl. Frustum(. . . ) – Corners of frustum in image plane – Near and far clip planes

General to Basic Case • Shear the volume so that the central axis lies on the n-axis – This is a shear, because rectangles on planes n=constant must stay rectangles • Shear takes old window midpoint to (0, 0, d) - this means that matrix is:

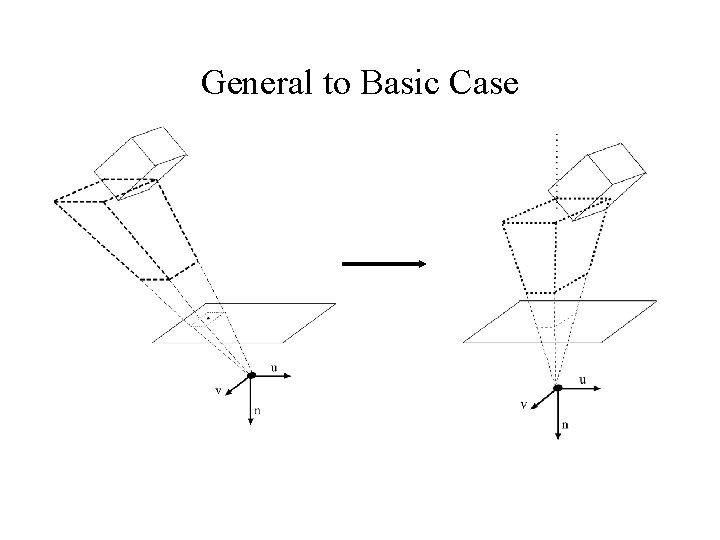
General to Basic Case

Near/Far and Depth Resolution • It may seem sensible to specify a very near clipping plane and a very far clipping plane – Sure to contain entire scene • But, a bad idea: – Open. GL only has a finite number of bits to store screen depth – Too large a range reduces resolution in depth - wrong thing may be considered “in front” • Distant stuff is very small anyway!

Screen to Window Space • Points in screen space are in homogeneous form – Clipping (described next) must be done in this form • “Perspective divide”, converts homogeneous points into 3 D screen points – x, y range from – 1 to 1, z from 0 to 1 – Do lighting here • Viewport transformation scales and translates x, y to fill the window in the screen: gl. Viewport(…)

Viewing Transformation Summary • Convert world to view: Translation and rotation • Convert view to screen: Translation, possibly shearing, scaling and perspective • Convert screen to window: Scale and translate • All managed by Open. GL – You just give the parameters

Clipping • Parts of the geometry to be rendered may lie outside the view volume – View volume maps to memory addresses – Out-of-view geometry generates invalid addresses • Clipping removes parts of the geometry that are outside the view • Best done in screen space before perspective divide

Clipping (2) • Points are trivial to clip - just check which side of the clip planes they are on (dot product) • Many algorithms for clipping lines exist – Next lecture • Two main algorithms for clipping polygons exist – Sutherland-Hodgman (today) – Weiler (next lecture)

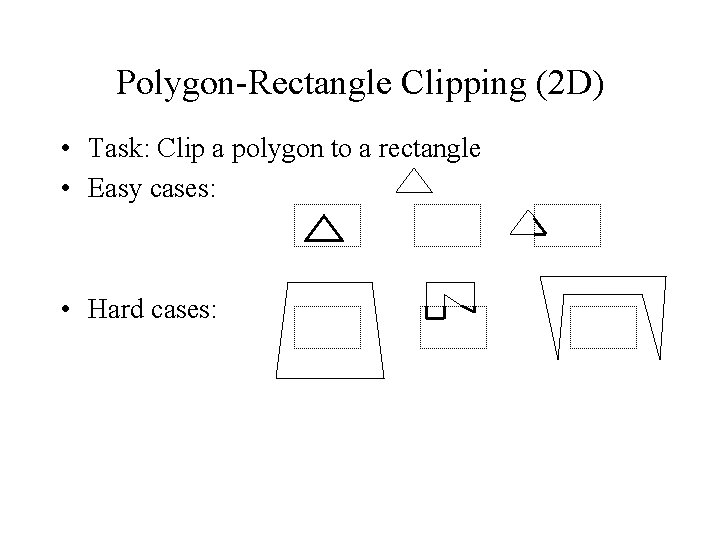
Polygon-Rectangle Clipping (2 D) • Task: Clip a polygon to a rectangle • Easy cases: • Hard cases:

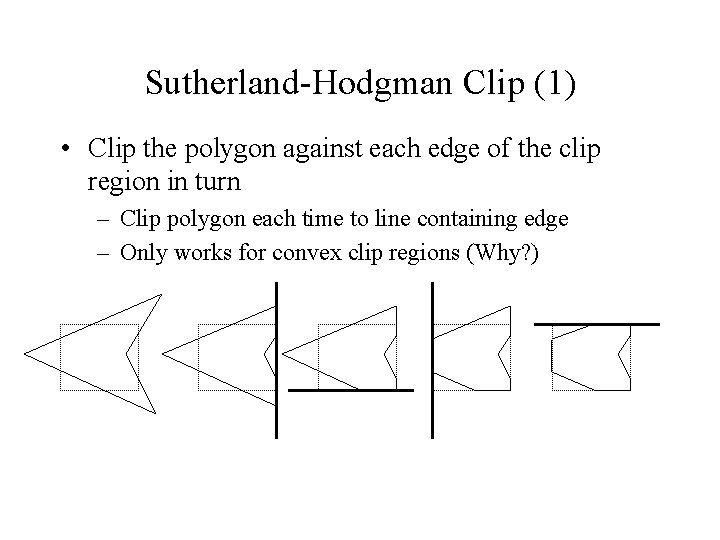
Sutherland-Hodgman Clip (1) • Clip the polygon against each edge of the clip region in turn – Clip polygon each time to line containing edge – Only works for convex clip regions (Why? )

Sutherland-Hodgman Clip (2) • To clip a polygon to a line: – Consider the polygon as a list of vertices – One side of the line is inside the clip region, the other outside – Think of the process as rewriting the polygon, one vertex at a time – Check start vertex: if “inside”, emit it, otherwise ignore it – Process vertex list proceeding as follows…

Sutherland-Hodgman (3) • Look at the next vertex in the list: – polygon edge crosses clip edge going from out to in: output crossing point, next vertex – polygon edge crosses clip edge going from in to out: output crossing – polygon edge goes from out to out: output nothing – polygon edge goes from in to in: output next vertex

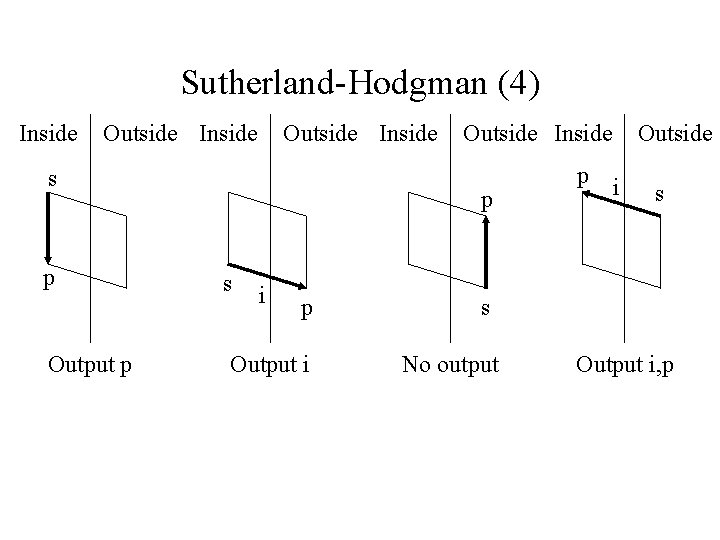
Sutherland-Hodgman (4) Inside Outside Inside s p Output p Outside Inside p s i p Output i p Outside i s s No output Output i, p

Sutherland-Hodgman (5) • In 3 D, clip against planes instead of lines – Six planes to clip against – Inside/Outside test still works • Suitable for hardware implementation – Only need the clip edge, the endpoints of the current edge, and the last output point – Polygon edges are output as they are found, and passed right on to the next clip region edge