Basic Performance Parameters in Computer Architecture Good Old

Basic Performance Parameters in Computer Architecture:





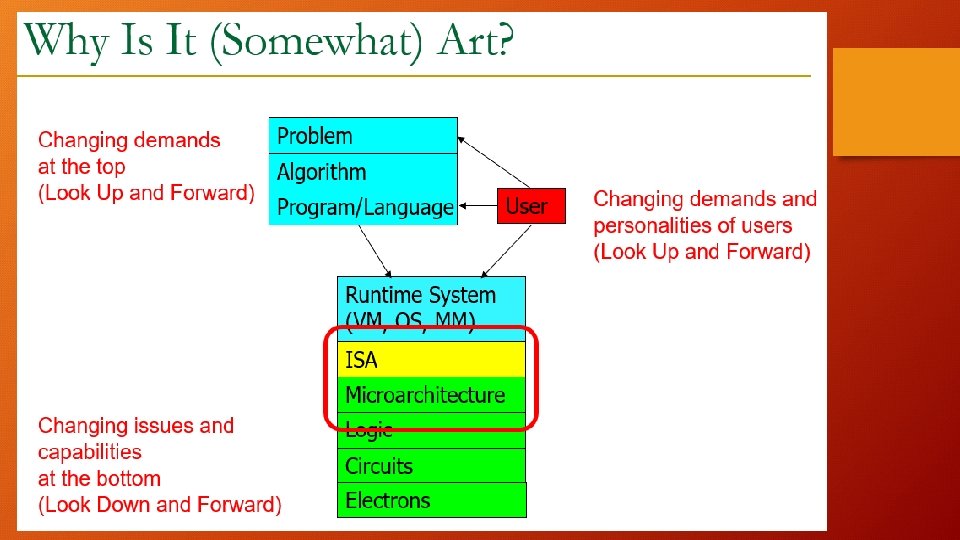

Good Old Moore’s Law: (Technology vs Architects) • For every 18 -24 months, 2 x transistors on the same chip area. • Processor Speed Doubles every 18 -24 months • Energy Operation halves every 18 -24 months • Memory Capacity doubles every 18– 24 months
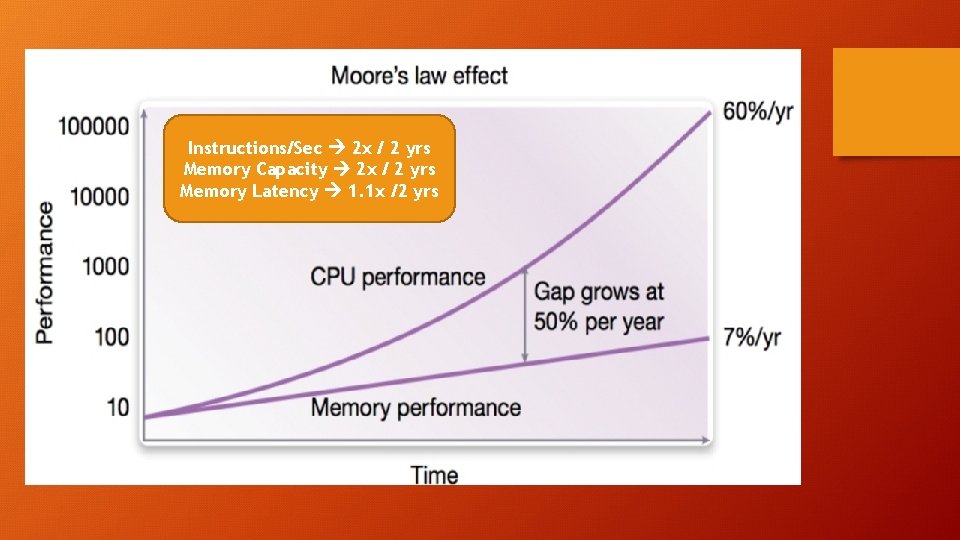
Instructions/Sec 2 x / 2 yrs Memory Capacity 2 x / 2 yrs Memory Latency 1. 1 x /2 yrs
Cache Magic

Parameters for Metric and Evaluation: What does better mean in Computer Architecture? Is the speed (GHz) or the Memory size(GB)? Latency and Throughput are two key performance parameters. Latency: time taken from start to end for a process Throughput: Number of computations per second (#/second)
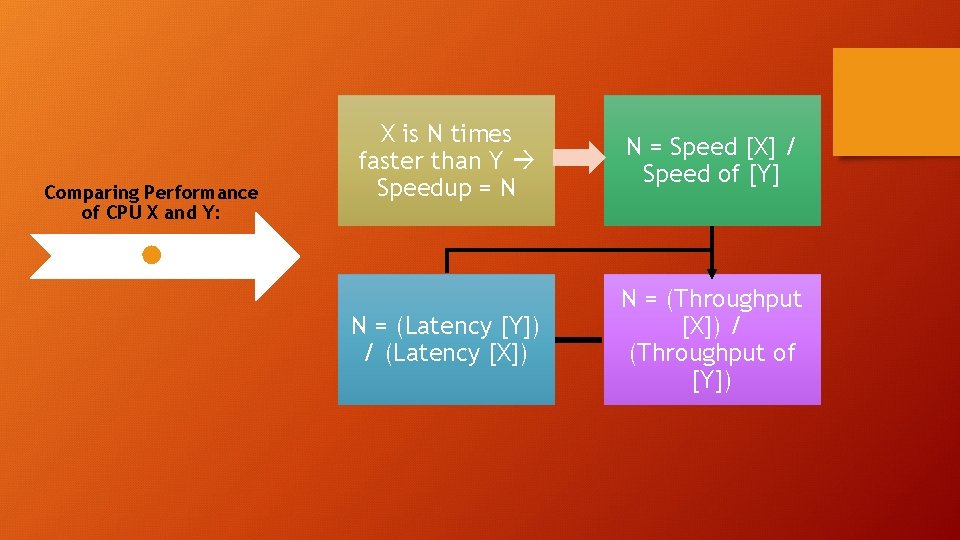
Comparing Performance of CPU X and Y: X is N times faster than Y Speedup = N N = Speed [X] / Speed of [Y] N = (Latency [Y]) / (Latency [X]) N = (Throughput [X]) / (Throughput of [Y])

Introduction to Caches:
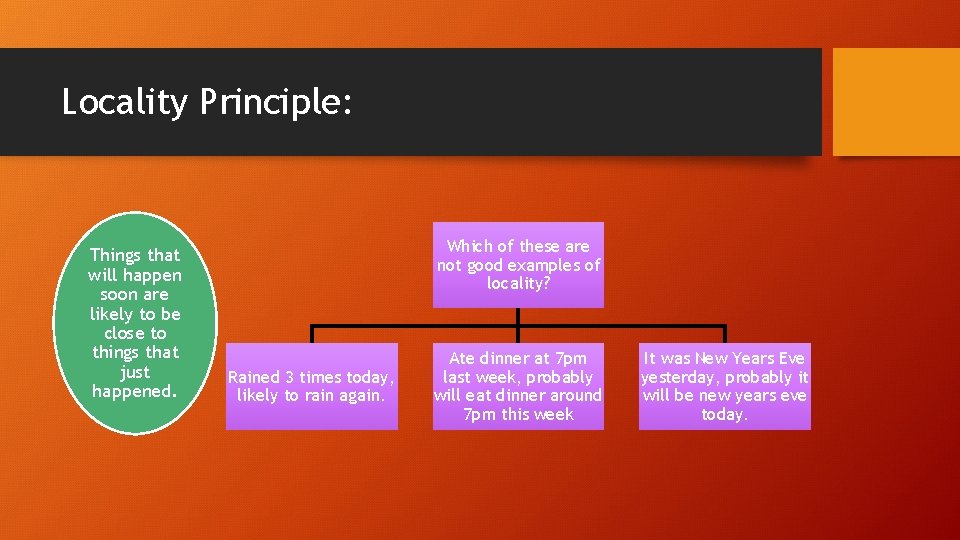
Locality Principle: Things that will happen soon are likely to be close to things that just happened. Which of these are not good examples of locality? Rained 3 times today, likely to rain again. Ate dinner at 7 pm last week, probably will eat dinner around 7 pm this week It was New Years Eve yesterday, probably it will be new years eve today.

Memory Locality:

Accessed Address X recently Likely to Access X again soon Likely to Access address close to X too

Temporal & Spatial Locality Implementation: for (j = 0; j < 1000 ; j++) print arr[j]

Locality to enhance Data Access: Library : Repository to store data, large but slow to access Library Accesses have temporal and spatial locality A student 1. Will go to library find information, go home (Does not benefit from locality) 2. Borrow the book 3. Take all books and build a library at home (Expensive and high latency)
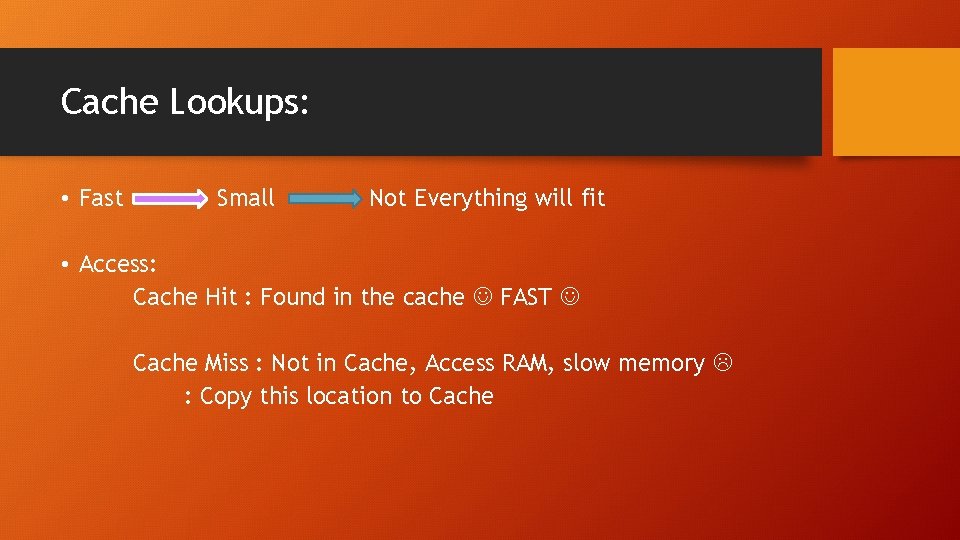
Cache Lookups: • Fast Small Not Everything will fit • Access: Cache Hit : Found in the cache FAST Cache Miss : Not in Cache, Access RAM, slow memory : Copy this location to Cache

Cache Performance: Average Memory Access Time (AMAT) AMAT = HIT TIME + MISS RATE x MISS PENALTY Hit Time Should be low; small and fast cache Miss Rate Should be low; large and/or smart cache Miss Penalty Main Memory Access Time, Large (10 -100 s cycles) MISS TIME = HIT TIME + MISS PENALTY (RAM Access time when Cache Miss)

Cache Size in Real Processors: Complication : Several Caches in the Processor L 1 Cache Directly service all RD/WR requests from Processor Size: 16 -64 KB • Large enough to get ~ 90% hit rate • Small enough to hit in 1 – 3 cycles

Cache Organization: • How to determine HIT or MISS ? • How to determine what to kick out ? Address from Data HIT DATA (Bytes in each entry) Block Size / Line Size 32 to 128 bytes Block size can’t be as large as 1 KB, as precious Cache memory will remain unused. Has to be large enough to satisfy spatial locality, if more than 1 block needs to be replaced when cache miss.
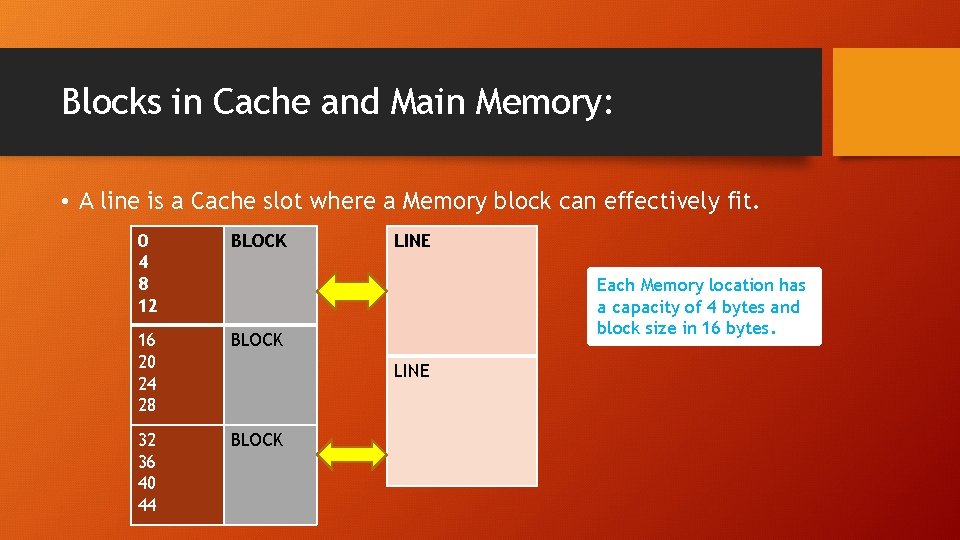
Blocks in Cache and Main Memory: • A line is a Cache slot where a Memory block can effectively fit. 0 4 8 12 BLOCK 16 20 24 28 BLOCK 32 36 40 44 BLOCK LINE Each Memory location has a capacity of 4 bytes and block size in 16 bytes. LINE
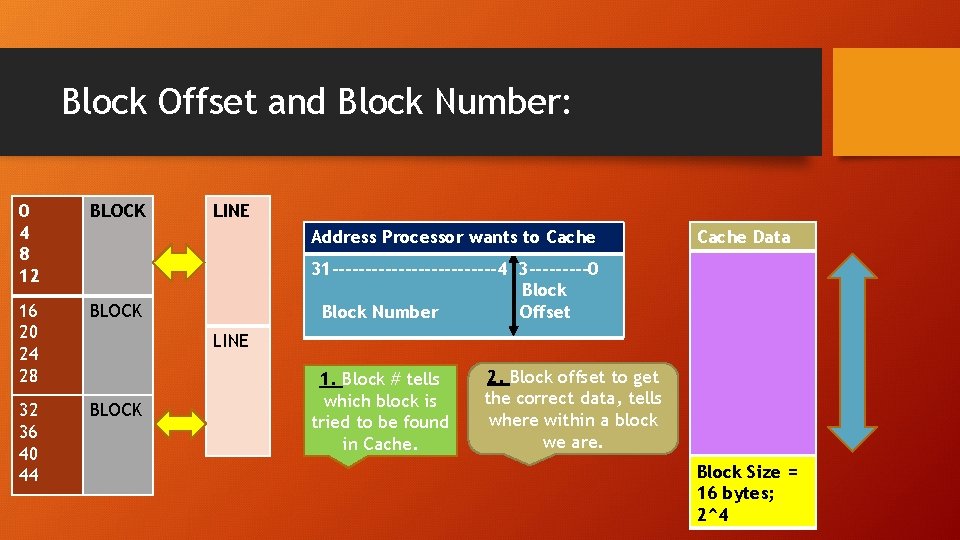
Block Offset and Block Number: 0 4 8 12 BLOCK 16 20 24 28 BLOCK 32 36 40 44 BLOCK LINE Address Processor wants to Cache Data 31 -------------4 3 -----0 Block Number Offset LINE 1. Block # tells which block is tried to be found in Cache. 2. Block offset to get the correct data, tells where within a block we are. Block Size = 16 bytes; 2^4

Cache Block Number Quiz: 32 Byte Block Size 16 bit address created by the Processor 1111 0000 1010 0101 What is the block number corresponding to the above address? What is the block offset?
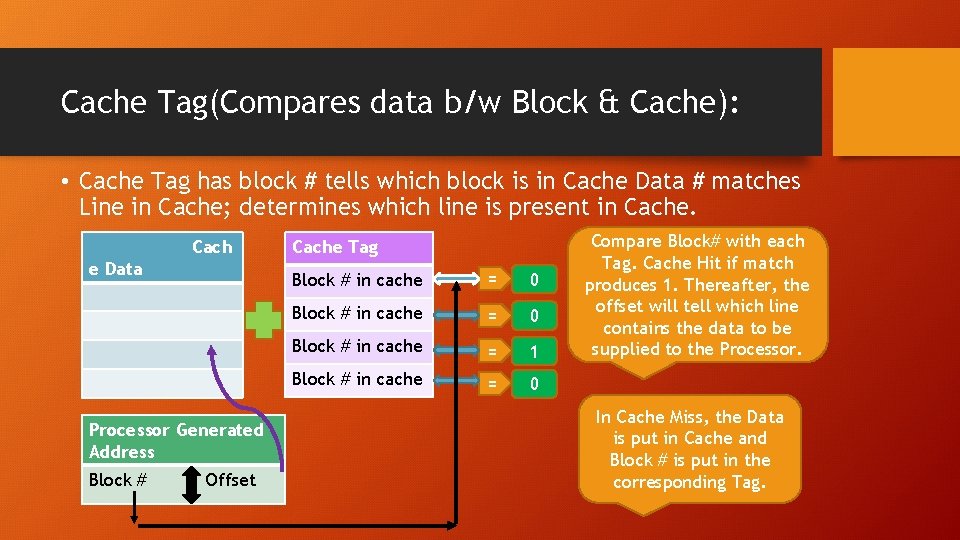
Cache Tag(Compares data b/w Block & Cache): • Cache Tag has block # tells which block is in Cache Data # matches Line in Cache; determines which line is present in Cache. Cach e Data Processor Generated Address Block # Offset Cache Tag Block # in cache = 0 Block # in cache = 1 Block # in cache = 0 Compare Block# with each Tag. Cache Hit if match produces 1. Thereafter, the offset will tell which line contains the data to be supplied to the Processor. In Cache Miss, the Data is put in Cache and Block # is put in the corresponding Tag.

Valid Bit: • During Boot up, no data from Cache needed. Garbage Data accessed if Memory Block and TAG match. Cache Data Cache TAG VALID Garbage Data not brought from RAM. 000000 (Initial) 0 0 Any initial value at the Cache Tag will be problematic, not just zero. Therefore Valid bit = 0 0 0 X 0000 001 C Hit (Tag == Block#) and Valid = 1

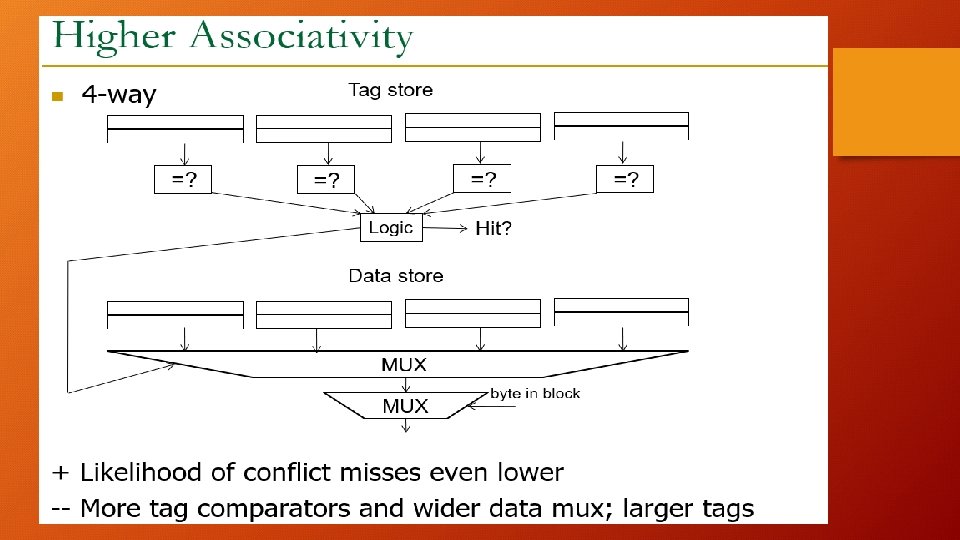
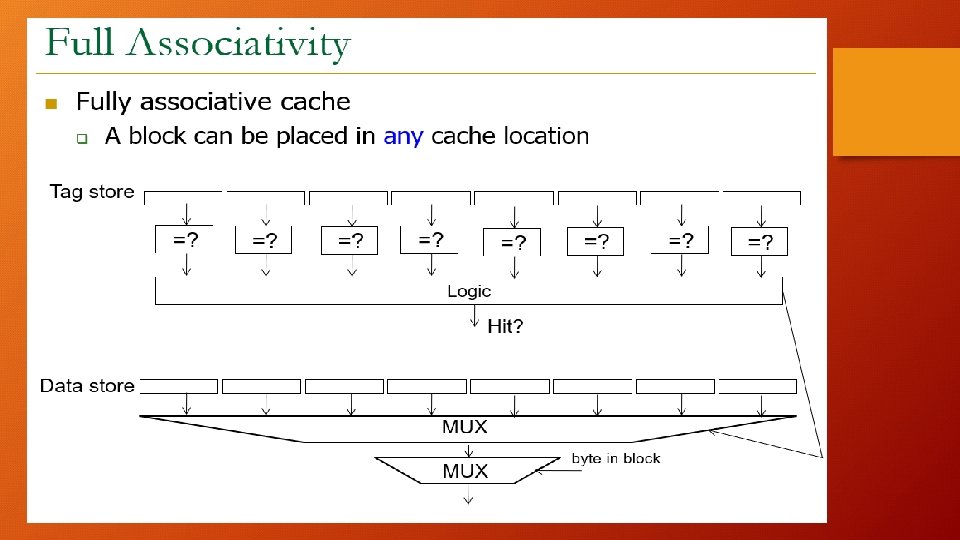
Types of Caches: Fully Associative: Any block can be in any Cache Line, N lines with N comparisons (Extreme flexible form of Set Associative) Set Associative: N Lines where a block can be (Middle Ground) Direct Mapped: A block can go into 1 line (Extreme rigid form of Set Associative)
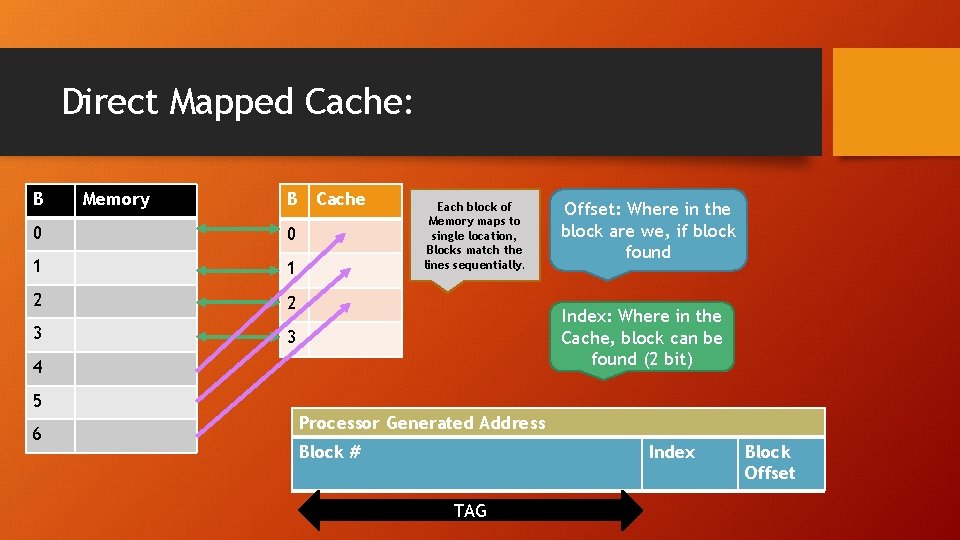
Direct Mapped Cache: B Memory B Cache 0 0 1 1 2 2 3 3 Each block of Memory maps to single location, Blocks match the lines sequentially. Offset: Where in the block are we, if block found Index: Where in the Cache, block can be found (2 bit) 4 5 6 Processor Generated Address Block # Index TAG Block Offset

Adv. /Disadvantages of Direct Mapped Cache: Looks only in one place, 1: 1 mapping: Fast: Since one location checked, less traffic, Hit Time (good) Cheap: Less complex design, one tag and valid bit comparator Energy Efficient: Lesser Power Dissipation due to smaller design Blocks must go in one place: Frequent accesses to A B which map to same place in cache (Line) Simultaneous kicking out of A & B. Conflict over one spot Therefore, a high miss rate
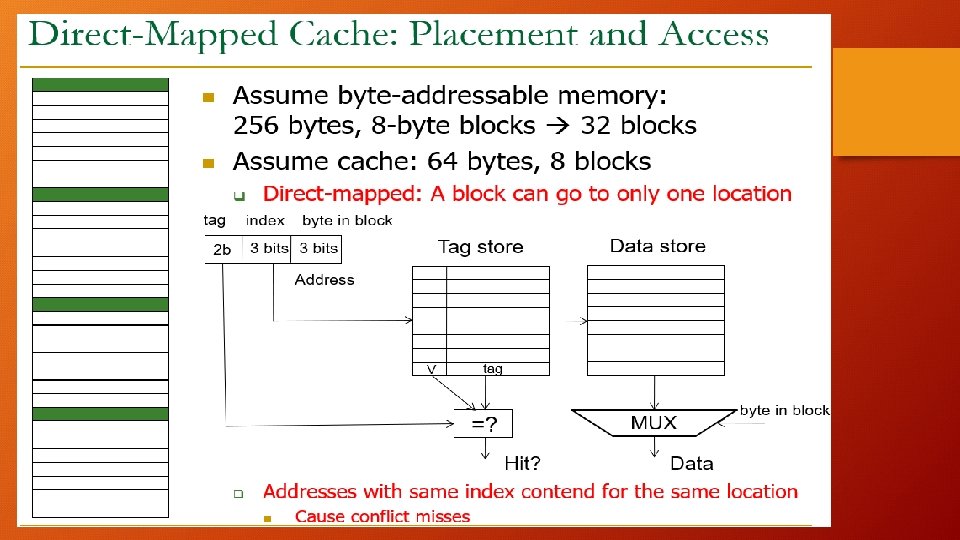

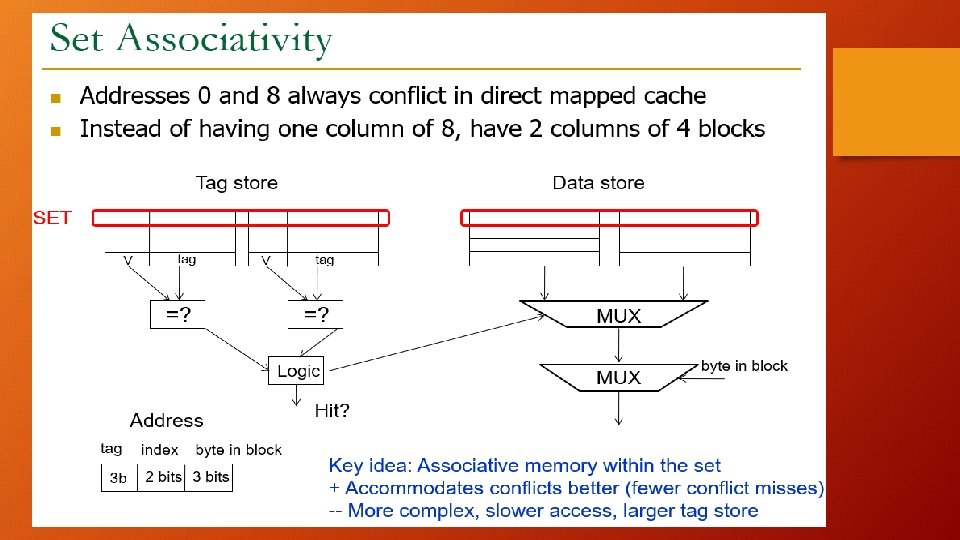
Set Associative Caches: • N – Way Set Associative Block can be in one of N lines in any SET 0 Line 1 SET 1 Line 2 Line 3 SET 2 Line 4 Line 5 SET 3 Line 6 Line 7 2 Way Set Associative, N = 2, 2 lines / block Within a set, there are 2 lines which can contain the block Few bits of block address allocated for which set the block will go

Offset, Index Tag for Set Associative Caches: SET 0 Line 0 TAG INDEX OFFSET Line 1 SET 1 Determines which set to access (2 bits) Line 2 Line 3 SET 2 Line 4 Line 5 SET 3 Line 6 Line 7 Direct Mapped Cache of the same size will have a smaller TAG ? Where in the block we are

Fully Associative Cache: • No index bits, as destination can be in any of the cache. TAG Offset Line 0 Line 1 Line 2 Line 3 Line 4 Line 5

Cache Summary: • Direct Mapped 1 Way Set Associative • Fully Associative N Way Set Associative, N = # of lines, no sets TAG INDEX Index = log 2(sets) OFFSET Offset = log 2(block size)

Cache Replacement: Cache Miss during a full set Need a new block in set Which block to kick out? Random FIFO: Kick out which has been in the longest LRU : Kick out block not been used for the longest

Implementing LRU : Implements Locality Block TAG VALID LRU Counter A 0 3 2 1 0 B 1 0 3 2 1 C 2 1 0 3 2 D 3 2 1 0 3 E 3 2 1 1 B 0 3 2 3 C 1 0 0 0 D 2 1 3 2 Maintaining count is complicated. For N – way set associative Cache, we have N counters with size log 2(N) – bit Counters. Here we have 4, 2–bit counters to count from 0 to 3. Cost: N log 2(N) Counters Energy: Change N Counters on each access (even Cache hits)

Write Policy of Caches: Do we insert blocks we write (Write Miss)/Allocate Policy ? Write Allocate: Bring block into cache (helps locality RD/WR) No Write Allocate: Do not bring block into cache when written. Do we write just to Cache or also to Memory ? (Cache Hit) Write Through: Update Memory immediately Write Back: Write to Cache, only write to RAM when Cache block replaced (High Locality WR will only update Cache frequently)

Write Back Caches: Blocks we did write, when replaced Write to Memory (RAM) Blocks we didn’t write, when replaced No need to write to RAM Multiple Writes on Read inefficient / Efficient implementation? Add a dirty bit to Cache Dirty Bit 0 Block is clean (not written since brought from RAM) Dirty Bit 1 Block is dirty (need to write back on replacement)
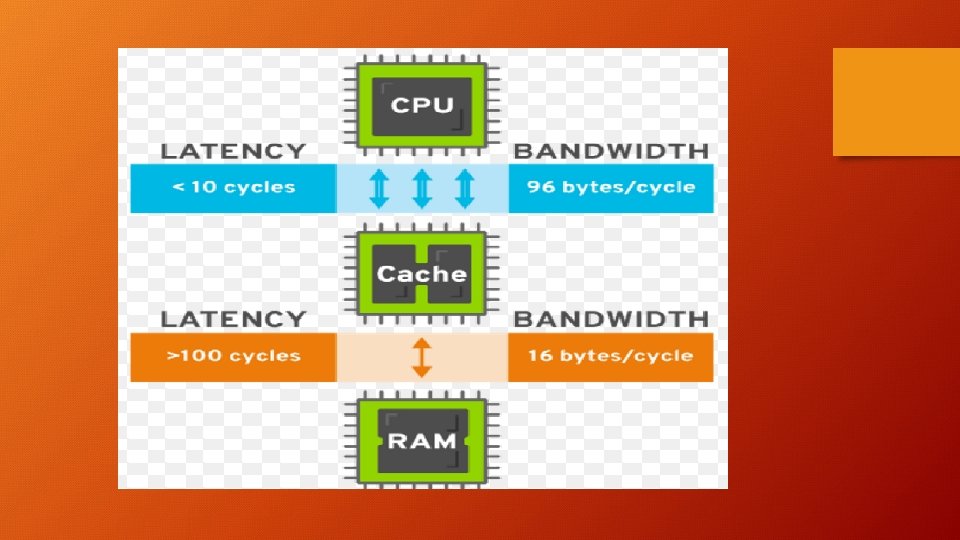

Multi-Level Caches (Cache Hierarchy):

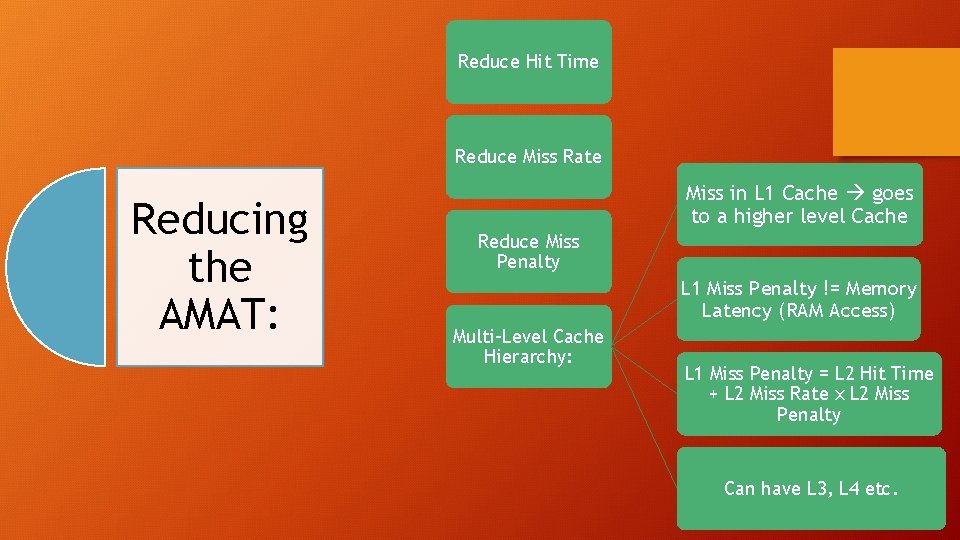
Reduce Hit Time Reduce Miss Rate Reducing the AMAT: Miss in L 1 Cache goes to a higher level Cache Reduce Miss Penalty L 1 Miss Penalty != Memory Latency (RAM Access) Multi-Level Cache Hierarchy: L 1 Miss Penalty = L 2 Hit Time + L 2 Miss Rate x L 2 Miss Penalty Can have L 3, L 4 etc.

AMAT = L 1 Hit Time + L 1 Miss Rate x L 1 Miss Penalty AMAT with Cache Hierarchies: L 1 Miss Penalty = L 2 Hit Time + L 2 Miss Rate x L 2 Miss Penalty = L 3 Hit Time + L 3 Miss Rate x L 3 Miss Penalty LLC Miss Penalty = Main Memory Latency
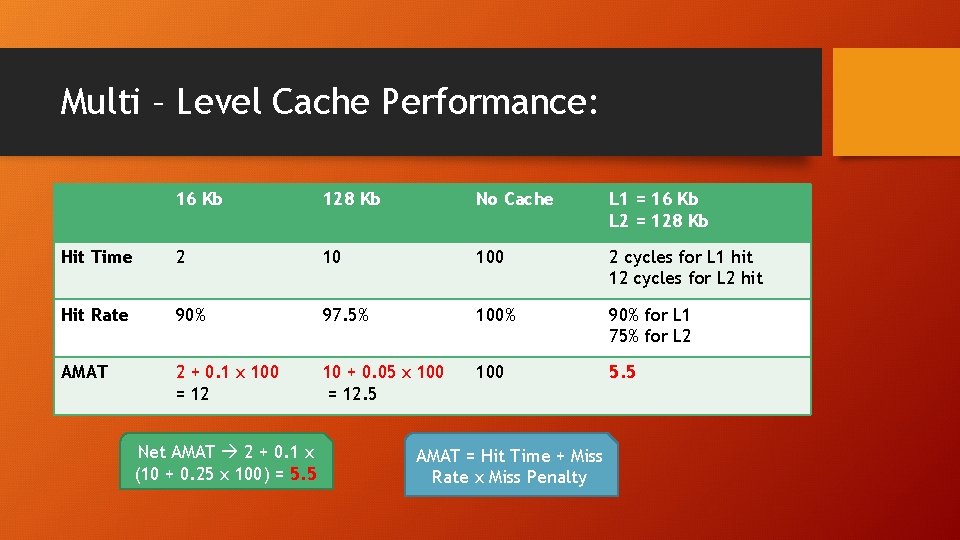
Multi – Level Cache Performance: 16 Kb 128 Kb No Cache L 1 = 16 Kb L 2 = 128 Kb Hit Time 2 10 100 2 cycles for L 1 hit 12 cycles for L 2 hit Hit Rate 90% 97. 5% 100% 90% for L 1 75% for L 2 AMAT 2 + 0. 1 x 100 = 12 10 + 0. 05 x 100 = 12. 5 100 5. 5 Net AMAT 2 + 0. 1 x (10 + 0. 25 x 100) = 5. 5 AMAT = Hit Time + Miss Rate x Miss Penalty

Hit Rate in L 1/L 2 Cache: 16 Kb 128 Kb No Cache L 1 = 16 Kb L 2 = 128 Kb Hit Time 2 10 100 2 cycles for L 1 hit 12 cycles for L 2 hit Hit Rate 90% 97. 5% 100% 90% for L 1 75% for L 2 AMAT 2 + 0. 1 x 100 = 12 10 + 0. 05 x 100 = 12. 5 100 5. 5 Global Hit Rate Local Hit Rate

Global Hit Rate 1 – Global Miss Rate Global vs Local Hit Rate: Global Miss Rate No. of misses in this Cache / No of All Memory Accesses Local Hit Rate No. of hits / No. of accesses to this Cache Misses per 1000 instructions (MPKI)

Inclusion Property in Caches: Assuming Block in L 1 -Cache May or may not be in L 2 – Cache Has to be in L 2 – Cache Inclusion Cannot be in L 2 – Cache Exclusion Misses from L 1 Cache May or may not be in L 2 – Cache, unless specified as Inclusion/Exclusion
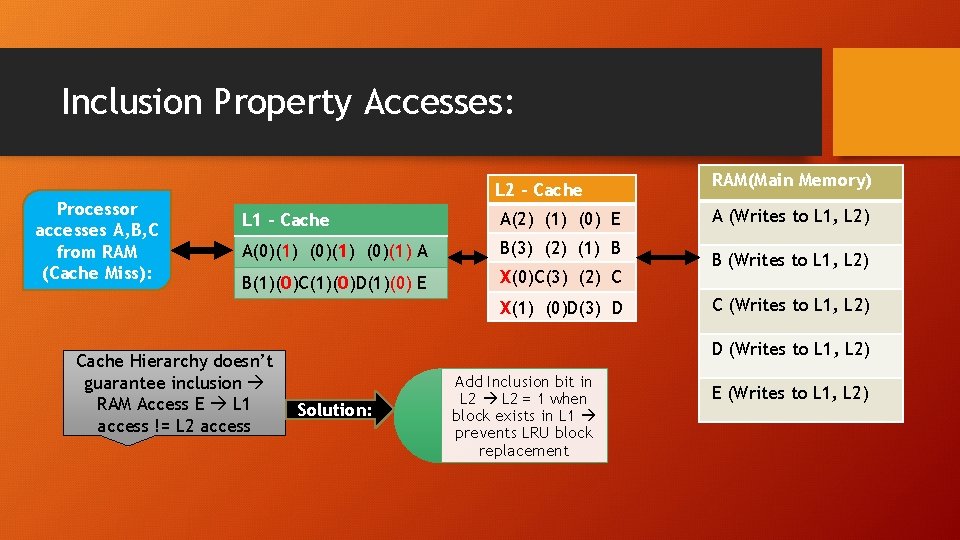
Inclusion Property Accesses: Processor accesses A, B, C from RAM (Cache Miss): L 2 – Cache L 1 – Cache A(2) (1) (0) E A(0)(1) A B(3) (2) (1) B B(1)(0)C(1)(0)D(1)(0) E X(0)C(3) (2) C X(1) (0)D(3) D Cache Hierarchy doesn’t guarantee inclusion RAM Access E L 1 access != L 2 access RAM(Main Memory) A (Writes to L 1, L 2) B (Writes to L 1, L 2) C (Writes to L 1, L 2) D (Writes to L 1, L 2) Solution: Add Inclusion bit in L 2 = 1 when block exists in L 1 prevents LRU block replacement E (Writes to L 1, L 2)

Intel Montecito Chip:
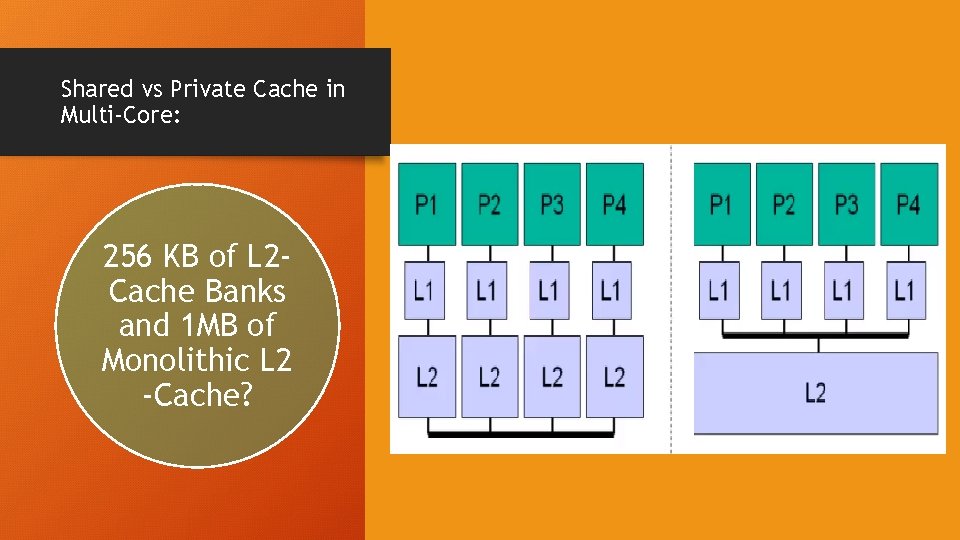
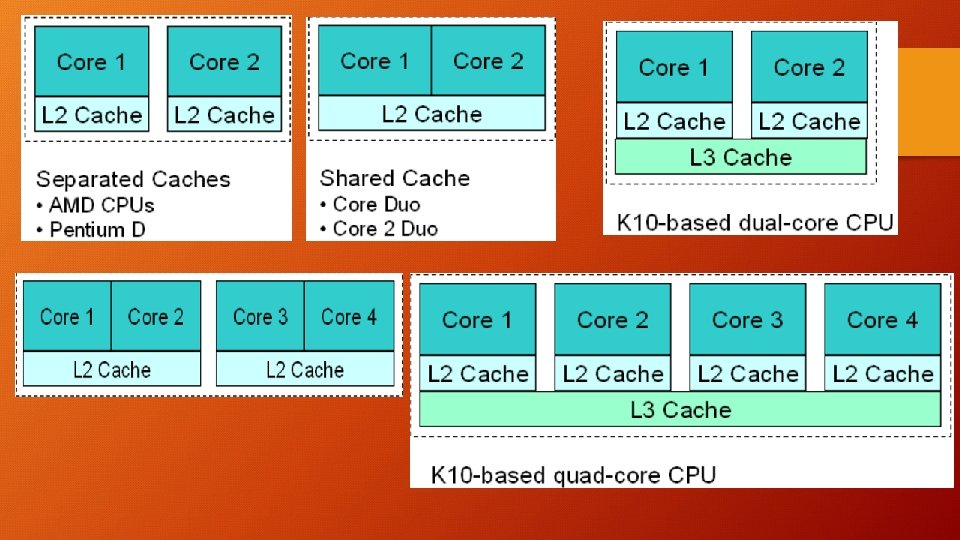
Shared vs Private Cache in Multi-Core: 256 KB of L 2 Cache Banks and 1 MB of Monolithic L 2 -Cache?

Why Private L 1 – Cache only? Shared L 1 Cache: Multiple Accesses on Multi-Core Creates too much traffic congestion Build Multi-Port Cache to reduce traffic. Single Cycle Access: If P 4 Accesses L 1 location higher Latency/Clock Cycles

Miss on L 2 Private != RAM, check other L 2 for latest value in Private L 2 Shared L 2 – Cache disadvantages: In Shared L 2 1 copy of A location Miss on L 2 RAM access; Congestion on shared L 2 -Bus Higher Latency More Wire Delay to Cache controller [20 cycles] Wait for Priority Requests from other Cores [20+5 cycles] vs [10 cycles] for Private L 2 - Cache

Shared L 2 – Cache Merits: Higher Hit Rates Private L 2 has duplicates (<1 MB capacity) A’s in multiple locations (Lower HR) Static Allocation in Private L 2, 256 KB/core, P 1[385 KB] > L 2[256] High MR, P 2[150 KB] < L 2[256 KB] Resources Under Utilized Dynamic Memory Allocation in shared L 2, Memory assigned as per requirements [Core Demands] Potential faster Cache Coherence (easier to locate data on miss)

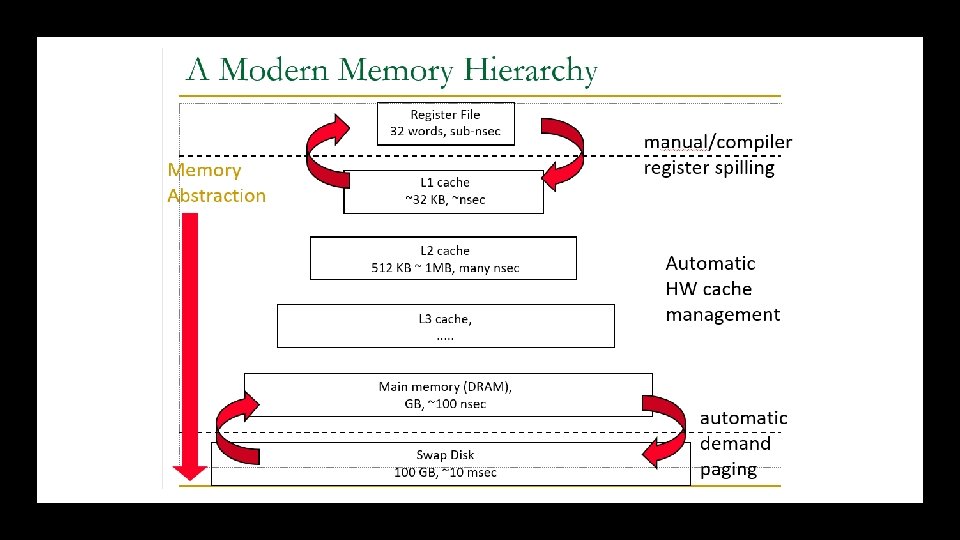
Memory in Modern Processor (L 1 Cache? ):
- Slides: 61