Basic Logic Gates Basic Logic Gates and Basic

Basic Logic Gates

Basic Logic Gates and Basic Digital Design • • • NOT, AND, and OR Gates NAND and NOR Gates De. Morgan’s Theorem Exclusive-OR (XOR) Gate Multiple-input Gates

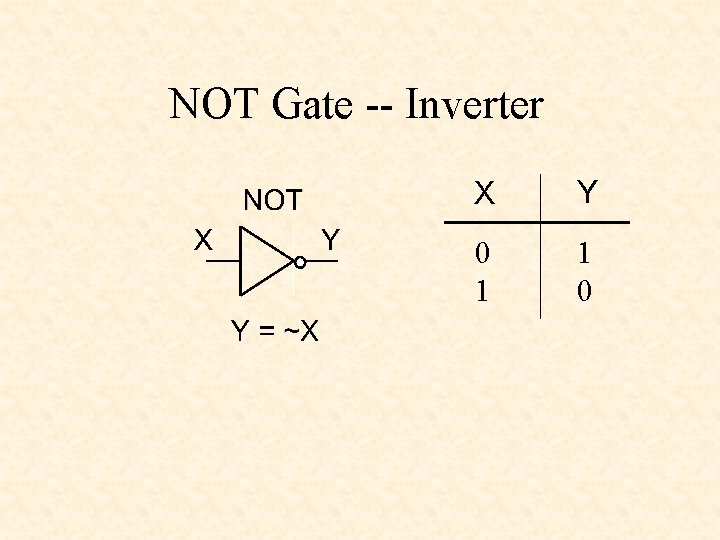
NOT Gate -- Inverter X Y 0 1 1 0

NOT • Y = ~X • Y = !X • Y = not X • Y = X’ • Y = X • not(Y, X) (Verilog) (ABEL) (VHDL) (textook) (Verilog)

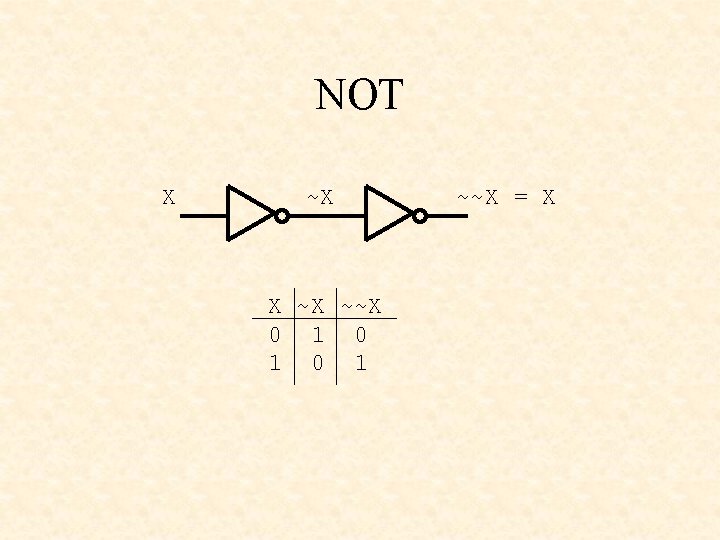
NOT X ~X ~~X 0 1 0 1 ~~X = X

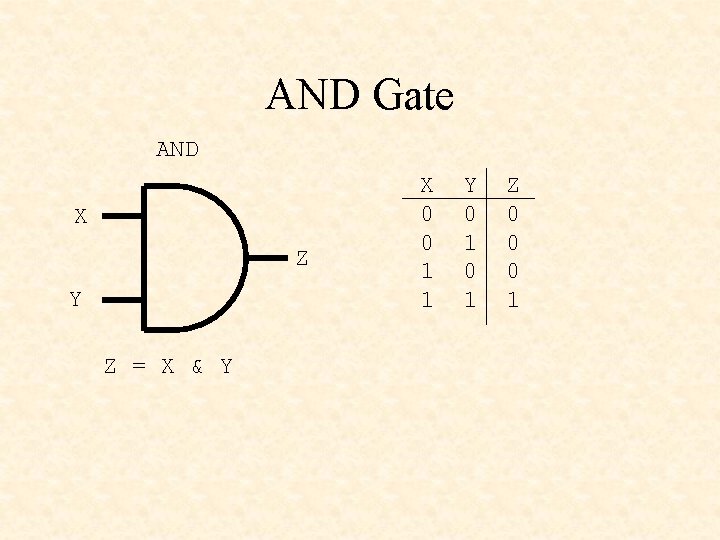
AND Gate AND X Z Y Z = X & Y X 0 0 1 1 Y 0 1 Z 0 0 0 1

AND • X & Y (Verilog and ABEL) • X and Y (VHDL) • X Y • X * Y • XY (textbook) • and(Z, X, Y) (Verilog) V U

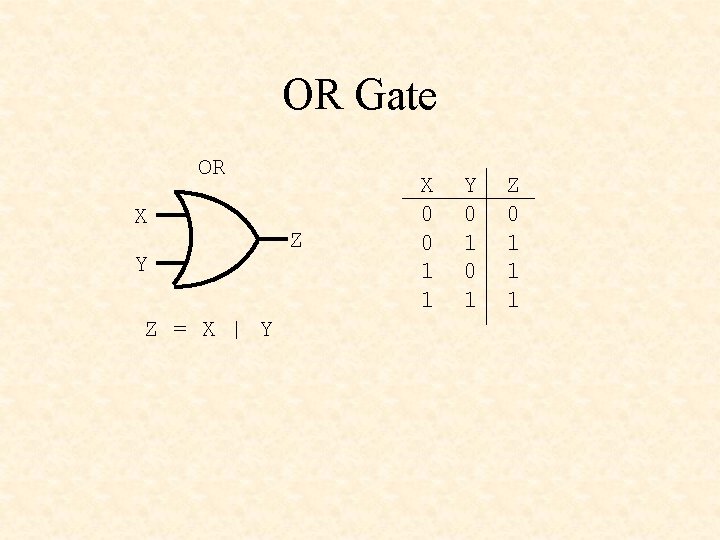
OR Gate OR X Y Z = X | Y Z X 0 0 1 1 Y 0 1 Z 0 1 1 1

OR • X | Y • X # Y • X or Y • X + Y • X V Y • X U Y • or(Z, X, Y) (Verilog) (ABEL) (VHDL) (textbook) (Verilog)

Basic Logic Gates and Basic Digital Design • • • NOT, AND, and OR Gates NAND and NOR Gates De. Morgan’s Theorem Exclusive-OR (XOR) Gate Multiple-input Gates

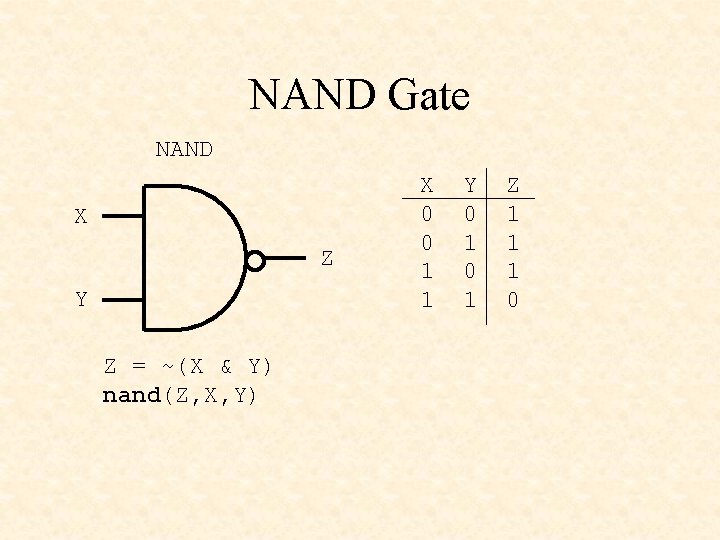
NAND Gate NAND X Z Y Z = ~(X & Y) nand(Z, X, Y) X 0 0 1 1 Y 0 1 Z 1 1 1 0

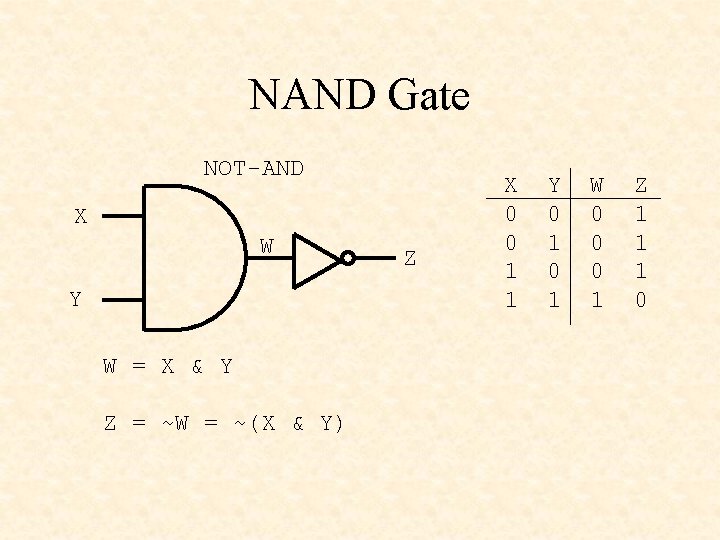
NAND Gate NOT-AND X W Y W = X & Y Z = ~W = ~(X & Y) Z X 0 0 1 1 Y 0 1 W 0 0 0 1 Z 1 1 1 0

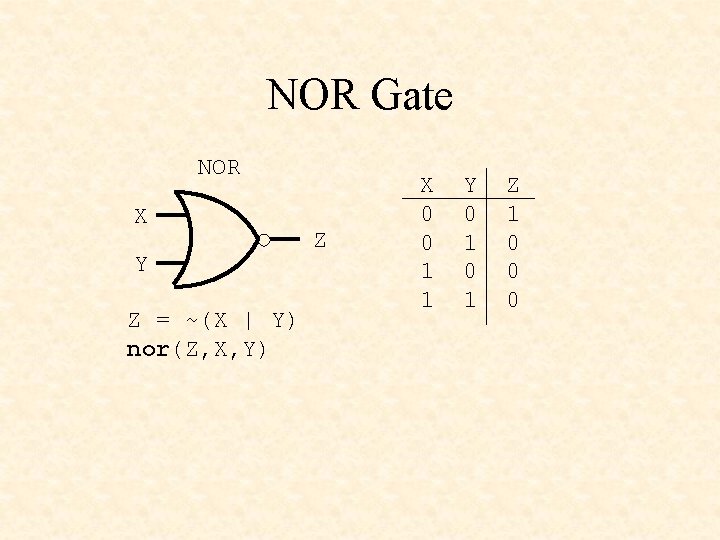
NOR Gate NOR X Y Z = ~(X | Y) nor(Z, X, Y) Z X 0 0 1 1 Y 0 1 Z 1 0 0 0

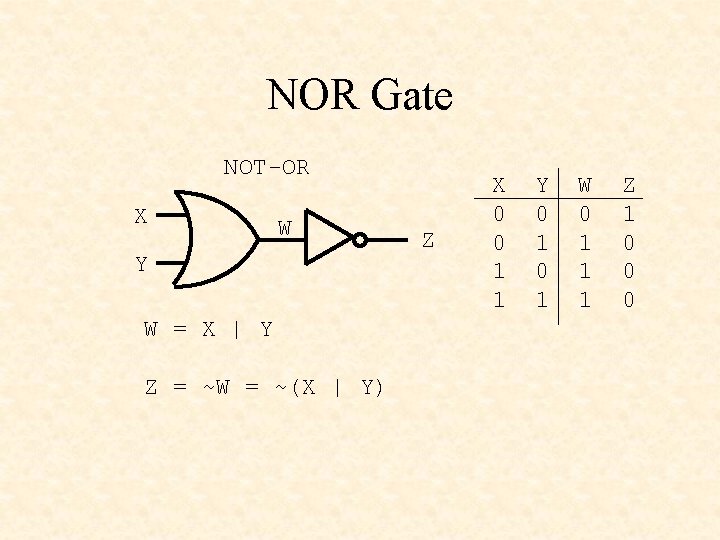
NOR Gate NOT-OR X W Y W = X | Y Z = ~W = ~(X | Y) Z X 0 0 1 1 Y 0 1 W 0 1 1 1 Z 1 0 0 0

Basic Logic Gates and Basic Digital Design • • • NOT, AND, and OR Gates NAND and NOR Gates De. Morgan’s Theorem Exclusive-OR (XOR) Gate Multiple-input Gates

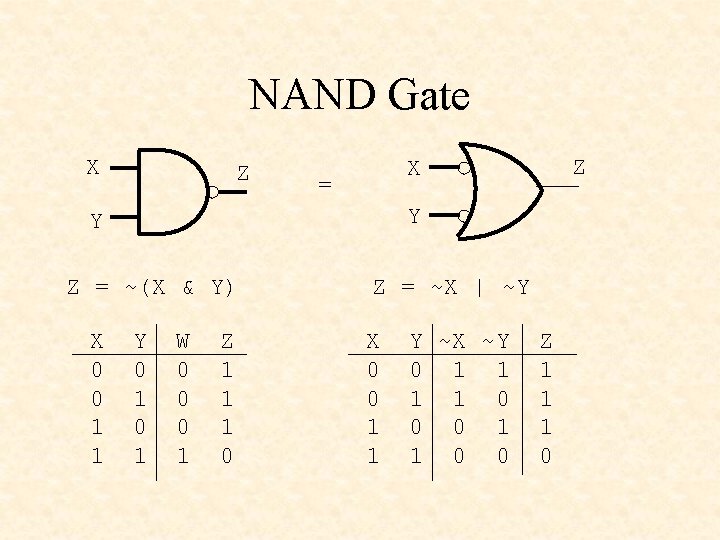
NAND Gate X Z = Y Y Z = ~(X & Y) X 0 0 1 1 Z X Y 0 1 W 0 0 0 1 Z 1 1 1 0 Z = ~X | ~Y X 0 0 1 1 Y ~X ~Y 0 1 1 0 0 Z 1 1 1 0

De Morgan’s Theorem-1 ~(X & Y) = ~X | ~Y NOT all variables • Change & to | and | to & • NOT the result •

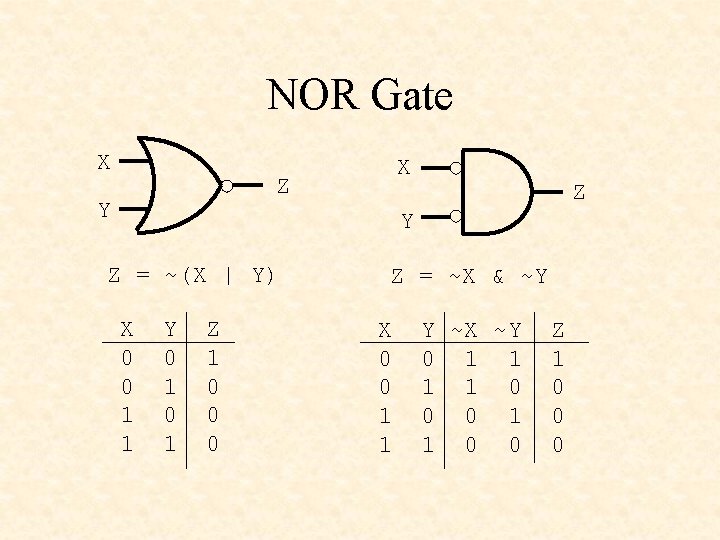
NOR Gate X X Z Y Z = ~(X | Y) X 0 0 1 1 Y 0 1 Z 1 0 0 0 Z = ~X & ~Y X 0 0 1 1 Y ~X ~Y 0 1 1 0 0 Z 1 0 0 0

De Morgan’s Theorem-2 ~(X | Y) = ~X & ~Y NOT all variables • Change & to | and | to & • NOT the result •

Basic Logic Gates and Basic Digital Design • • • NOT, AND, and OR Gates NAND and NOR Gates De. Morgan’s Theorem Exclusive-OR (XOR) Gate Multiple-input Gates

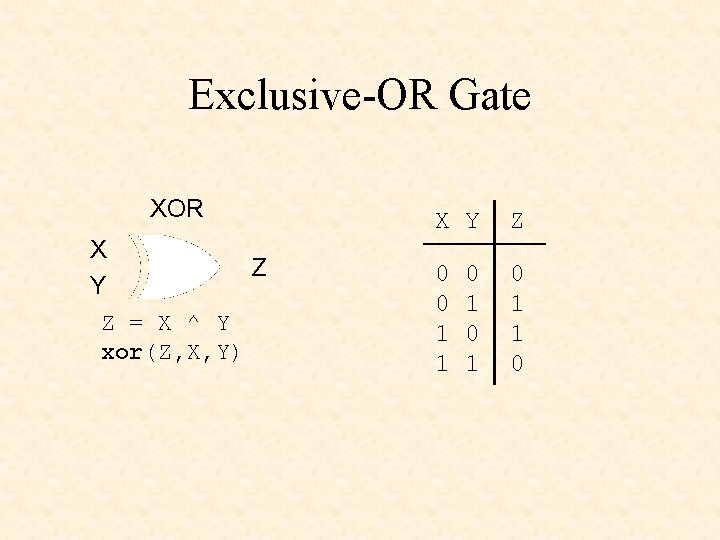
Exclusive-OR Gate XOR X Z Y Z = X ^ Y xor(Z, X, Y) X Y Z 0 0 1 1 0 0 1

XOR • X ^ Y • X $ Y • X @ Y (Verilog) (ABEL) • xor(Z, X, Y) (Verilog)

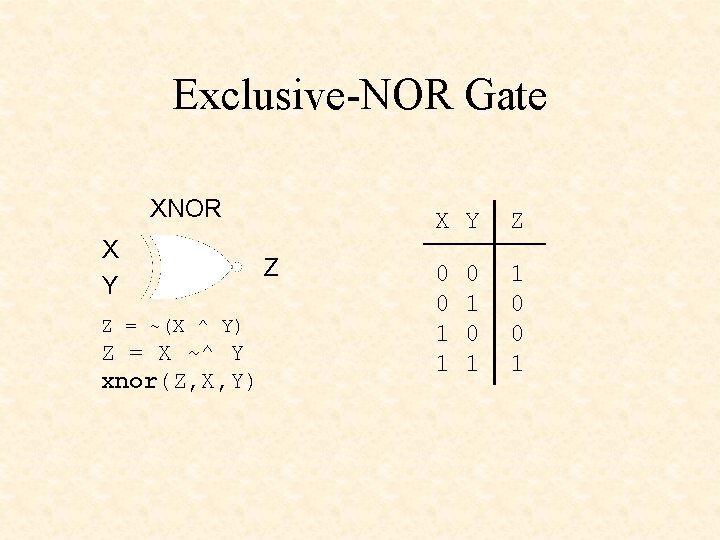
Exclusive-NOR Gate XNOR X Y Z = ~(X ^ Y) Z = X ~^ Y xnor(Z, X, Y) Z X Y Z 0 0 1 1 1 0 0 1 0 1

XNOR • X ~^ Y • !(X $ Y) • X @ Y (Verilog) (ABEL) • xnor(Z, X, Y) (Verilog)

Basic Logic Gates and Basic Digital Design • • • NOT, AND, and OR Gates NAND and NOR Gates De. Morgan’s Theorem Exclusive-OR (XOR) Gate Multiple-input Gates

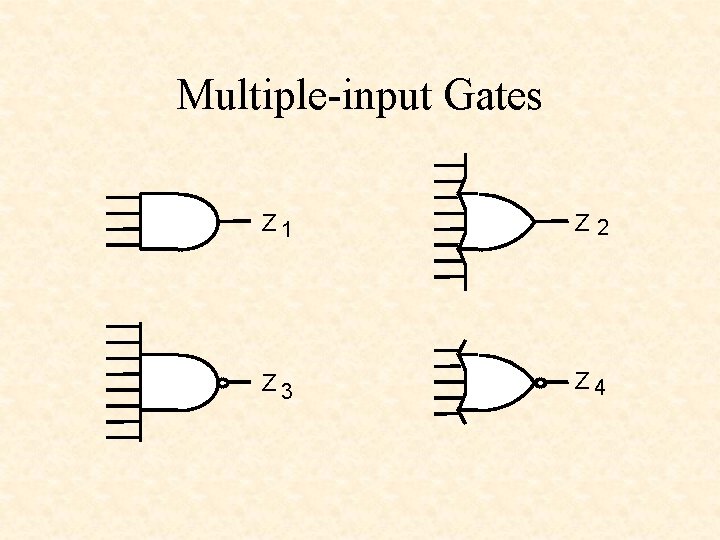
Multiple-input Gates Z 1 Z 2 Z 3 Z 4

Multiple-input AND Gate Z 1 Output Z 1 is HIGH only if all inputs are HIGH An open input will float HIGH

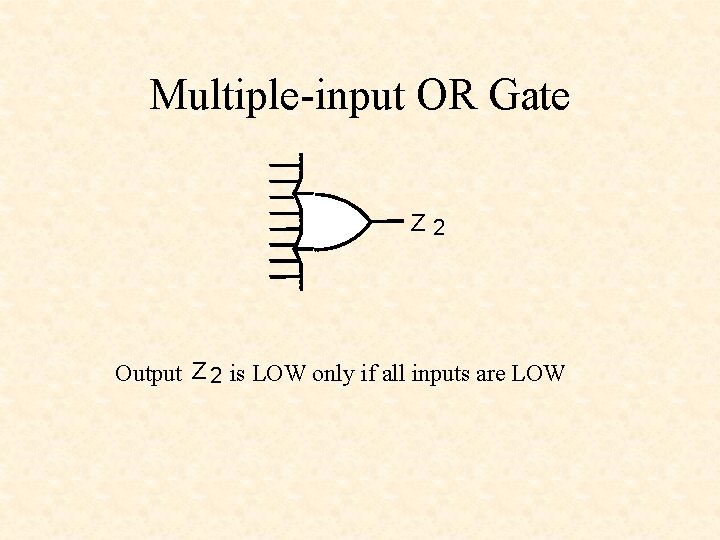
Multiple-input OR Gate Z 2 Output Z 2 is LOW only if all inputs are LOW

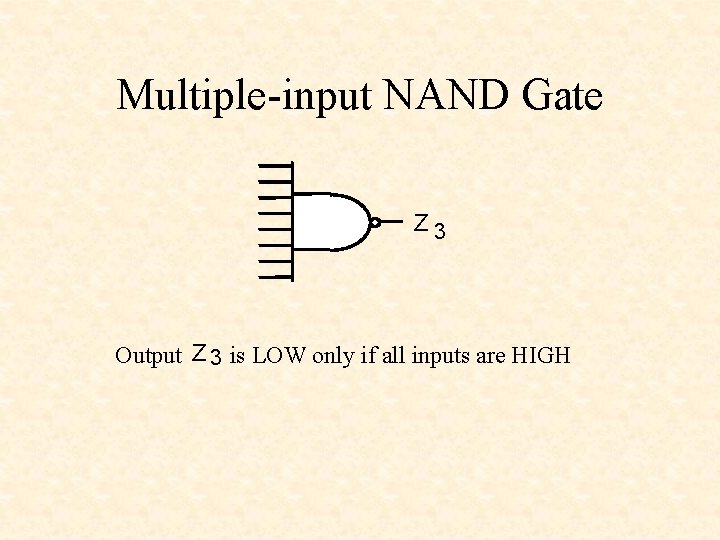
Multiple-input NAND Gate Z 3 Output Z 3 is LOW only if all inputs are HIGH

Multiple-input NOR Gate Z 4 Output Z 4 is HIGH only if all inputs are LOW